8.1.2  Hu不变矩

8.1.2 Hu不变矩

概率密度分布函数为f（x，y）的二维连续随机函数的（p+q）阶几何矩定义为

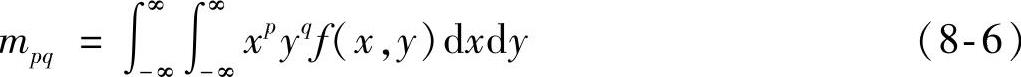
由式（8-6）可以看出，m_pq的值是由f（x，y）唯一确定的。由于m_pq不具备平移不变性，于是定义其（p+q）阶中心矩为

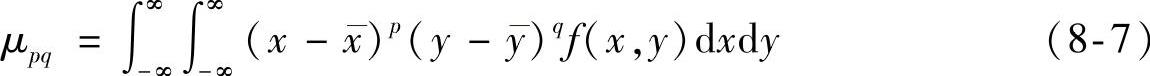
式中，。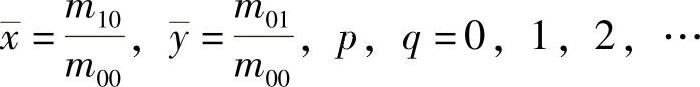

对于一幅大小为M×N的数字图像f（x，y），积分用求和代替，二维（p+q）阶几何矩和中心矩定义为

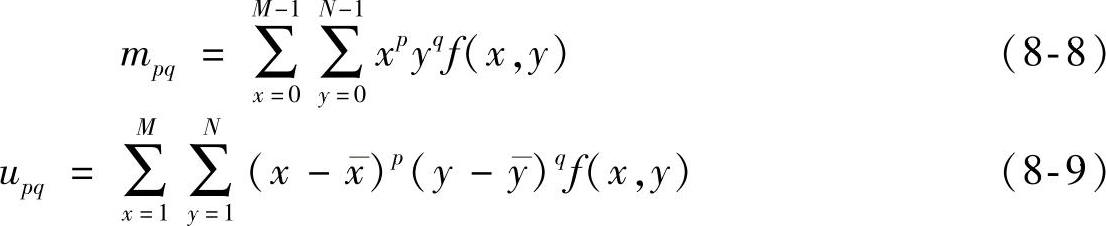
式中，p，q=0，1，2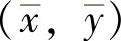，…，为灰度图像f（x，y）的灰度质心，定义为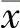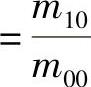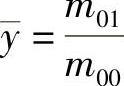，。归一化的中心矩，用η_pq表示，定义为

式中，

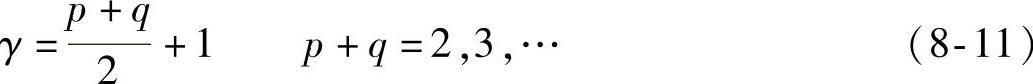
1962年，M.K.Hu利用归一化的二阶和三阶中心矩构造了七个不变矩，它们在连续图像条件下可保持平移、缩放和旋转不变性，具体定义如下：

ϕ₁=η₂₀^+η02（8-12）

ϕ₂=（η₂₀^-η02）2+4η²₁₁（8-13）

ϕ₃=（η₃₀^-3η12）2+（3η₂₁^-η03）2（8-14）

ϕ₄=（η₃₀+η₁₂）2+（η₂₁+η₀₃）2（8^-15）

ϕ₅=（η₃₀^-3η12）（η₃₀+η12）[（η₃₀+η12）2-3（η₂₁+η03）2]+（3η₂₁^-η03）

（η₂₁^+η03）[3（η₃₀+η₁₂）2-（η₂₁+η₀₃）2]

（8-16）

ϕ₆=（η₂₀^-η02）[（η₃₀+η12）2-（η21+η03）2]+4η₁₁（η30+η12）（η21+η03）

（8-17）

ϕ₇=（3η₂₁^-η03）（η₃₀+η₁2）[（η₃₀+η₁2）2-3（η₂₁+η₀₃）2]+（3η₁₂^-η30）

（η₂₁^+η03）[3（η₃₀+η₁₂）2-（η₂₁+η03）2]

（8-18）