4.3.1 全局阈值法
全局阈值法包含基于点的全局阈值法和基于区域的全局阈值法。其中基于点的全局阈值法是依据图像中每个点的灰度值确定阈值的;基于区域的全局阈值法是依据图像中邻域像素点的局部灰度值的分布来确定阈值的。基于点的全局阈值法包含直方图方法、最小误差法、矩量保持法以及最大熵方法等方法;基于区域的全局阈值法包含直方图变换法、概率松弛方法以及灰度分布统计方法等方法。
1.直方图方法
直方图方法的基本思想是依据待分割图像的灰度分布直方图来确定图像的阈值,包括p-分位数法(p-tile法)、双峰法以及直方图凹面分析法。
p-tile法是最早的灰度直方图的自动阈值分割方法,它依靠顺次积累灰度直方图的值来获取图像阈值。假设待分割图像中灰度级高的背景中存在一个灰度级低的目标,且已知目标在待分割图像中面积的比例为p,接着依次累计灰度直方图的值直到大于或等于p时,求得的灰度级就是图像的待求阈值。p-tile法计算相当简单,但是在使用该方法时必须预先知道目标在图像中的面积比p,如果p是未知的或随图像的不同发生变化,该方法就不能发挥分割作用了。
双峰法只适用于理想状态下目标和背景较清晰的图像,且此图像的灰度直方图呈双峰状分布,此时波谷与待分割图像的边缘相对应,因此当选取的阈值恰好是波谷的位置时,就可以获得较好的分割效果。但是,由于实际图像的情况一般来说较复杂,其图像的直方图参差不齐,分辨不出波峰、波谷,这个方法就不适用图像分割了。
直方图凹面分析法适用于直方图中没有波谷的图像。该方法中的凹面与直方图中的谷底和“肩”相对应,且在直方图的“肩”所处的位置上可以确定一个最佳阈值。但是由于原始灰度直方图往往会存在许多毛刺,使得该方法也不能准确定位直方图的“肩”所处的位置,从而导致产生错误的分割结果。
2.最小误差法
最小误差法的基本思想是将灰度直方图视为对其先验概率pi的正态分布的概率密度函数p(f)的估计,并假定图像中的目标和背景的灰度分布的均值是μi,方差是σi。p(f)的表达式见式(4-2),且最佳阈值可通过式(4-3)求得。
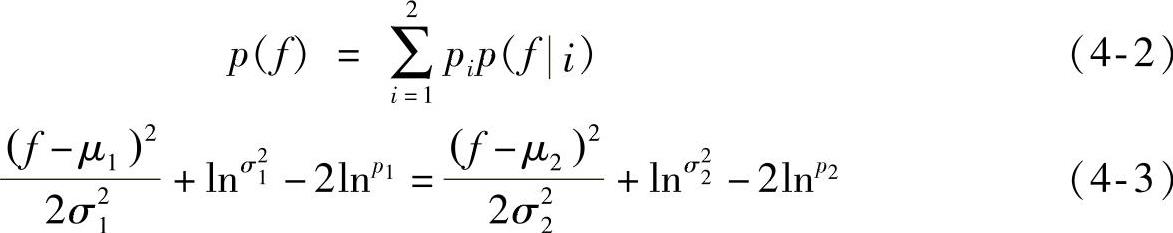
用此方法计算图像的阈值,需要知道统计参量σi、μi以及pi的值,但是这些值均是未知的,因此引入准则函数J(m),通过最小化准则函数J(m)求得最佳阈值T。其中J(m)的表达式见式(4-4),pi(m)的表达式见式(4-5),μi(m)的表达式见式(4-6),σi(m)的表达式见式(4-7)以及T的表达式见式(4-8)。
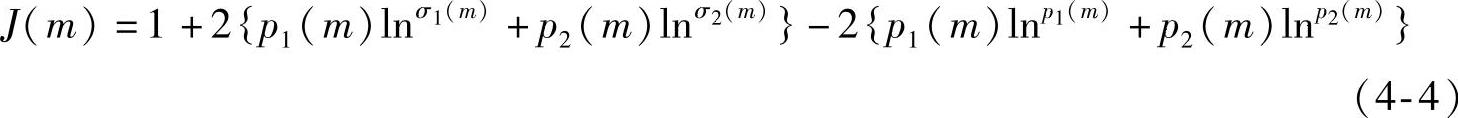
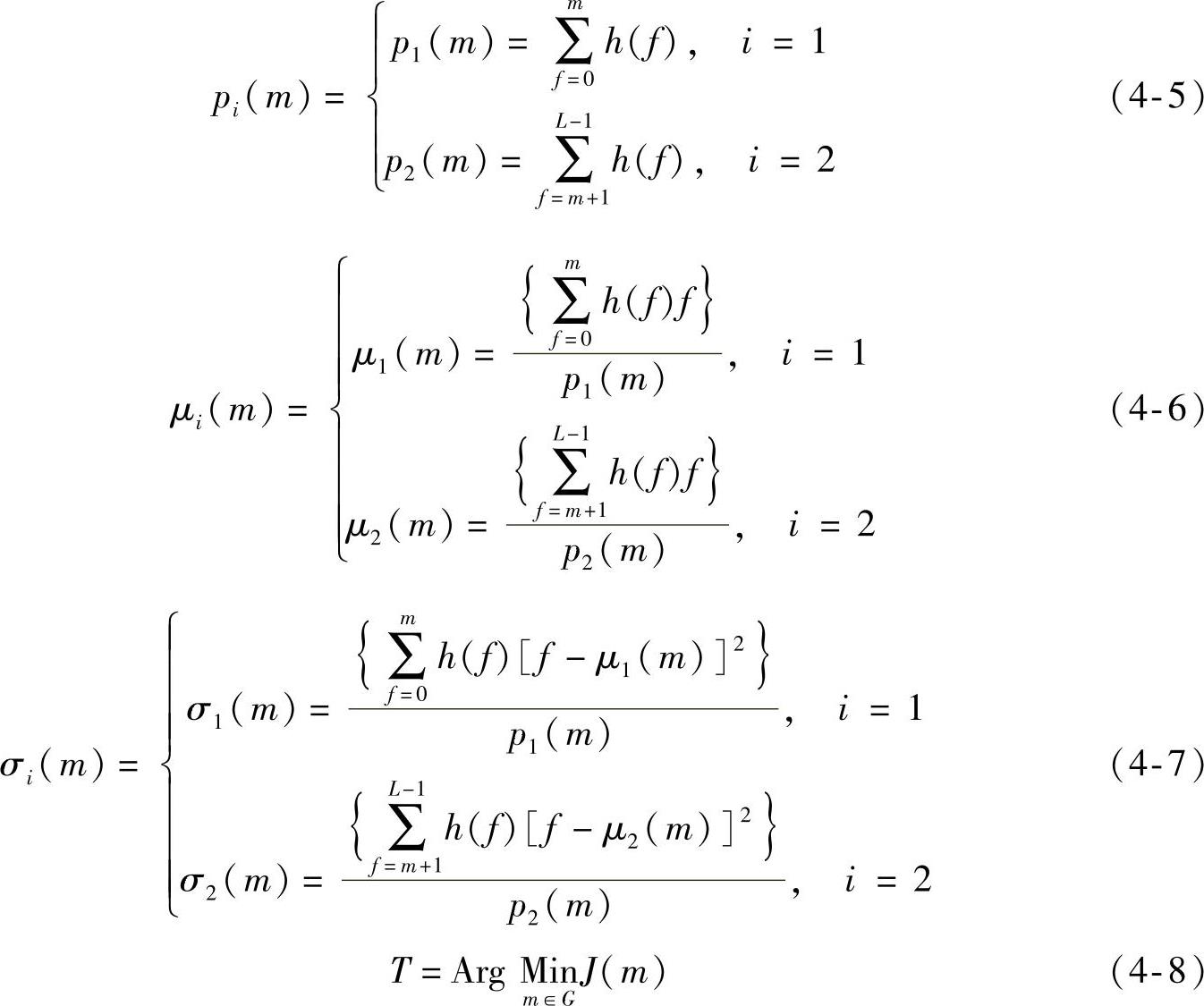
但是当图像中有多个目标和背景时,σi、μi以及pi的个数增多,计算量及计算难度都有所增加,因此该方法具有一定的局限性。
3.矩量保持法
矩量保持法又称矩守恒阈值法,即最优阈值在待分割图像和分割后的图像中的矩量保持恒定不变。若待分割图像的像素点的灰度值r∈{0,1,2,3,…,L-1},且L代表灰度级总数,Mi(i∈{0,1,2,3,…,L-1})代表灰度级i在待分割图像中出现的次数;pi代表灰度级i出现的频率,其表达式见式(4-9),nk代表第k阶矩,其表达式见式(4-10)。在此方法中,阈值分割应当满足前三阶矩恒定不变,其矩量保持方程见式(4-11),其中W0、W1分别代表阈值化后的每一个种别的灰度值,p0、p1表示阈值化后的灰度值的分布概率,通过求解方程组式(4-11),可以求出p0以及参数c0、c1、d,且其结果见式(4-12),此时求出的p0即为p0的分位数,也就是待分割图像的最优阈值T。
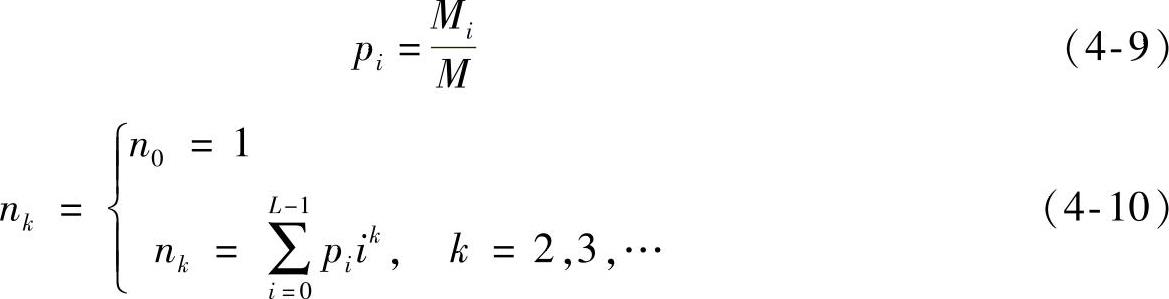
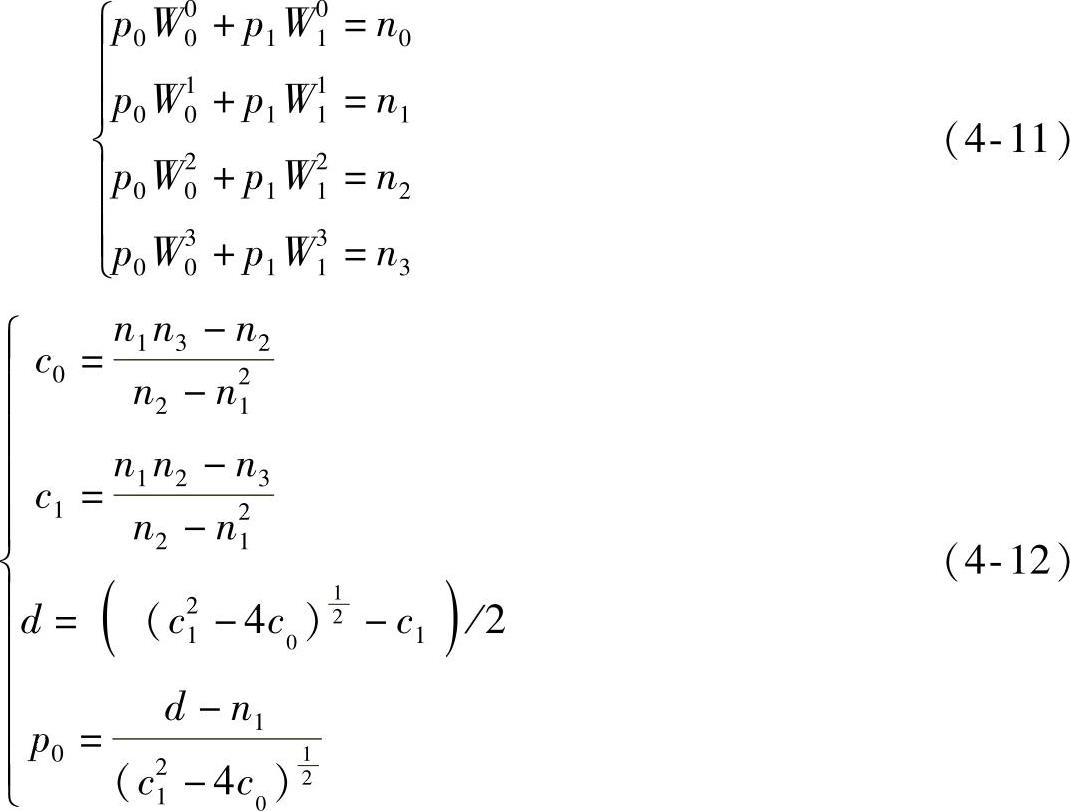
此方法是以理想状态下假设分割前与分割后的图像在矩量上保持恒定不变为前提的,但一般情况下由于图像受外界或自身复杂因素的影响,图像在分割后矩量均会有所变化,因此该方法不具有普遍性。
4.最大熵方法
最大熵方法是由Pun最早使用香农关于熵的概念提出的。该方法以图像完全由其灰度分布直方图表示为前提,用图像的熵作为度量实现对图像中的目标进行分割的目的。熵代表一个系统的信息量,记作H,其定义式见式(4-13),其中pr代表符号r出现的概率。因此对应定义图像的熵,pi代表图像中灰度级i出现的概率,其图像熵的表达式见式(4-14)。

图像阈值分割中应用熵的概念,其实质是通过研究灰度直方图熵的测量,从而寻找到图像的最优阈值,若熵的定义角度不同,那么就会有不同的最大熵方法。例如,如果考虑图像中灰度的空间分布,并通过像素的灰度值与其邻接像素的灰度均值来计算直方图,那么就会出现二维熵的阈值分割方法。较常用的最大熵方法有一维最大熵阈值法和二维最大熵阈值法。
一维最大熵阈值法的基本原理是假设灰度级T分割图像,将大于T的像素点的集合定义为背景N,且将小于T的像素点的集合定义为目标M;接着利用图像中目标和背景的灰度级的熵来计算图像的最大熵H,其表达式见式(4-15),其中,HN代表图像中背景的熵,其表达式见式(4-16);HM代表图像中目标的熵,其表达式见式(4-17);pN代表图像中背景所占面积的比例,其表达式见式(4-18);pM代表图像中目标所占面积的比例,其表达式见式(4-19);pi代表图像中灰度级i出现的概率。
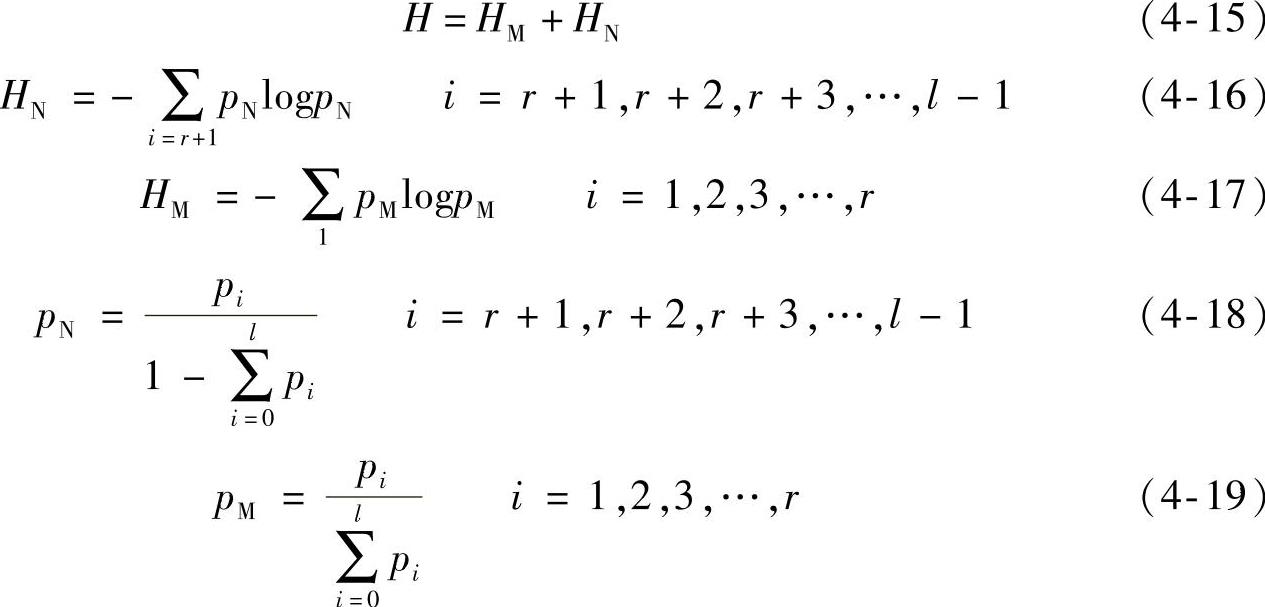
二维最大熵阈值法的基本原理与一维最大熵阈值法不同的是计算图像中灰度级的概率是用二维坐标表示的。例如,pij代表图像中像素点的灰度均值对(i,j)的概率,即图像中点的灰度为i,其区域灰度均值通过计算灰度为i的各个像素点及其八邻域像素点所组成区域的均值为j的概率。综上所述,当图像中的像素点变得相当多时,最大熵方法的计算量及计算难度都会有所增加,因此该方法也具有一定的局限性。
5.直方图变换法
直方图变换法的基本思想是依照图像中像素点的部分特征,将像素点加权后取得新的直方图而间接求取原图像的最佳阈值。因此,该方法取得最佳阈值的关键是要选取合适的加权方法以及最佳的权值。
6.概率松弛方法
概率松弛法的基本原理是假设图像是由较暗的目标和较亮的背景这两部分组成,并且用概率表示该图像中像素点及像素点之间的空间相关性,然后选择一个合适的阈值调整每个像素的概率,使得这个像素点只属于暗的目标区域或亮的背景区域,从而通过多次迭代使得图像中的目标与背景被明显地分割出来。该方法原理简单,但仅仅适用于待分割图像中的目标与背景灰度级分别处于直方图前后两半的情况。
7.灰度分布统计方法
灰度分布统计方法中一种典型的方法是灰度共生矩阵法。灰度共生矩阵中的元素是两个不同的灰度级在其相邻位置处出现的概率。该方法对应两个直方图,并且这两个直方图分别与灰度共生矩阵中的近对角线的元素、远对角线的元素相对应,那么该方法的最佳阈值就是在这两个直方图对应的波谷与波峰重叠的区域中获得。该方法在两个直方图对应的波谷与波峰不能重叠时失效,因而不能寻找到最佳阈值而无法完成图像分割的目的。
