7.2.1  协方差矩阵与协方差

7.2.1 协方差矩阵与协方差

存在一组随机变量为X₁，X₂，…，X_N，假设能够通过将上述的随机变量来随机地组成一组随机的向量X=[X₁，X₂，…，X_N]^T，在这组由随机变量构成的向量中，假设其中每个变量都有m个有效样本，这样就可以得到相应的样本矩阵：

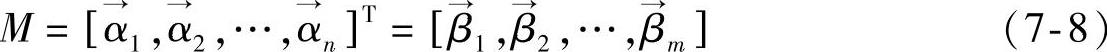
在式（7-8）中可以用矩阵参数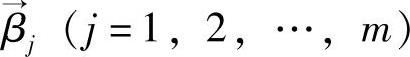来表示每个随机向量X中的样本向量，随机变量中样本所构成向量用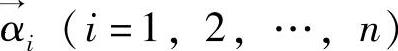来表示。

根据上述的随机变量X_i、X_j，可以将它们两者之间的协方差表示为

c_ij=E{[X_i-E（X_i）][X_j-E（X_j）]}（7-9）

通过已经给出的样本值，这样就能对它们的协方差进行有效的估计，得到的估计值如下：

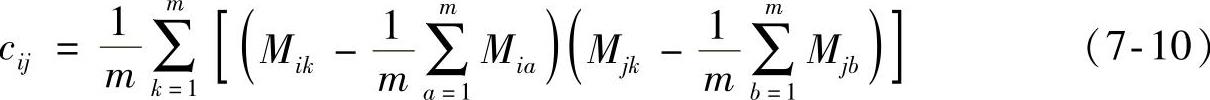
对式（7-10）进一步进行化简为

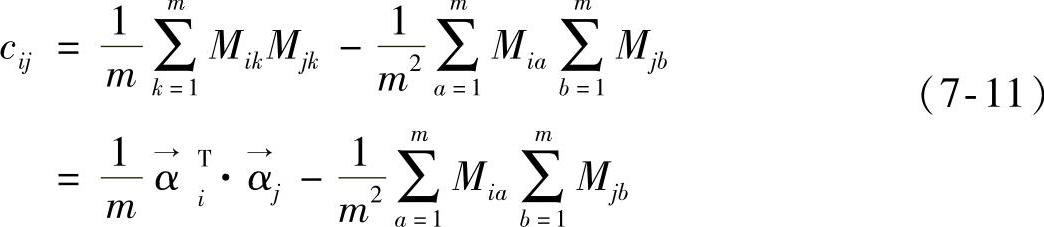
此时，我们所需要的协方差矩阵就能够表示如下：

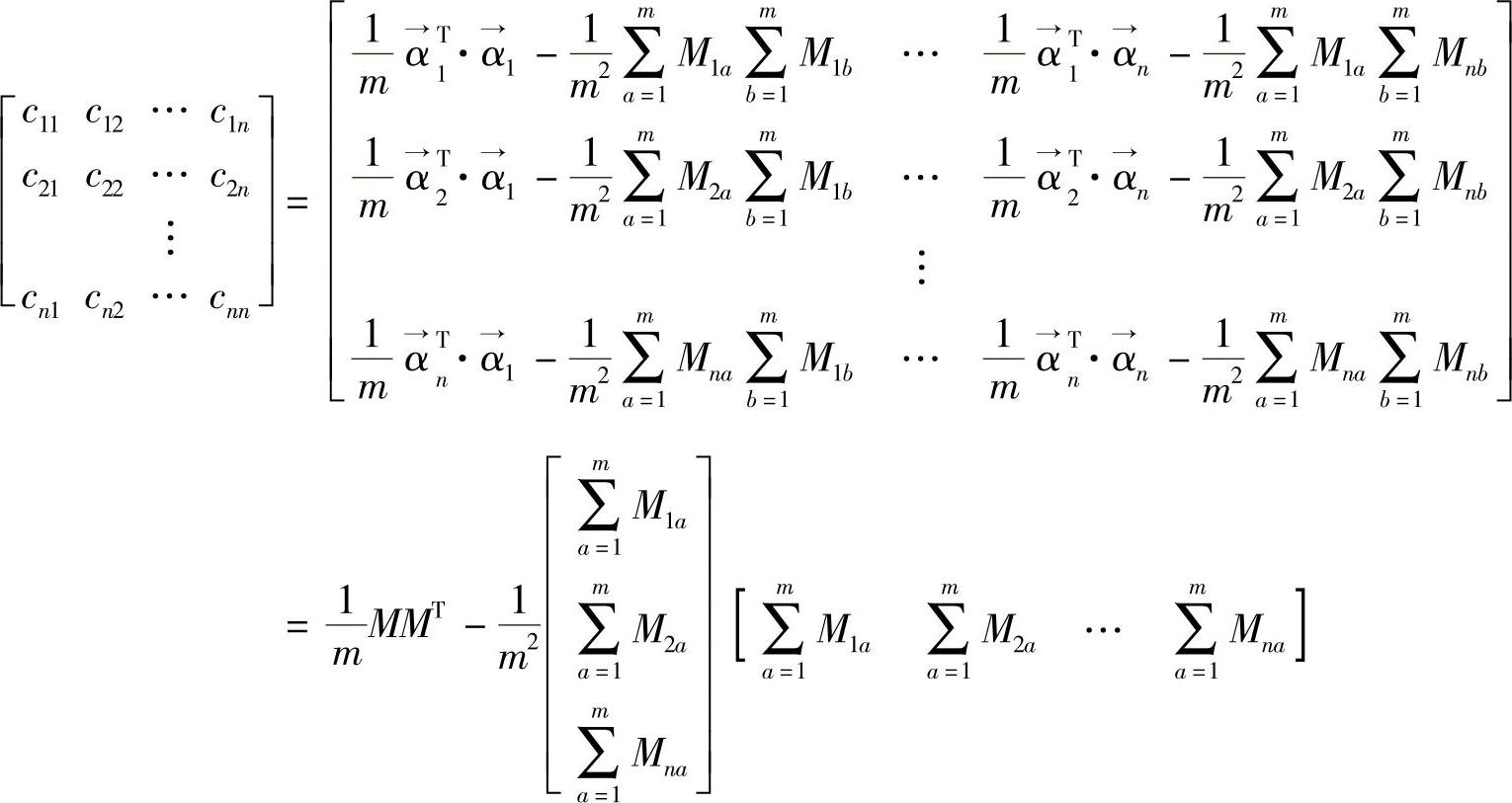
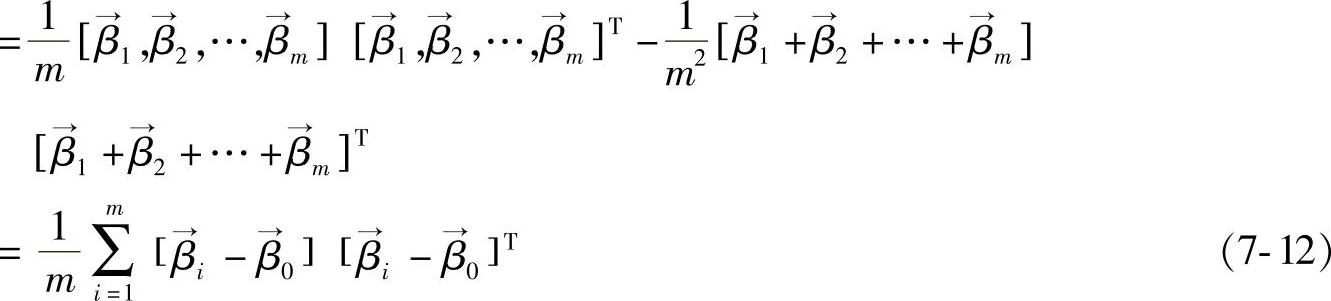
式中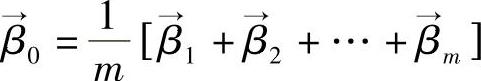，，由式（7-12）可对其进行进一步化简，最后我们可以得到相应的最简式，即我们所需要的协方差矩阵的表达式。

如果其所有样本存在平均值为零向量，那么式（7-12）就能够进一步化简为

根据上述对协方差和协方差矩阵的推导和对其值进行有效的估计，我们必须清楚地知道根据公式推导得到的协方差的真实值只是一个估计值，它是依靠大量的样本数据得到的估计值，如果我们的样本数据越多，样本在整体中的占比就会越大，最后获得的协方差矩阵就会越可靠。

在协方差矩阵中，每个变量都是随机向量X分量间不同的协方差，这里的协方差不是样本之间的协方差，在协方差矩阵如果用c_ij来表示矩阵中的元素，则它代表的就是随机变量X_i与X_j之间的协方差。我们利用协方差主要是为了对变量间的二阶统计特性进行表示，在随机变量中，如果它们的不同变量之间的相关性比较小，那么最终所得到的协方差矩阵类似于一个对角矩阵。