11.2.3  CCA的基本性质

11.2.3 CCA的基本性质

设A=Σ₁^-11Σ₁₂Σ₂^-21Σ₂₁，B=Σ₂^-21Σ₂₁Σ₁^-11Σ₁₂，可以证明，A和B的特征向量和特征根具有如下性质：

1）A和B具有相同的非零特征根，且所有特征根非负。

2）A和B的特征根均在0～1之间。

3）设A和B的非零特征根为λ²₁≥λ²₂≥…≥λ²_r，r=rank（A）=rank（B），a（1），a（2），…，a（r）为A对应于λ²₁，λ²₂，…，λ²_r的特征向量，b（1），b（2），…，b（r）为B对应于λ²₁，λ²₂，…，λ²_r的特征向量，即典型变量。

典型变量具有如下性质：

（1）同一组的典型变量互不相关

设x、y的第i对典型变量为

u_i=a_i′x，v_i=b_i′y，i=1，2，…，m（11-23）

则有

V（u_i）=a_i′Σ₁₁a_i=1，V（v_i）=b′_iΣ₁₁b_i=1，i=1，2，…，m

ρ（u_i，u_j）=cov（u_i，u_j）=a_j′Σ₁₁a_j=0，1≤i≠j≤m

ρ（v_i，v_j）=cov（v_i，v_j）=b_i′Σ₂₂b_j=0，1≤i≠j≤m（11-24）

式（11-24）表明x组成的第一组典型变量u₁，u₂，…，u_m互不相关，且均有相同的方差1；由y组成的第二组典型变量v₁，v₂，…，v_m也互不相关，且也均有相同的方差1。

（2）不同组的典型变量之间的相关性

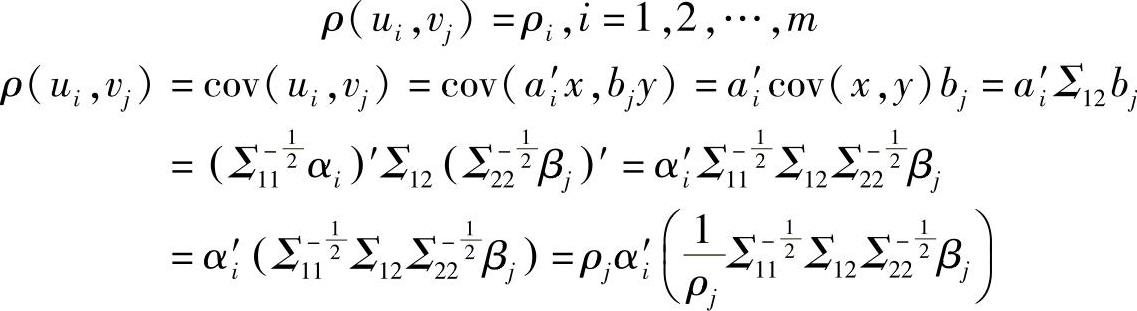
=ρ_jα_i′α_j=0 1≤i≠j≤m（11-25）

式（11-25）表明不同组的任意两个典型变量，当i=j时，相关系数为ρ_j，当i≠j时是彼此不相关的，记

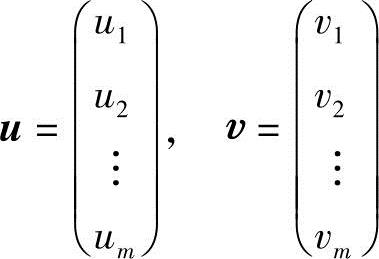
则上述性质可用矩阵表示为

V（u）=I_m，V（υ）=I_m，cov（u，υ）=cov（υ，u）=Λ

或如下所示：

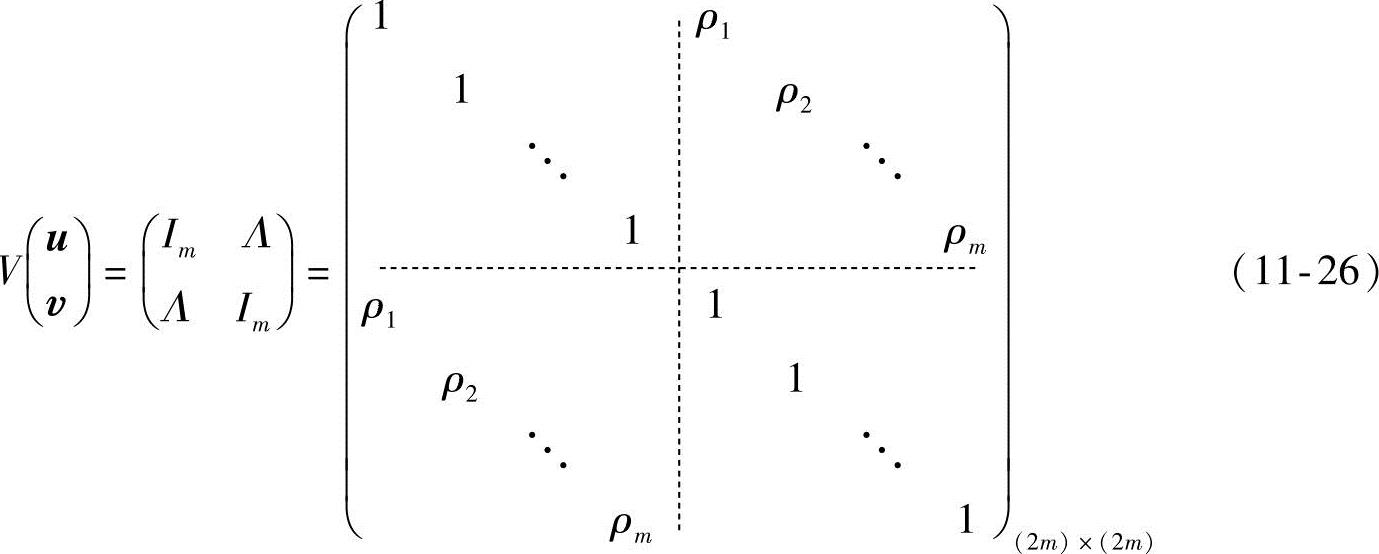
式中，

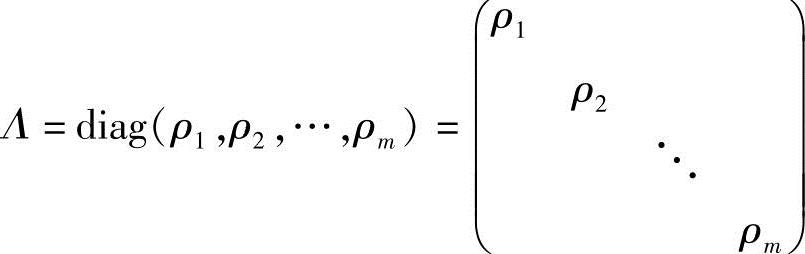
（3）原始变量与典型变量之间的相关系数