12.4.1 PSO优化问题分析
在对BP神经网络基函数参数优化之前,我们需要对下面几个问题进行分析和解决:
(1)确定对最优激活函数中参数的评价标准
在神经网络中对其内部进行数据训练主要是想要通过获得的相应网络参数可以使该神经网络中的平均误差2次方值的和达到最小,其计算公式为
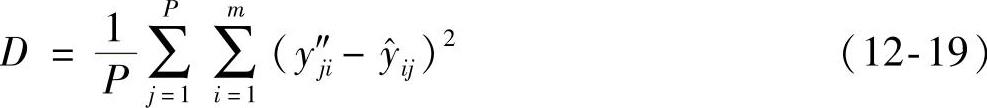
式中,用参数P来表示训练样本的总数;j=1,2,…,p;i=1,2,…,m,参数m代表的是输出层在神经网络中的节点数;yj″i表示节点输出值,即在总样本中第j个样本通过输出层中的第i个节点输出;y^ij表示节点预计输出值,即在总样本中第j个样本通过输出层中的第i个节点预计输出。
下面给出激活函数中参数评价的标准,即先激活函数中参数进行假设,即参数p=(c1,σ21,c2,σ22,…,ck,σ2k),在参数集中,利用ci=(ci1,ci2,…,cim),i=1,2,…,k,来表示节点中S型激活函数对应的中心,其中用k表示在隐层中的节点数,用m表示在输入层输入特征向量对应的维数,在上述参数中用σi来表示第i个节点的S型激活函数对应的宽度,然后对输入样本的特征向量进行训练,再对其进行归一化处理,其中0≤cij≤1,0≤σ2i≤1,j≤1,i=1,2,…,n。根据上述参数假设,通过假设的参数P来对BP神经网络进行有效可靠的组建,该网络平均误差和用D来表示,在激活函数参数的有效区域内如果对于其每一个相关的参数P而言,都会存在D(P∗)≤D(P),则此时P∗就是我们所要寻找的最优激活函数参数。
(2)粒子群中粒子初始化
假设在目标空间中粒子群的大小为N,那么可以通过这个空间来随机产生一个相应的粒子位置矩阵X和对应的速度矩阵V,它们两者可表示如下:
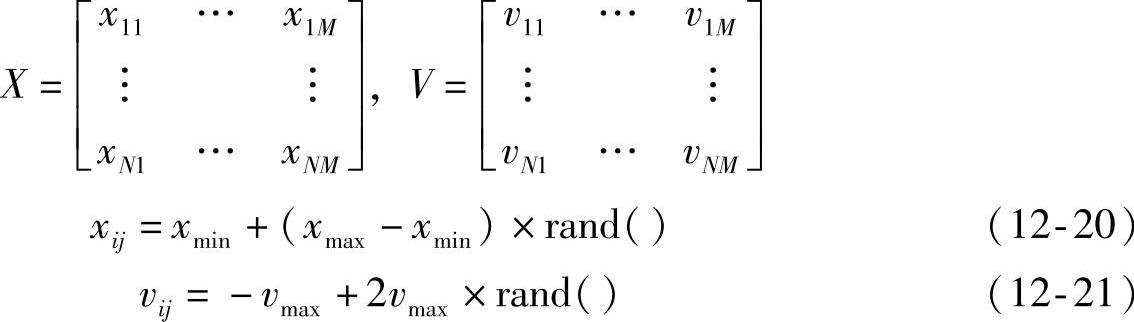
式中,M=k(n+1),其中用k来表示在神经网络隐层的节点数,输入层中相应输入特征向量的维数用n来表示;{xiji=1,2,…,N;j=1,2,…,M}指的是在空间粒子的相应位置向量所对应的分量,i表示粒子在空间的位置,j表示相应维数分量;(xi1,xi2,…,x1M)与BP神经网络核函数中的参数进行对应;xmax=1,xmin=0,0≤xij≤10;{viji=1,2,…,N;j=1,2,…,M}指的是在空间粒子的相应速度向量所对应的分量,i表示粒子在空间的速度,j表示相应维数分量。
(3)确定粒子的适应度函数
适应度函数决定了粒子在空间中相应位置的优劣度量,如果适应度函数的值越小,那么粒子的位置就越不好,具体定义为
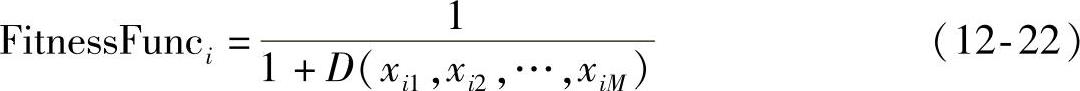
式(12-22)代表的是在粒子群中第i个粒子对应的适应度函数值,其中当核函数的参数是(xi1,xi2,…,xiM)的时候,此时神经网络的平均误差平方和就是D(xi1,xi2,…,xiM)。
