9.1.2 遗传算法流程
遗传算法从任一初始种群出发,通过随机选择、交叉和变异等操作,产生一群更适应环境的个体,使种群进化到搜索空间中更好的区域。经过一代代的不断繁衍进化,最后收敛到最适应环境的个体,即问题的最优解。遗传算法的一般流程如图9-1所示,由图可以看出遗传算法是一个典型的迭代寻优的过程,它的实现包括编码方法;初始化种群的产生;适应度函数以及由选择、交叉和变异组成的遗传算子;终止条件。
1.编码方法
由于遗传算法不能直接处理解空间的数据,因此必须通过编码将解空间的解数据转化为遗传算法所能处理的搜索空间的基因型串结构数据。常用的编码方法包括二进制编码、顺序编码、实数编码、整数编码等。编码方法对算法搜索能力、种群多样性等性能具有很大影响,需要根据所解决问题的实际需要,选择合适的编码方法。
2.初始群体的产生
遗传算法是一种基于种群寻优的方法,算法运行时是以一个种群在搜索空间进行搜索。我们必须为遗传算法操作准备一个由若干初始解组成的初始群体。初始种群是随机产生的,具体的产生方式依赖于编码方法。种群中个体的数量称为种群规模,记为N。种群规模影响着遗传优化的最终结果和遗传算法的执行效率。一般来说,遗传种群规模越大越好,但规模越大,其适应度评估次数增加越多,将导致运算时间的增大,通常设为100~1000。
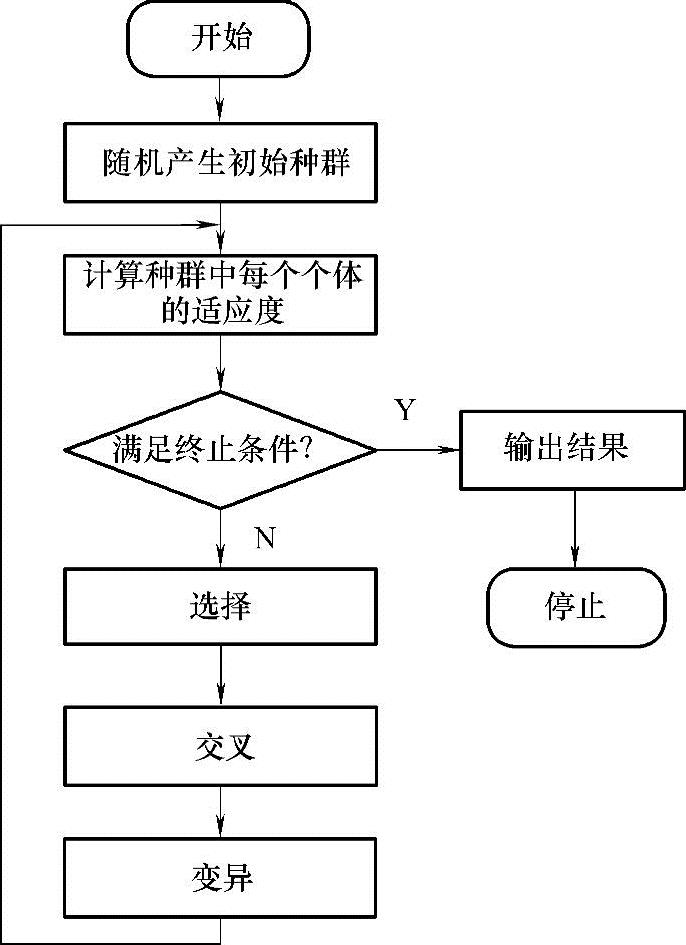
图9-1 遗传算法流程图
3.适应度函数
在遗传算法中使用适应度函数来表征种群中每个个体对其生存环境的适应能力,每个个体具有一个适应度,适应度是群体中个体生存机会的唯一确定性指标。因此适应度函数的选取直接影响遗传算法的收敛速度以及能否找到问题的最优解。适应度函数基本是依据优化的目标函数来确定,目标函数一般表示为f(x),适应度函数一般为F(x)。
对于目标函数最小值的优化问题,将其转化为求目标函数最大值的优化问题,即
F(x)=-minf(x)(9-1)
对于目标函数最大值的优化问题,可以直接设定目标函数为其适应度函数,即
F(x)=maxf(x)(9-2)
4.遗传算子
遗传算子模拟了每一代中创造后代的繁殖过程,是遗传算法的精髓,包括选择、交叉和变异。
选择是以一定的概率从当前种群中选择一部分个体的操作。在遗传算法中自然选择规律的体现就是以适应度大小决定的概率分布来进行选择。个体的适应度越大,该个体被遗传到下一代的概率越大;反之,个体的适应度越小,该个体被遗传到下一代的概率也就越小。选择操作的目的是保留优秀的基因,改善算法的全局收敛性以提高收敛速度。常用的选择策略是正比选择策略,即每个个体被选中进行遗传运算的概率为该个体的适应度与群体中所有个体适应度总和的比。对于个体i,设其适应度为Fi,种群规模为N,则该个体被选中的概率为

交叉是指同时对两个相互配对的染色体操作,组合两者的特性形成两个新的个体。通过交叉操作能从种群中寻找到父代双亲已有但未被合理利用的优良基因信息,扩大了遗传算法在解空间中的搜索范围,实现其全局搜索的目的。交叉率定义为各代中交叉产生的后代数与种群规模的比,记为Pc,一般取为0.4~0.99。
变异是在染色体上自发产生随机的变化,一种简单的变异方式是替换一个或者多个基因,从而形成一个新的个体。变异的目的:一是使算法具有局部搜索的能力,当遗传算法通过交叉算子的作用已接近最优领域时,利用变异算子的局部搜索性能可以加速向最优解收敛;二是维持群体多样性,防止出现未成熟的收敛现象。变异率定义为种群中变异基因数在总基因数中的百分比,记为Pm,一般取为0.0001~0.1。
5.终止条件
遗传算法的终止条件一般采用设定最大进化代数的方法,最大进化代数常表示为T,一般取为100~500。
