13.2.2 结构风险最小化
经验风险最小化原则是经过实践验证的有效的学习停止规则,并被应用到了众多的识别算法中,但是它所应用的情况也是具有局限性的。比如观测样本必须最够多,在大量的数据中寻找某个规律并总结经验,使得在以后的预测过程中犯错的可能性达到最小,也就是先验知识和经验足够丰富才行。对于小样本数据问题,往往不能通过现有的数据从中得到较为有效的先验知识,从而造成置信范围过大。神经网络等方法就是采用经验风险最小的原则,然而神经网络的网络结构是具有不确定性的,针对不同问题采用的网络结构不同,最后得出的效果差异也较大。因此在网络的设计过程中对操作人员的技巧具有很强的依赖性。
针对经验风险最小化的问题,统计学习理论提出了一种新的学习停止规则,被称为结构风险最小化准则。结构风险最小化准则的基本思想可以通过图13-5进行说明。通过图13-5我们可以看出,所谓结构风险最小是指首先通过函数集中不同子集VC维(Vapnik-Chervonenkis dimension)的大小对这些子集进行排序,之后在子集的内部搜寻最小经验风险,然后在子集之间添加对置信范围的考虑,最后取一个折中值。
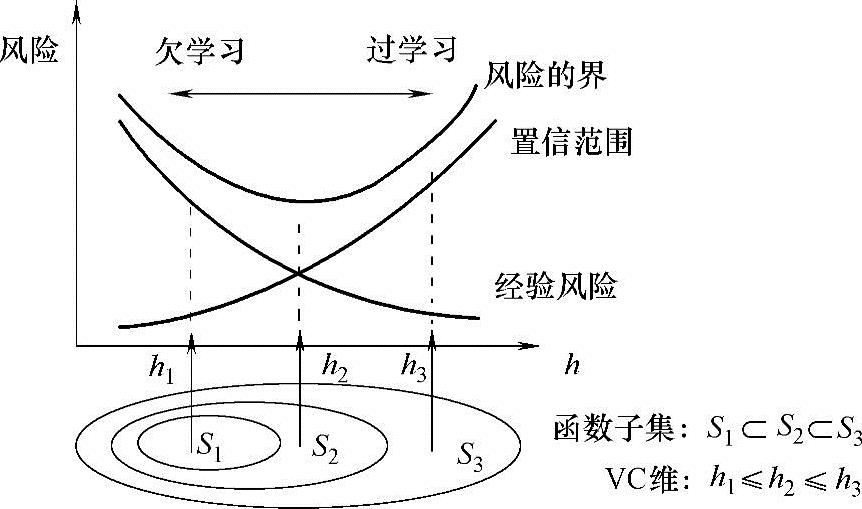
图13-5 结构风险最小化准则
通过上述描述可知,经验风险和置信范围分别取决于不同的对象,置信范围是取决于函数集的,而经验风险往往是由某个具体的函数来决定的。统计学习理论对结构风险最小化原则进行了详细的论证。首先对结构风险最小化准则下实际风险能够收敛的性质进行了证明,还对模型的选择给出了严密的论证过程,不仅如此,它还对函数子集结构的合理性提出了相应的标准。
基于对函数集重要性的考虑,统计学习理论对其各种类型进行了细致的研究。希望能够通过对它们详细的研究来更好地了解泛化界限,也可以简单地理解为是寻找它与经验风险和实际风险之间的内在关联。
不失一般性,我们这里对两分类问题进行讨论,可以得到如下的结论:经验风险Remp(w)和实际风险R(w)之间有如下关系:
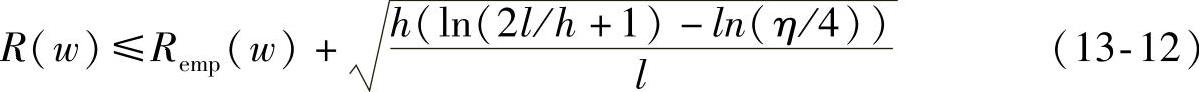
式中,h为VC维,l是样本个数的具体数值,η取值范围为0≤η≤1。根据公式可以看出,小于等于号右边由两项构成,也就是实际风险R(w)可以分为两部分:一部分是我们所熟知的经验风险Remp(w),另一部分我们可以称其为置信界限。并且公式中的置信界限是由分类器的VC维h和训练样本数l共同确定的,它是对复杂结构所带来的风险的一个度量。所以式(13-12)也可以简单地表示为
R(w)≤Remp(w)+Φ(h/l)(13-13)
由式(13-13)右侧第二项可以看出,Φ(h/l)与h成正比。过学习的现象就是由于在训练样本有限的情况下,学习机器的复杂性过高、VC维较大,此时正比于VC维的置信界限自然也就较大。通过式(13-13),置信界限大意味着真实风险与经验风险之间的差别大,从而出现了过学习的现象。所以,我们可以通过调整分类器的泛化能力来解决这个问题,这样就可以构造适于小样本的分类器。对于有界非负函数,0≤L(z,w)≤B,w∈Λ,以大于或等于1-η的概率满足下面的公式:
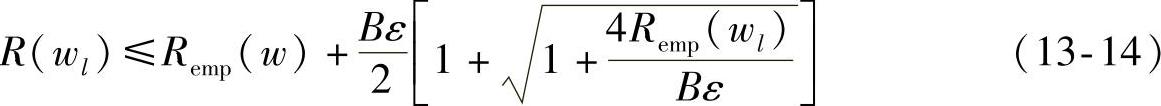
同样的考虑无界限集合,我们可以得到分类器的泛化能力:

式中,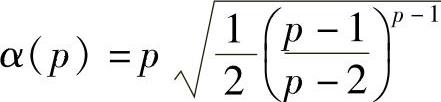 ,
,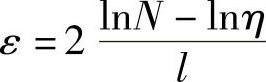
通过以上描述可知,经验风险越小,风险的上界也在减少,最小化经验风险或者最小化式(13-14)小于等于号右边的第二项,都可以调控最小化过程。显然,后者适合小样本情况。
