6.2.3 特征提取与融合
特征提取是目标分类识别的前提,特征提取的好坏,直接影响到识别结果。选取时应遵循的原则如下:
1)在保证目标正确识别的前提下,选取尽可能少的特征参数。
2)尽量选取计算量小,准确率高的特征参数。
3)选取的特征量鲁棒性要高,即具有平移、比例和旋转等不变性。
4)特征量之间的相关性要尽量小。
在特征提取的过程中,提取的特征量是具有独立性、可靠性、数据量少和可区别性的特点,这样才能增强目标识别系统的可靠性和准确性。
根据以上原则,可以提取红外图像的形状特征和可见光图像的边缘特征。
特征融合,即把从不同传感器提取的特征,通过某种算法,重新组合成一个新的特征向量,新的特征向量用作后续目标分类和识别的判断依据。
特征级融合算法可分为两大类:特征选择和特征组合。将所有的特征量放在一起,用某种方法产生一个新的特征向量,新向量中的元素都是从原向量选择得到的,称为特征选择,例如,遗传算法。将所有向量直接组合成新向量,称为特征组合,例如,串行和并行融合策略。
(1)串行融合策略
设A和B是在样本模式空间Ω的两个特征空间。对于任意样本Γ∈Ω,相应的特征表示向量为A∈α和B∈β。串行融合策略将这两个特征表示向量串成了一个大向量γ,公式如下:

由式(6-75)可知,若α是n维的,β是m维的,那么合成的向量γ为(m+n)维的。因此,所有由串行融合而成的向量,是一个(m+n)维的新特征空间,后续的分类识别就是在这个新特征空间中进行的。
(2)并行融合策略
设A和B是在样本模式空间Ω的两个特征空间。对于任意样本Γ∈Ω,相应的特征表示向量为A∈α和B∈β。并行融合策略将这两个特征表示向量合成了一个复向量γ,公式如下:
γ=α+iβ(6-76)式中,i为虚数单位。需要注意,如果α和β维数不一致,那么需要对低维的向量补0。例如,α=(α1,α2,α3)T,β=(β1,β2)T,则首先将β变为β=(β1,β2,0)T,然后合成向量γ=(α1+iβ1,α2+iβ2,α3+i0)。
在Ω上定义一个并行融合的特征空间C={α+iβα∈A,β∈B}。显然,这是一个n维的复向量空间,其中n=max(dimA,dimB)。在这个空间里,内积可定义为
(X,Y)=XHY(6-77)式中,X,Y∈C,H表示共轭转置。
定义了以上内积的复向量空间,被称为酉空间。在酉空间可引入以下范数:
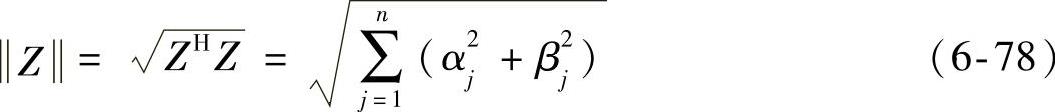
式中,Z=(α1+iβ1,α2+iβ2,…,αn+iβn)T。相应地,复向量Z1和Z2之间的距离可定义为
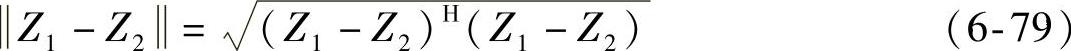
并行融合策略与串行策略相比,降低了融合后向量的维数。更重要的是,它引入了酉空间的概念,从而把两个实向量空间的融合问题转化为一个复向量空间的数学问题。
(3)遗传算法
遗传算法模仿了生物的进化过程。该算法将问题的可能解编成0、1代码串,称为染色体。若给定一组初始的染色体,遗传算法就会利用遗传算子对其进行操作,产生新一代染色体。新一代染色体可能包含了较前代更好的解。每一条染色体都要通过适应度函数去评价其适宜程度,遗传算法的目标是找到最适宜的染色体。
遗传算法主要由四部分组成:遗传算子、编码机制、控制参数、适应度函数。
编码机制是遗传算法的基础。遗传算法不是对研究对象直接进行讨论,而是通过某种编码机制把对象统一赋予由特定符号按一定顺序排成的串。在常用的遗传算法中,染色体由0与1组成,码为二进制串。对遗传算法的码可以有十分广泛的理解。在优化问题中,一条染色体对应于一个可能解。
在遗传算法中,用适应度函数来描述染色体的适宜程度,即根据其适应度来评估染色体优劣。
遗传算法最重要的算子有:选择、交叉、变异。选择的作用是根据染色体的优劣程度决定它在下一代是被淘汰还是被复制。交叉算子是让不同的染色体可以进行信息交换。变异算子就是改变染色体的某个位置上的值。
在实际操作过程中,为提高选优的效果,需先适当地确定某些参数的取值。例如,每一代的群体大小、交叉率和变异率,此外还有遗传的代数,或其他可供确定中止繁殖的指标。
例如,假设α和β分别表示某一目标的两类不同特征。通过遗传算法,可以得到融合的特征向量γ,表达式如下:
γ=f(α,β,x)(6-80)式中,x为最优染色体。x的每一位与特定位置的特征成分相关,该位的取值决定了这个位置的特征成分是从α选择(值为1)还是从β选择(值为0)。
