13.2.1 经验风险
机器是不具有思考能力的,因此机器的学习过程是需要人为地制定学习规则的,也就是对学习内容、学习方式以及学习的停止准则进行规定。其中学习停止准则最为重要,因为如果机器在还没有完全获得必要的知识之前就停止学习,那么它的识别能力也就可想而知了;相反,如果出现了过学习现象,那么机器的泛化能力也会下降,这也是我们不希望看到的。所以对学习准则的制定需要进行多方面的考虑,而经验风险最小化的原则是较为实用的停止准则之一,下面我们对这一停止原则进行解释。
假设有l个观测样本(x1,y1),(x2,y2),…,(xl,yl),它们之间是相互独立的关系,但是遵循一样的分布规律,y和x之间的关系是满足一个未知的联合概率密度函数F(x,y)。预测函数集{f(x,w)}中存在可以使得期望风险R(w)最小的一个预测函数f(x,w0),称之为最优函数。对期望风险R(w)的定义为
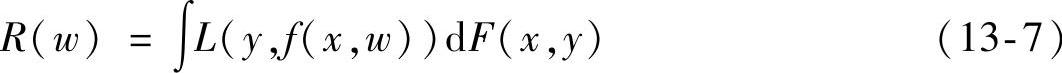
式中,我们将{f(x,w)}称之为预测函数集合,w为函数的广义定义参数。{f(x,w)}可以表示任何函数集。L(y,f(x,w))为由于用f(x,w)对y进行预测而造成的损失,针对学习的情况不同,损失函数的形式也不相同。
机器学习最常应用于以下三类:分类问题、回归估计问题和概率密度估计问题。对于分类问题,输出y的形式为y={0,1}或y={1,1},该类问题的损失函数可以定义为以下形式:
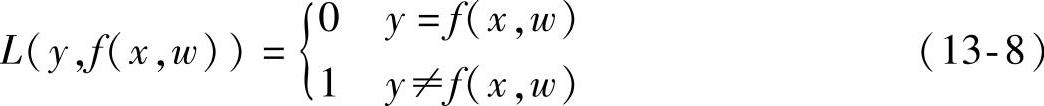
针对目标识别问题,我们期望通过对现有样本数据学习的过程,找到一个使得错分概率最小的分类函数f(x,w0),并且学习过程是在F(x,y)未知的情形下进行的。如果分类器的输出与期望值不符,那么我们称该次分类为错分。
在函数回归估计问题中,y的值是一个连续变量,损失函数定义为
L(y,f(x,w))=(y-f(x,w))2(13-9)
回归函数就是在损失函数下能够使得风险泛函式(13-7)取值最小的函数。
概率密度估计问题不同于模式识别,模式识别具有期望输出,而概率密度估计没有这样一个期望值来做对比,它的目的是通过对现有样本的学习来大概估计x的概率密度,其中被估计的密度函数为p(x,w)。此类问题的损失函数也不同于模式识别,具体形式定义如下:
L(y,f(x,w))=-logp(x,w)(13-10)
虽然各问题的应用方向不一样,但通过对以上问题的描述可以看出,它们都是以期望风险最小化为学习目的的。但是由于受到各种条件限制,比如样本数量较少、概率密度F(x,y)未知,所以式(13-7)表示的期望风险无法估计。针对此类问题,传统的学习方法是通过计算样本的误差来定义经验风险的:
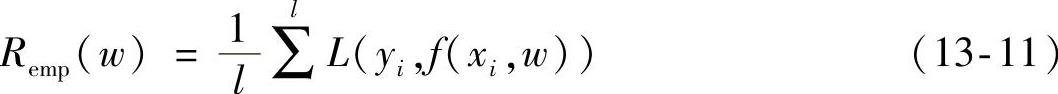
我们将这种利用样本误差来定义经验风险的方法称之为经验风险最小化(Empirical Risk Minimization,ERM)原则。
统计学习的任务就是要找到合适的方法最小化Remp(w)来替代式(13-7)。针对不同的问题,具有不同的损失函数,其对应的经验风险的含义就会不同。比如,模式识别问题中的经验风险是错分率,而回归问题中的经验风险却是平方训练误差。许多经典算法都采用了基于经验风险最小化的原则,比如最小二乘法、最大似然估计法这些算法都是采用了经验风险最小化的原则,另外还有神经网络学习方法也是采用了同样的学习原则。
