3.3.1  低通滤波

低通滤波的原理是去除傅里叶变换中所有高频成分，即通低频、阻高频，保留有用的低频信息。其原理框图如图3-5所示。图中，f（x，y）为原始图像，F（u，v）为经过傅里叶变换的图像，G（u，v）为低通滤波后的图像，且滤波后的图像G（u，v）要经过低通滤波的传递函数H（u，v）获得，最后经过傅里叶逆变换而获得去噪后的图像g（u，v）。滤波后的图像G（u，v）的表达式如下：

图3-5 低通滤波原理框图

G（u，v）=F（u，v）H（u，v）（3-14）

低通滤波包括：理想低通滤波、指数低通滤波和巴特沃兹低通滤波。其中理想低通滤波的描述见式（3-15），指数低通滤波的描述见式（3-16），巴特沃兹低通滤波的描述见式（3-17）。其中，D₀代表被指定距离且为非负数值，D（u，v）代表点（u，v）与频率矩形原点的距离。

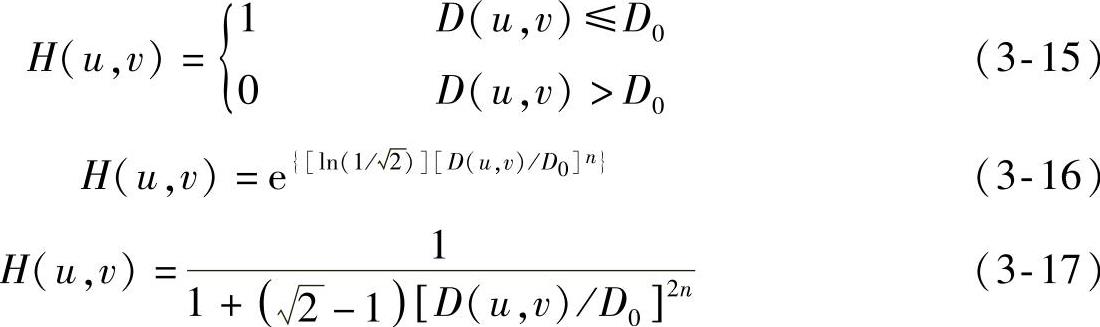
由于图像中高频段多集中噪声频谱，而低、中频段常集中图像的有用信息，所以这几种低通滤波可以去掉突变的高频成分与尖峰噪声。低通滤波滤掉了跳变性的高频分量，这就意味着滤除了图像边缘的跳变信息，从而造成了图像边缘模糊现象，因此，这种滤波算法是以牺牲图像的清晰度为代价而换取的。