7.2.2  协方差矩阵距离的度量

7.2.2 协方差矩阵距离的度量

在矩阵理论发展的历史中，如何比较两个矩阵是一个非常经典的问题，在我们传统的欧式空间运算中，因为协方差在其运算中封闭性比较差，所以不能在传统的欧式空间中解决协方差矩阵之间的度量问题，所以通过查阅了一些文献后，这里主要借鉴一种解决协方差直接距离度量的方法，如下：

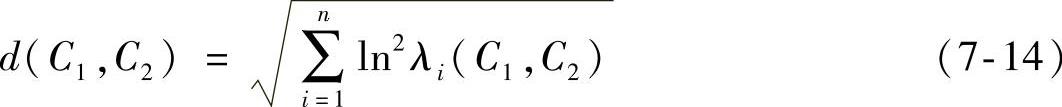
在式（7-14）中，{λ_i（C₁，C₂）}_i=1，2，…，n是一个特征方程，它是由C₁和C₂特征值组成的，其中这些特征都是正定矩阵，它具有下面几个特性：

1）正定性d（C₁，C₂）≥0，其中等号当且仅当C₁=C₂时才会成立。

2）对称性d（C₁，C₂）=d（C₂，C₁）。

3）三角不等式d（C₁，C₂）+d（C₁，C₃）≥d（C₂，C₃）。

根据式（7-14），这里存在式（7-15）：

det（λC₁-C₂）=0（7-15）通过式（7-15）再对其进行有效的简化推导可得下式：

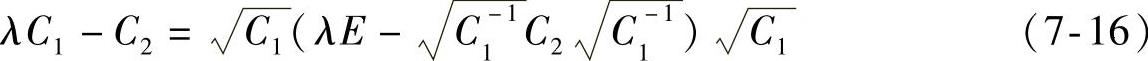
因为C₁和C₂都属于正定矩阵，所以在式（7-16）中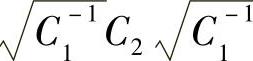的特征值都是正定数。所以可以通过利用雅克比过关法来对式（7-16）解得特征值，其中最关键的是需要将λ₁（C₁，C₂），…，λ_d（C₁，C₂）通过转换为正定实矩阵来进行计算，这样最终才能正确且更少计算量地求得特征值。

图7-2是协方差矩阵的一个构造流程图。

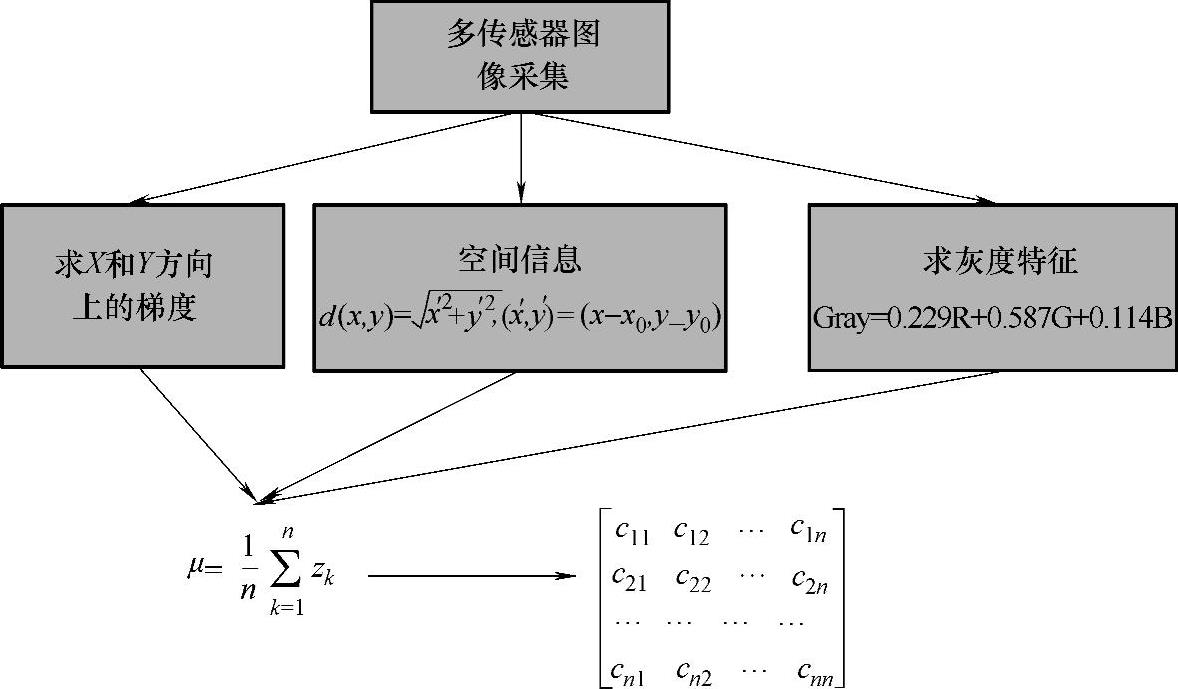
图7-2 协方差矩阵的构造流程