12.3.2  过圆外一点的直线与圆相切的切点坐标计算

12.3.2 过圆外一点的直线与圆相切的切点坐标计算

由圆外一点向圆作切线，切线与圆相切的切点是，如图12-5所示。由于切线过P_o点，故P_o的坐标满足切线方程，即；又P_o在圆上，故P_o的坐标满足圆的方程，即。由此可知，求切点坐标只要联立求解上面两个方程组即可。

计算切点坐标的公式为

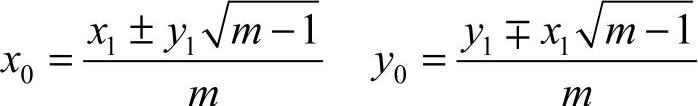
其中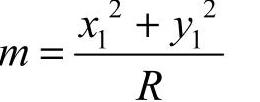

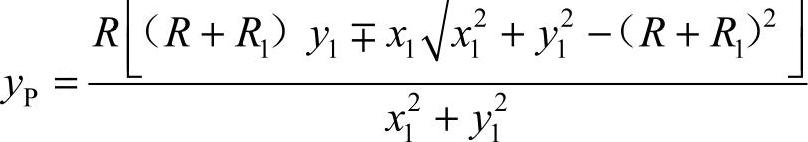
如果是图12-6a所示的公切线Ⅰ的情况，即P点对应于α+β，则x_P取“−”号；如果是图12-6b所示的公切线Ⅱ的情况，即P点对应于α−β，则x_P取“+”号。而y_P的符号与x_P的符号取法相反。

接着求出切点Q的坐标。由于P点在XOY坐标系的坐标P（x_P，y_P）与Q点在坐标系的坐标有比例关系，因此切点Q在坐标系的坐标为

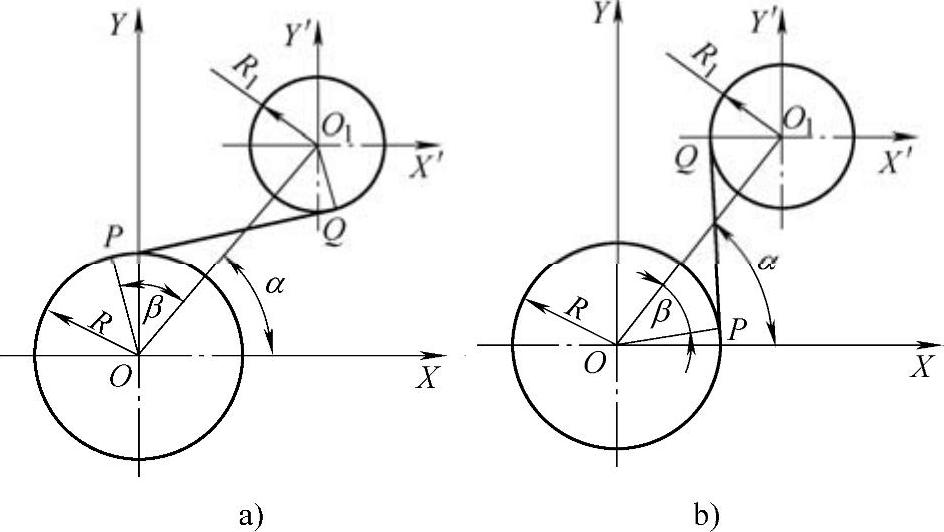
图12-6 两圆内公切线切点坐标的计算

a）公切线Ⅰ b）公切线Ⅱ