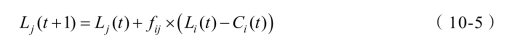10.2.2　负载分配模型

10.2.2　负载分配模型

根据节点容量与负荷的差异，我们引入失效概率 pi，定义节点的三种状态，如式（10-2）所示：

式中 rand ── 0～1 的随机数；

pi=，为节点i 的失效概率。

负载疏散时，考虑到对旅客影响最大的两种因素连边冗余能力与相连节点的距离，我们构建基于这两种因素的效应指标 fij，具体如式（10-3）所示：

式中 φ ── 节点i 的相连节点集合；

Cij── 边ij 的容量；

Lij── 边ij 的负载；

dij── 边ij 之间的距离。

观察式（10-3）易知，连边冗余能力越大，相连节点距离越小，对负载的吸引力越强。

若节点i 在t 时刻失效，则下一时刻，其向相连节点j 的负载分配公式如式（10-4）所示：

若节点i 在t 时刻暂停，则下一时刻，只向相连节点疏散过量负载，使其恢复正常，其向相连节点j 的负载分配公式如式（10-5）所示：