10.4.1 标准PSO 算法
粒子群算法是一种模拟鸟类觅食行为的全局搜索优化算法，它将鸟类在觅食过程中的位置近似为目标问题的一个潜在解，通过个体之间的信息共享机制，引导种群向最优解方向靠拢，以此实现对目标问题的优化[30]。在标准粒子群算法中，每个粒子都存在位置和速度两个指标，粒子的位置即是解空间待解决优化问题的一个解，而粒子的速度则引导粒子不断改变自身位置。此外，每个粒子都存在一个目标函数，称为粒子的适应度，粒子依据自身适应度值与种群最优适应度值的比较，不断调整自己的位置，力图使自身更靠近最优解。
假设由N 个粒子组成的种群在一个D 维解空间，第i 个粒子的位置xi=( xi1, xi2, …, xid)， 速度vi=( vi1, vi2, …, vid)， 粒子个体最优解位置pi=( pi1, pi2,… , pid)，种群全局最优解位置gbest=( g1, g2,… , gd)，则第i 个粒子的第j 个维度在第 t+ 1次迭代过程中的速度更新公式如式（10-7）所示，位置更新公式如式（10-8）所示。
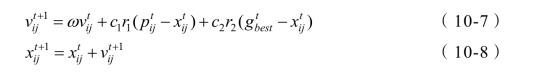
式中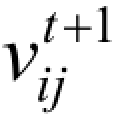 
── 第i 个粒子的第j 个维度在第 t+ 1次迭代后的速度；
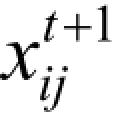── 第i 个粒子的第j 个维度在第 t+ 1次迭代后的位置；
ω ── 惯性权重，表征粒子保持原有搜索速度的能力，ω 值越大，粒子的全局搜索能力越强，但搜索效率较低，ω 值越小，粒子局部搜索能力越强，解的精度越高，但容易陷入局部最优；
c1── 学习因子，表征粒子对自身的学习能力；
c2── 学习因子，表征粒子对种群的学习能力；
r1、 r2── 介于[0,1]之间的随机数；
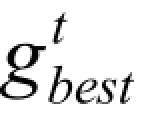── 种群第t 次迭代时全局最优解在对j 个维度的位置。
为降低粒子在搜索过程中离开解空间的可能性，通常规定粒子存在一个最大速度 vmax和最小速度 vmin，即有vij∈[vmin,vmax]。