10.5.2 基于PSO&MPSO 算法的城市群轨道-道路耦合交通网络...
本部分以呼包鄂榆城市群轨道-道路耦合交通网络为例，分别用标准粒子群与优化后的粒子群算法对网络节点容量进行优化，对于节点i，假定优化前其容量为 Ci，则规定优化过程中节点i 容量为ξ Ci，其中ξ ∈[0.8,1.2]。运用粒子群算法对网络节点容量进行优化，设定网络节点负载因子α = β=0.8，连边负载因子μ =0.8，粒子群规模N = 30，最大迭代次数T =300，学习因子 c1=0.5、 c2=0.5，粒子最大速度 vmax= 5，最小速度 vmin=-5 ，标准粒子群惯性权重ω =0.8，改进粒子群惯性权重最大值 ωmax=1.2、最小值 ωmin=0.8，临界平均适应度方差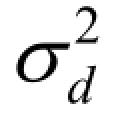
=0.1，变异概率x=0.5。改进后的粒子群算法记为MPSO。
进行随机攻击时，对于网络当前的所有有效节点随机攻击网络 500次，记录各次攻击的抗毁度值，选择抗毁度中值所对应的节点作为该次攻击的目标节点。如此循环，将连续攻击λ 次后的网络抗毁度作为粒子当前的适应度值。为了全面考察优化算法的特性，本章分别取λ = 10、λ =100，运用PSO、MPSO 算法对网络节点容量进行优化，并对优化后的网络进行随机攻击下的抗毁性仿真，以此检验算法的优化效果。
（1）λ = 10时基于PSO&MPSO 算法的城市群轨道-道路耦合交通网络节点容量优化仿真分析。
将连续随机攻击 10 次后的网络加权最大连通子图相对规模作为粒子的适应度值，MPSO 算法适应度理论最优值下限fd=0.9976，算法收敛过程如图10-2（a）所示，优化结果如图10-2（b）所示。对未优化、PSO 算法优化、MPSO 算法优化三种情况的网络进行随机攻击策略下的抗毁性仿真，采用既定的随机攻击策略，连续攻击节点至网络完全崩溃，网络抗毁度变化如图10-2（c）所示。
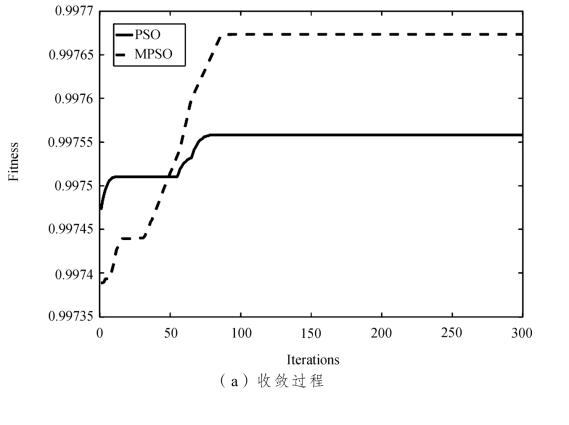
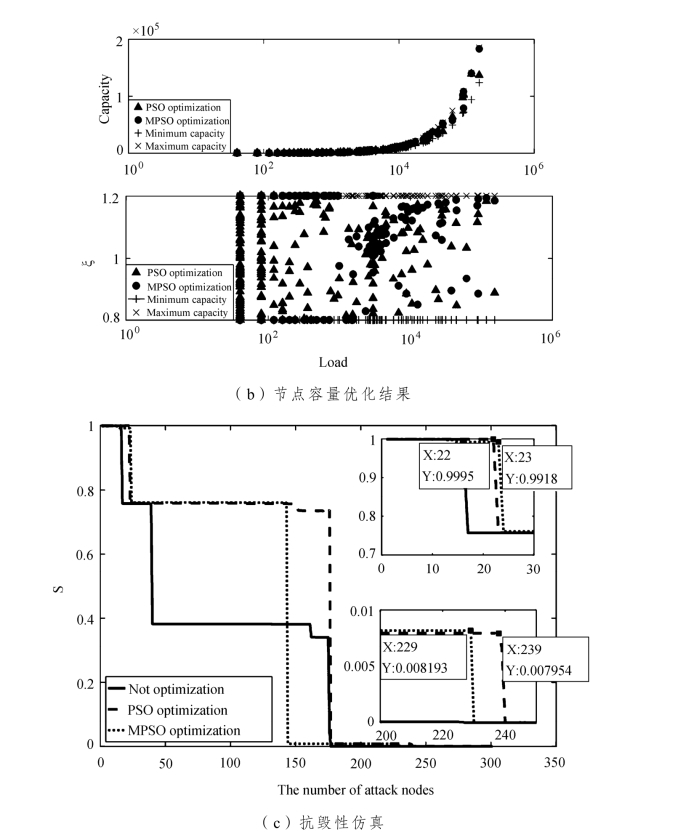
图10-2 λ= 10时PSO&&MPSO 算法容量优化结果及抗毁性仿真
如图10-2（a）所示，随着迭代次数的增加，种群最优适应度不断增大，标准粒子群算法在70 次迭代之后收敛于最优解0.997552，改进粒子群算法在80 次迭代后收敛于最优解0.997655，相比而言，改进后的粒子群算法能够更加有效地完成对最优解的寻找，收敛精度提高了0.000103。此外，观察图10-2（a），可以发现迭代初期改进粒子群算法对最优解的搜索效率更高，种群最优适应度值快速增加。
观察图10-2（b），我们发现由标准PSO 算法优化之后的网络，不同负载所对应的节点容量在给定区间内均匀分布，没有表现出较大的区分。而由改进PSO 算法优化之后的网络，对于负载较小的节点，容量往往趋于极值，即到达给定区间的边界，容量系数ξ 集中于0.8 与1.2 这两个值；当负载增大到一定值，其对应的容量系数则集中于[1,1.2]这个区间内。
如图10-2（c）所示，随着攻击节点数的增多，网络抗毁度不断下降，优化后的网络抗毁性表现相较于优化前改善显著。采用同种攻击策略，未优化网络在攻击第17 个节点时出现跳跃性下降，标准PSO 优化后的网络在攻击第23 个节点时出现跳跃性下降，改进PSO 优化后的网络在攻击第24 个节点时出现跳跃性下降，这表明三种网络对随机攻击的承受能力逐渐增强，采用改进的粒子群算法对网络进行优化，网络抗毁性的提升明显好于标准粒子群的优化效果。
同时，我们发现当攻击节点数超过100 之后，优化后的网络抗毁性表现仍然强于未优化网络，但由标准PSO 优化得到的网络抗毁性表现要优于由改进PSO 优化得到的网络，具体表现有：
① 由改进PSO 优化后的网络在攻击第144 个节点时出现第二次跳跃性下降，而标准PSO 优化后的网络第二次跳跃性下降则发生在攻击第178 个节点时；
② 标准PSO 算法优化后的网络在攻击第239 个节点后全局崩溃，改进PSO 算法优化后的网络在攻击第230 个节点后便全局崩溃。
综上，优化后的网络抗毁性表现相较于优化前有了明显的改善，同时，相较于由标准PSO 优化得到的网络，由改进PSO 优化得到的网络在攻击前期表现出更好的抗毁性，而在后期的抗毁性表现则不如由标准PSO 算法优化得到的网络。结合图10-2（b），我们认为这是由于改进PSO算法使得优化后网络中的大容量节点容量进一步得到增强，由此加强了网络初期对于级联失效的承受能力，而当攻击持续进行时，一旦关键节点受到破坏，网络的崩溃速度便突然加快，符合无标度网络的特征。
（2）λ =100时基于PSO&MPSO 算法的城市群轨道-道路耦合交通网络节点容量优化仿真分析。
将连续随机攻击100 次后的网络加权最大连通子图相对规模作为粒子的适应度值，MPSO 算法适应度理论最优值下限fd=0.412，算法收敛过程如图10-3（a）所示，优化结果如图10-3（b）所示。对未优化、PSO算法优化、MPSO 算法优化三种情况的网络进行随机攻击策略下的抗毁性仿真，采用既定的随机攻击策略，连续攻击节点至网络完全崩溃，网络抗毁度变化如图10-3（c）所示。
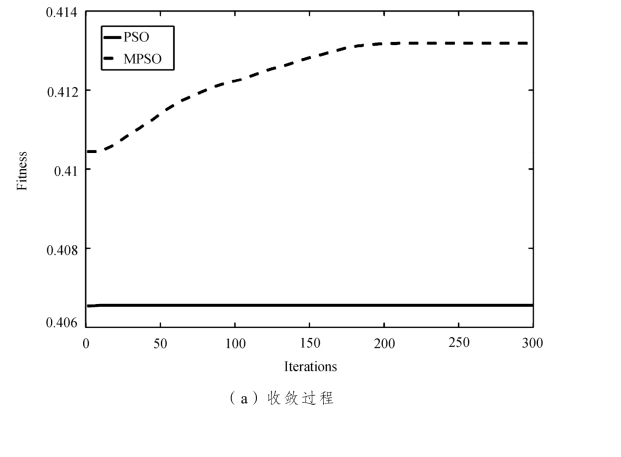
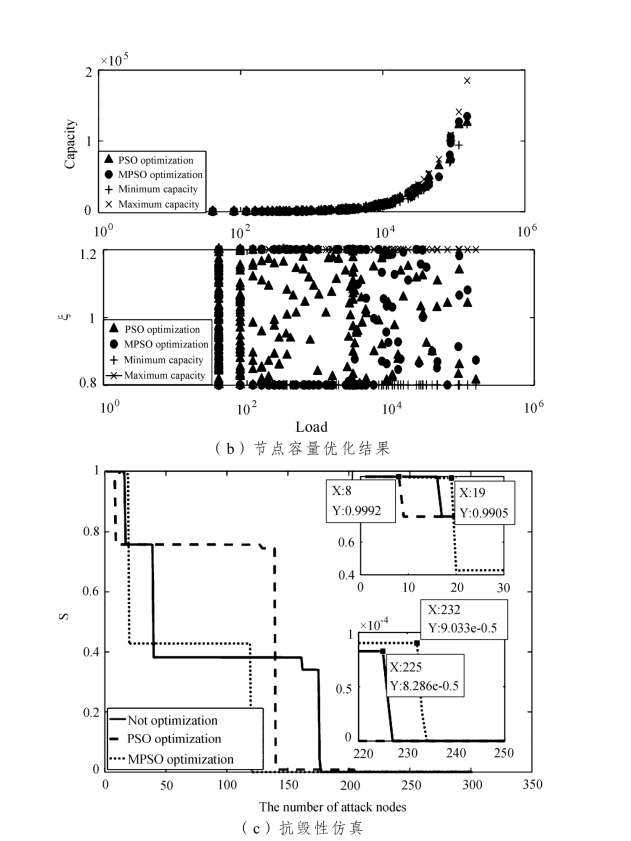
图10-3 λ=100时PSO&&MPSO 算法容量优化结果及抗毁性仿真
如图10-3（a）所示，随着迭代次数的增加，标准PSO 算法在9 次迭代后迅速收敛于0.4066，种群最优适应度值几乎不发生改变；改进PSO算法在189 次迭代后收敛于0.4132，种群最优适应度值不断增大。改进后的PSO 算法的搜索性能明显要优于标准PSO 算法。
观察图10-2（b），可以发现改进PSO 算法优化后的网络在负载较小时的容量系数ξ 集中在0.8 与1.2 上，当负载超过一定值后，其对应的容量系数则均匀分布在区间[0.8,1.2]上。结合4.2.1 小节的分析，我们认为这样的分布减弱了城市群交通网络的无标度特征，使得网络在攻击后期依然能够保持较强的抗毁性能。
如图10-3（c）所示，随着攻击节点数的增多，网络抗毁度逐渐下降，容易发现由改进 PSO 算法优化的网络抗毁性表现优于未优化以及由标准PSO 算法优化的网络，攻击第20 个节点时出现第一次跳跃性下降，攻击第233 个节点时网络完全崩溃。相较而言，由标准PSO 算法优化的网络抗毁性表现最差，攻击第9 个节点时便出现了跳跃性下降，攻击第208 个节点时网络完全崩溃。因此，改进PSO 算法达到了优化的效果，提升了网络面对随机攻击的健壮性，而标准PSO 算法由于种群最优解的早熟收敛，并没有达到网络抗毁性优化的目的。