10.4.2 改进PSO 算法
（1）基于logistic 函数的混沌映射。
在标准粒子群算法中，影响算法收敛性的一个重要因素就是粒子群的初始解，即初始种群的选取。初始迭代时，由于难以知道最优解在解空间的哪个区域，因此在标准粒子群算法中，只能用完全随机的方法来确定初始种群的位置，假如初始种群中的粒子均大致分布在全局最优解的附近，那么种群在较少次迭代之后便可收敛于全局最优解；反之，若初始种群的位置选取不当，恰好分布在局部最优解附近，那么种群将在数次迭代之后迅速收敛于局部最优解，由此将对粒子群算法的寻优能力造成极大影响。
综上，鉴于初始解的选取对 PSO 算法寻优能力的影响，本章使用logistic 函数对初始解进行混沌映射，使得初始种群均匀分布在解空间内，增加粒子靠近全局最优解的概率。首先，将第一个粒子的位置 x1′j在0 至1 范围作随机化处理，之后，粒子的迭代公式如式（10-9）所示：
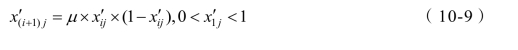
式中 μ ── 控制参数，当μ = 4，且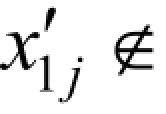 
{0,0.25,0.5,0.75}时，logistic处于完全混沌，此时粒子在解空间内均匀分布。
最后，将粒子的位置映射至原解的空间，具体如式（10-10）所示：
式中 xijmin── 第i 个粒子在第j 个维度的解的下限；
xijmax── 第i 个粒子在第j 个维度的解的上限。
至此，可以得到种群中所有粒子的初始位置。
（2）自适应惯性权重的改进。
惯性权重表征粒子保持原有搜索速度的能力，其值直接影响粒子的全局搜索能力与局部寻优能力，一般认为，惯性权重越大，粒子的全局搜索能力越强，但搜索效率较低，惯性权重越小，粒子的局部搜索能力越强，但容易陷入局部最优，因此，能否合理设置惯性权重值将对种群的寻优能力造成极大影响。
基于此，为使PSO 算法具有更强的寻优能力，我们使惯性权重在初期保持较大的值，随着迭代的进行，逐步减小惯性权重的值，如此，使种群在初期具有更强的全局搜索能力，而在后期具有更强的局部搜索能力，增大种群的收敛速度。由此，建立线性递减的惯性权重表达式，具体如式（10-11）所示：
式中 ω (t ) ── 第t 次迭代的惯性权重；
ωmax── 惯性权重最大值；
ωmin── 惯性权重最小值；
T ── 最大迭代次数。
（3）基于群体相似度的自适应变异算法。
随着迭代次数的持续增加，PSO 算法种群中的每个粒子在最优解的引导下，必然导致粒子之间的适应度变得越来越相似，这使得标准粒子群算法很难对当前搜索到的解进行进一步优化。基于此，本章从粒子的适应度相似度出发，引入变异系数，使相似粒子在一定概率下进行变异，从而增加种群跳出局部最优解的可能，保证算法的全局搜索能力。
部分文献从理论上证明粒子群算法早熟收敛时将聚集于某几个特定位置，并定义了描述粒子群聚集程度的指标群体适应度方差，本章对该指标进行改进，引入指标平均适应度方差σ 2，计算公式如式（10-12）所示：
式中 N ── 粒子个数；
fi── 第i 个粒子的适应度；
favg=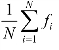
── 种群当前的平均适应度。
平均适应度方差σ 2反映了种群中粒子的聚集程度，σ 2越小，表明种群中粒子的聚集程度越高，σ 2= 0时，种群中所有粒子收敛于一至多个特定位置，并拥有完全相同的适应度。
针对粒子群算法的“早熟收敛”，本章在种群收敛至一定程度时对粒子作变异处理，使其尽可能广地在全局范围内进行最优解的搜索，引入变异系数 pm，计算公式如式（10-13）所示：
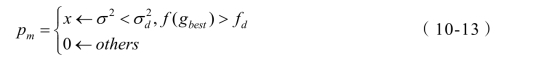
式中 x ── 粒子的变异概率，x∈(0,1]，其值可人为设定；
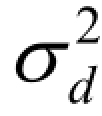── 临界平均适应度方差；
fd── 理论最优值的下限。
对于满足变异条件的种群，本章采用基于高斯分布的局部变异策略对种群最优值 gbest进行变异操作，具体如式（10-14）所示：
式中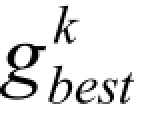 
── 全局最优解在第k 维的取值；
η～Gauss(0,1)。