1.3 例题解析
2025年10月13日
1.3 例题解析
例1-1 试求如图1-1所示结构中1—1和2—2两截面上的内力。
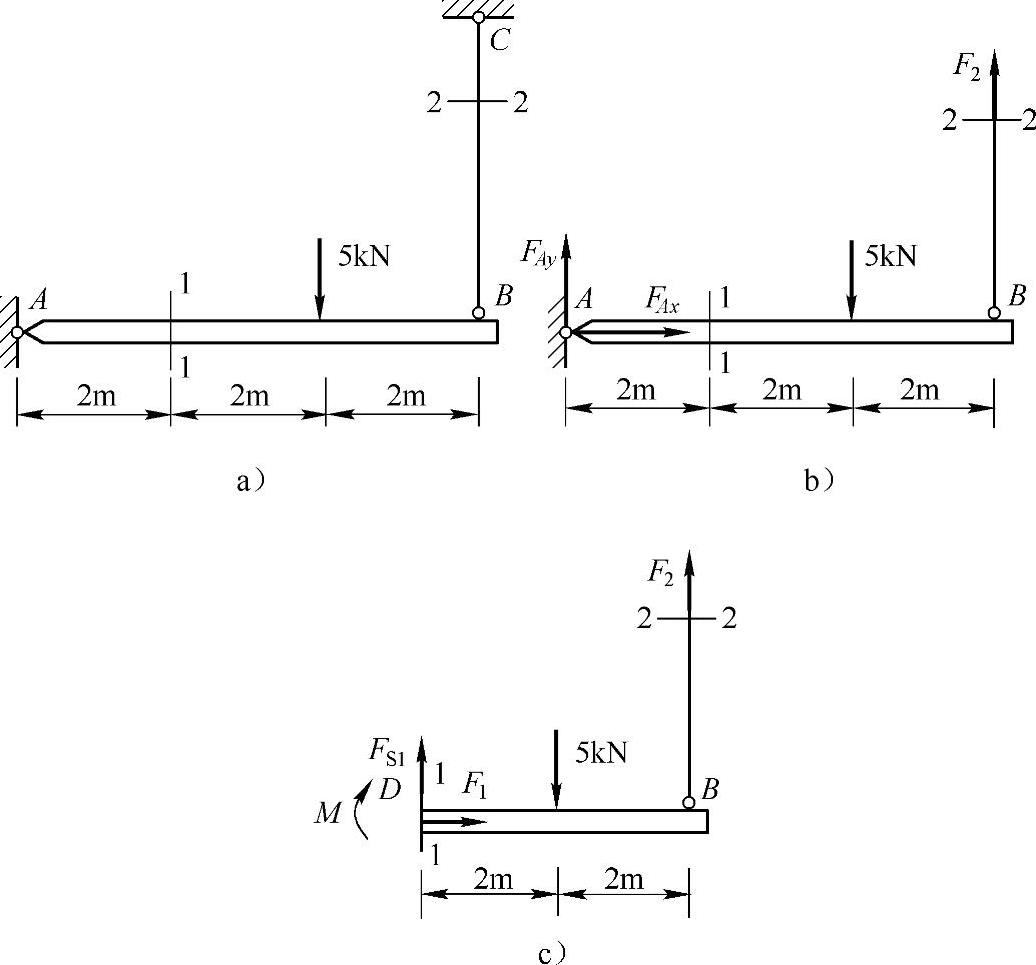
图1-1 例1-1图
解:(1)计算2—2截面内力。应用截面法,对图1-1a取截面2—2以下部分为研究对象,受力图如图1-1b所示,由平衡条件
ΣMA=0,F2×6m-5kN×4m=0
解得 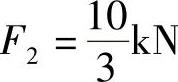
(2)计算1—1截面内力。应用截面法,对图1-1a取截面2—2以下及1—1以右部分为研究对象,受力图如图1-1c所示,由平衡条件得
ΣMD=0,F2×4m-5kN×2m-M=0 (1)
ΣFx=0,F1=0 (2)
ΣFy=0,FS1+F2-5kN=0 (3)
将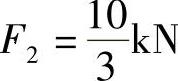 代入式(1)、式(3)两式,解得
代入式(1)、式(3)两式,解得
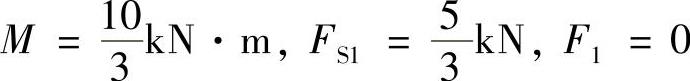
例1-2 如图1-2所示的三角形薄板因受外力作用而变形,角点B垂直向上的位移为0.045mm,但AB和BC仍保持为直线。试求沿OB的平均应变,并求AB与BC两边在B点的角度改变。
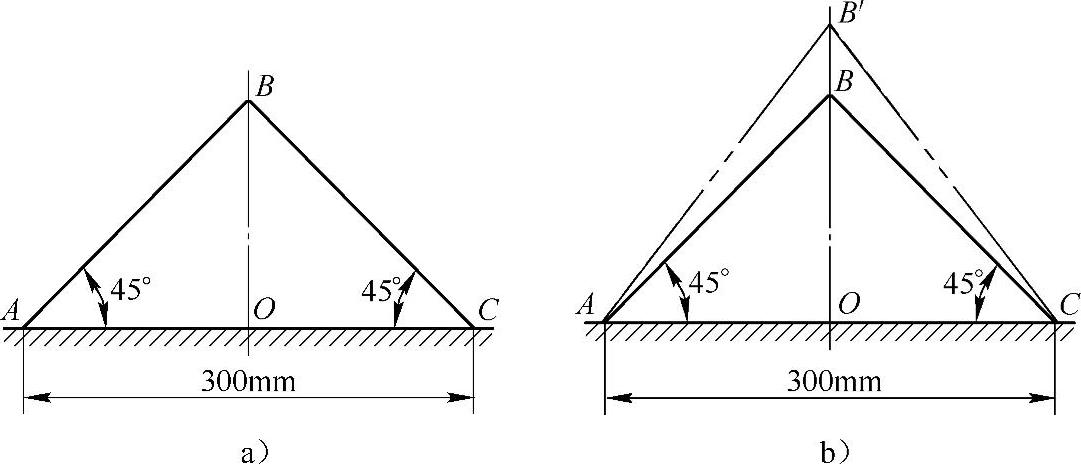
图1-2 例1-2图
解:由线应变的定义可知,沿OB的平均应变为
εm =(OB′-OB)/OB=0.045mm/150mm=3×10-4
由角应变定义可知,B点的角应变为