9.3  例题解析

9.3 例题解析

例9-1 图9-2所示两桁架中各杆的材料和截面均相同，设F₁和F₂分别为这两个桁架稳定的最大载荷，试比较F₁和F₂的大小。

解：图9-2a中，AD杆受压，由

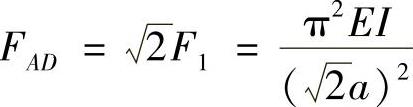
解得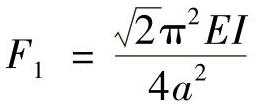

图9-2b中，AB杆受压，由

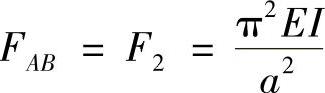
解得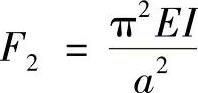

所以F₂＞F₁

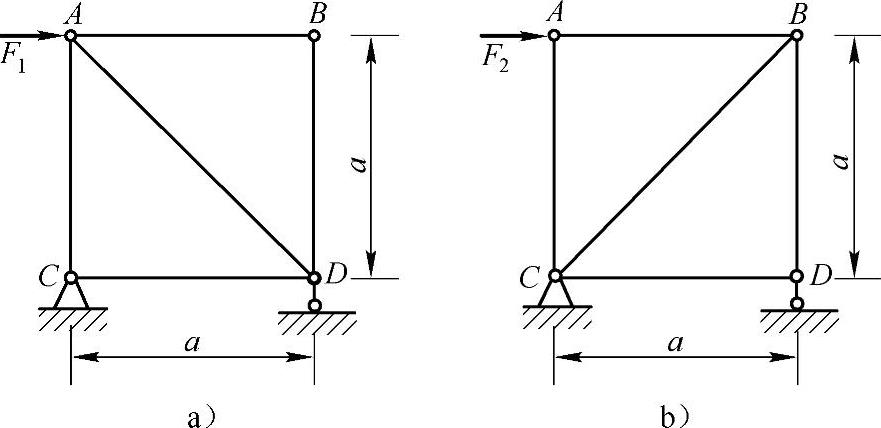
图9-2 例9-1图

例9-2 如图9-3所示，长方形截面细长压杆，b/h=1/2；如果将b改为h后仍为细长杆，临界力F_cr是原来的多少倍？

解：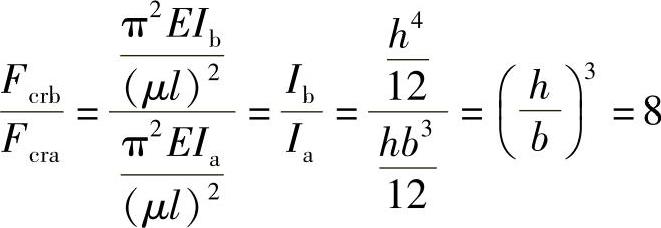

例9-3 圆截面的细长压杆，材料、杆长和杆端约束保持不变，若将压杆的直径缩小为原来的1/2，则其临界力为原压杆的多少倍？若将压杆的横截面改变为面积相同的正方形截面，则其临界力为原压杆的多少倍？

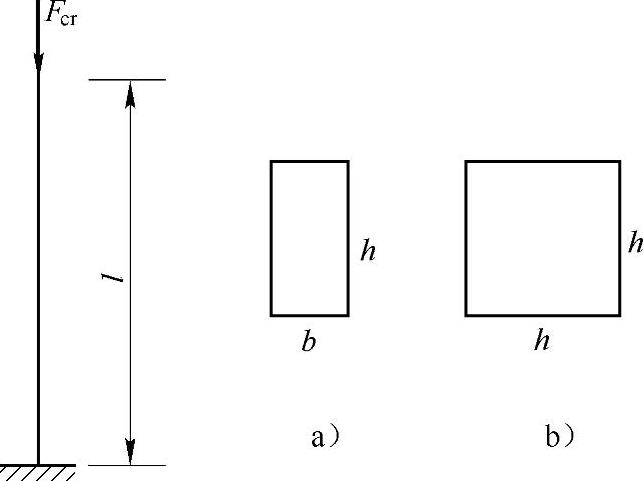
图9-3 例9-2图

解：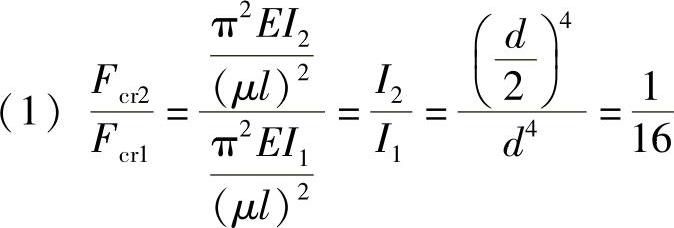

故临界力为原压杆的。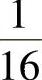

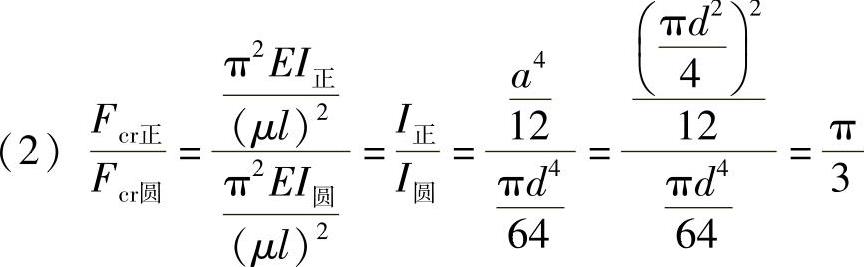
故临界力为原压杆的。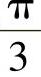

例9-4 五根直径都为d的细长圆杆铰接构成平面正方形杆系ABCD，如果各杆材料相同，弹性模量为E。求图9-4a、b所示两种载荷作用下杆系所能承受的最大载荷。

解：a）杆BD受压，其余杆受拉。

BD杆的临界压力为

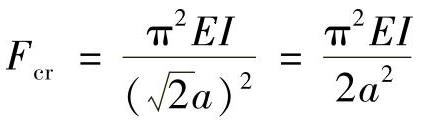
故杆系所能承受的最大载荷为

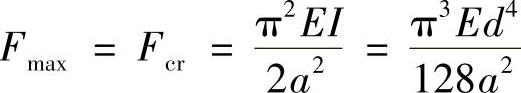
b）杆BD受拉，其余杆受压。

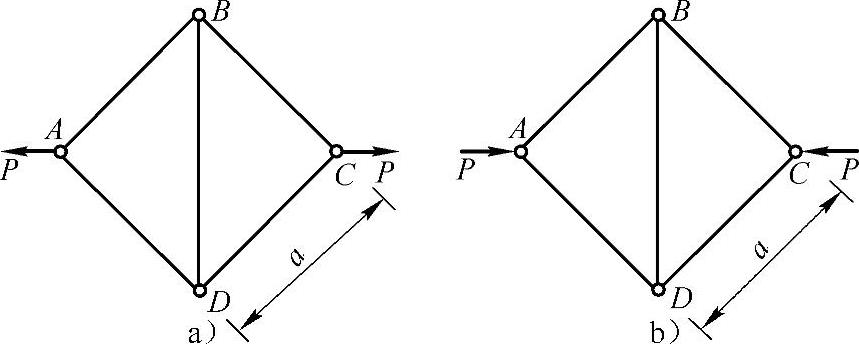
图9-4 例9-4图

四根受压杆的临界压力为

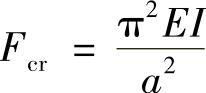
故杆系所能承受的最大载荷为

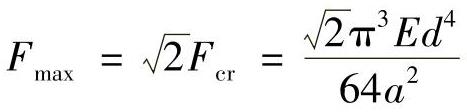
例9-5 图9-5所示结构中，1，2两杆截面和材料相同，均为细长压杆。确定使载荷F为最大值时的θ角（设0＜θ＜π/2）。

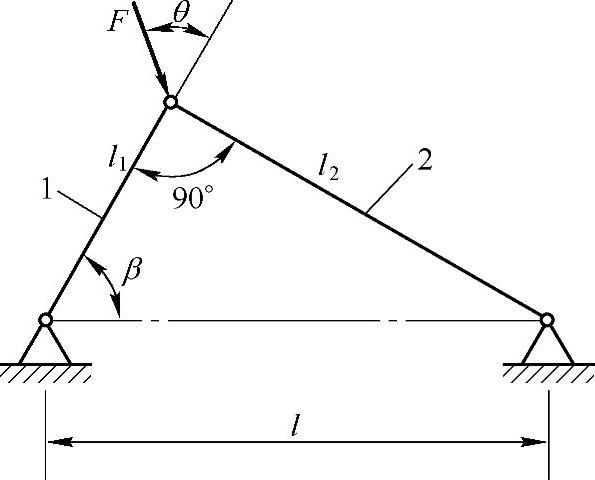
图9-5 例9-5图

解：由静力平衡条件可解得两杆的压力分别为

F₁=Fcosθ，F₂=Fsinθ

两杆的临界压力分别为

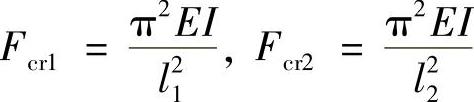
要使F最大，只有F₁，F₂达到临界压力，即

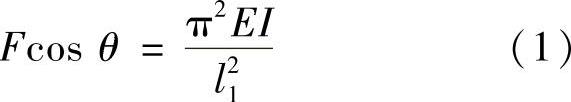
将式（2）除以式（1），得

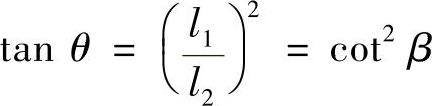
由此得

θ=arctan（cot²β）

例9-6 松木制成的受压柱，矩形横截面为b×h=100mm×180mm，弹性模量E=10GPa，λ_p=110，杆长l=7m。在xz平面内失稳时（绕y轴转动），杆端约束为两端固定（图9-6a），在xy平面内失稳时（绕z轴转动），杆端约束为两端铰支（图9-6b）。求木柱的临界应力和临界力。

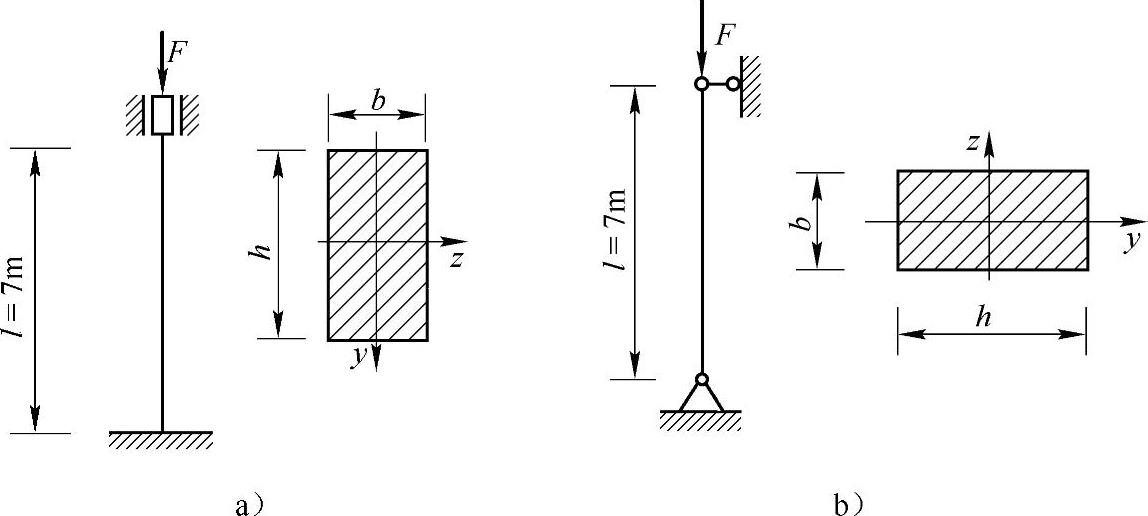
图9-6 例9-6图

解：（1）在xz（最小刚度）平面内的临界应力和临界力。

此时μ_y=0.5，横截面对y轴的惯性半径为

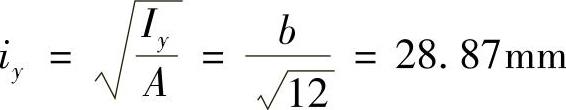
在此平面内，

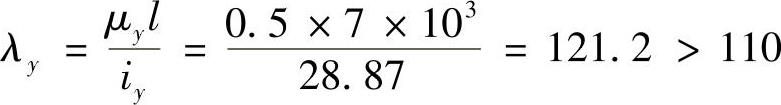
符合欧拉公式的适用条件。临界应力为

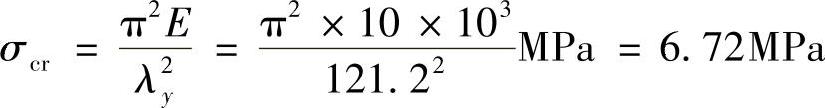
临界力为

F_cr=σ_crA=（6.72×100×180×10^-3）kN=121kN

（2）在xy（最大刚度）平面内的临界应力和临界力。

此时μ_y=1.0，横截面对z轴的惯性半径为

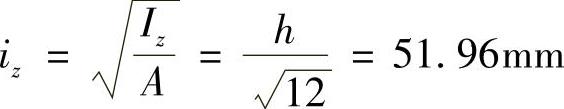
在此平面内，

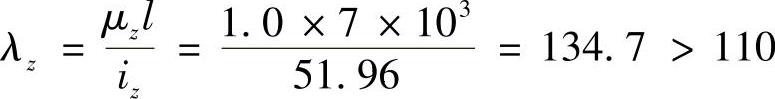
符合欧拉公式的适用条件。临界应力为

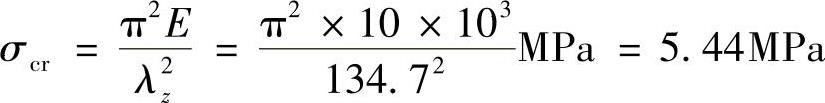
临界力为

F_cr=σ_crA=（5.44×100×180×10^-3）kN=97.9kN

例9-7 图9-7a所示结构中，分布载荷q=20kN/m。梁的截面为矩形，b=90mm，h=130mm。立柱的截面为圆形，直径d=80mm。梁和柱均为Q235钢，[σ]=160MPa，E=206GPa，σ_p=200MPa，稳定安全因数n_st=3。试校核结构的安全。

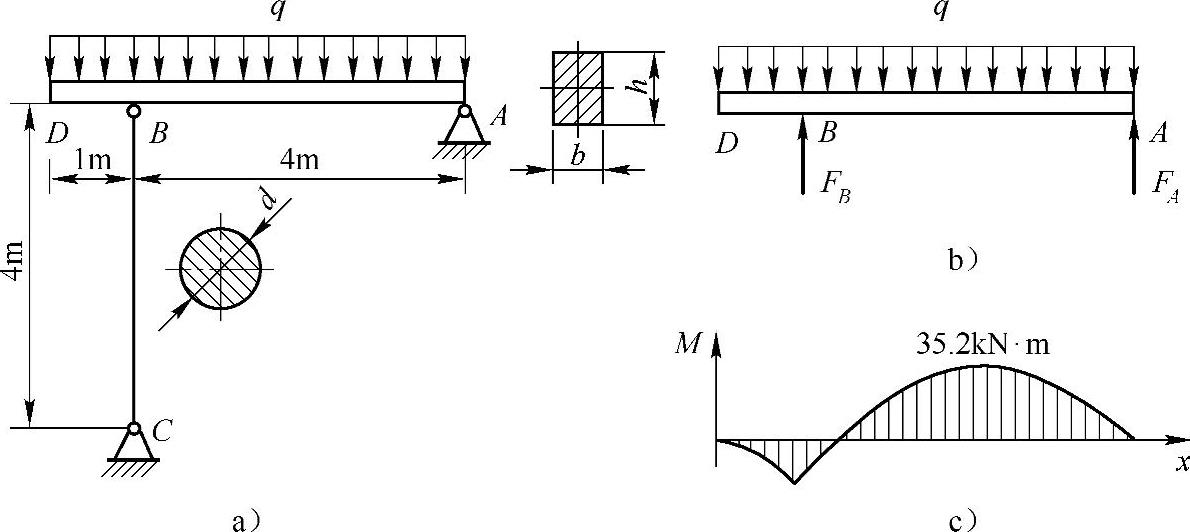
图9-7 例9-7图

解：（1）校核梁的强度。

根据图9-7b所示，由ΣM_A=0得

F_B =62.5kN

作梁的弯矩图，如图9-7c所示，则由图可知

M_max =35.2kN·m

梁的最大弯曲正应力为

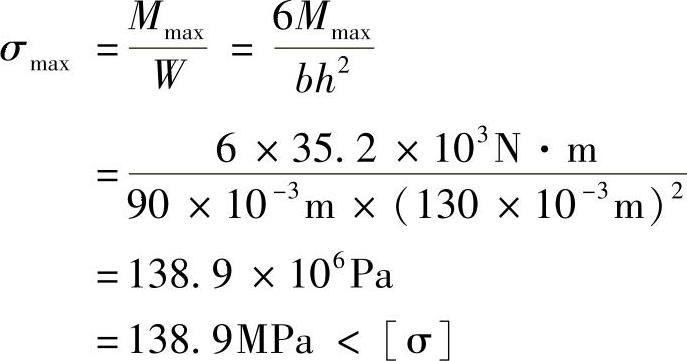
所以梁的强度足够。

（2）立柱的稳定性校核。

立柱的轴向压力为F=F_B=62.5kN，柱两端铰支，则

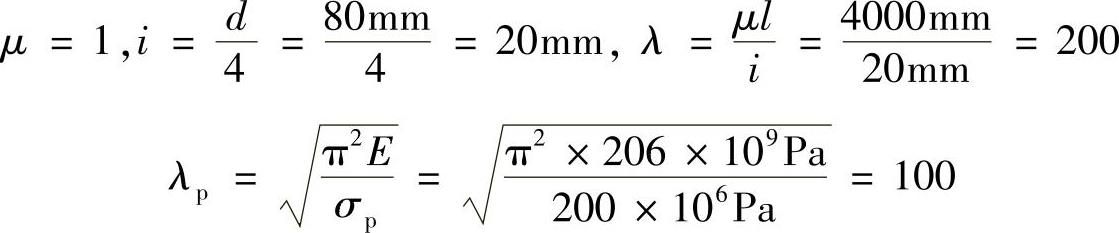
λ＞λ_p，故BC杆是大柔度杆。从而有

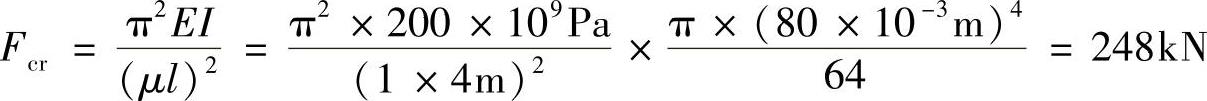
稳定校核

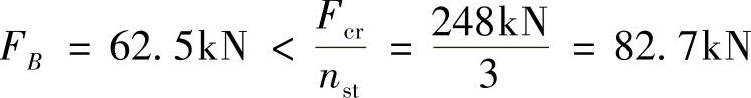
柱的稳定性足够，所以结构安全。

例9-8 图9-8所示工字钢直杆在温度t₁=20℃时安装，此时杆不受力，已知杆长l=6m，材料为Q235钢，E=200GPa。试问当温度升高到多少摄氏度时杆将失稳？（材料的线胀系数α=12.5×10^-6K^-1）。

图9-8 例9-8图

解：（1）确定工字钢的柔度。

工字钢的两端固定，则

μ=0.5

查型钢表得NO.20a工字钢的惯性半径为

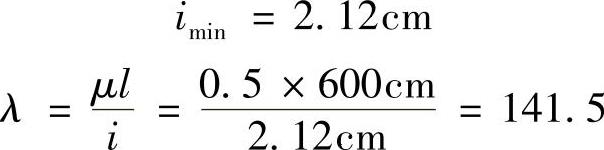
此工字钢杆属细长杆。则

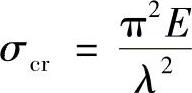
（2）当温度升高Δt℃时，杆中应力为

σ_t=αEΔt≤σ_cr，即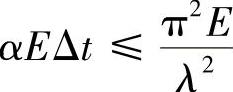

故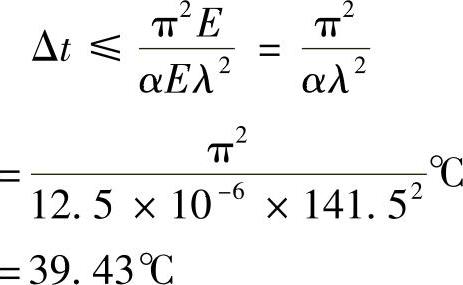

例9-9 如图9-9a所示托架中的AB杆为圆截面直杆，直径d=40mm，长度l=800mm，其两端可视为A3钢，试求：（1）AB杆的临界载荷F_cr；（2）若已知工作载荷F=70kN，AB杆规定的稳定安全因数n_st=2，问此托架是否安全？

解：（1）计算压杆柔度，判断压杆类型。

圆截面的惯性半径为

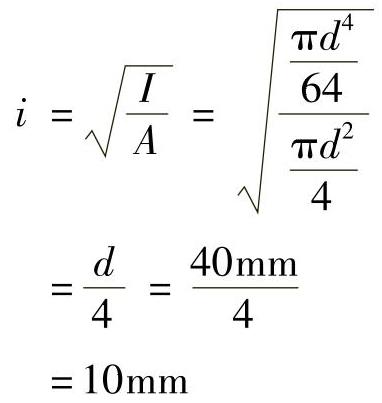
压杆两端铰支，则

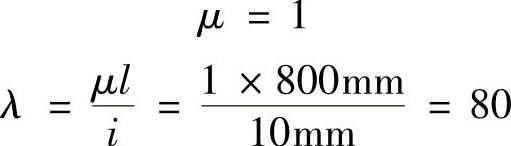
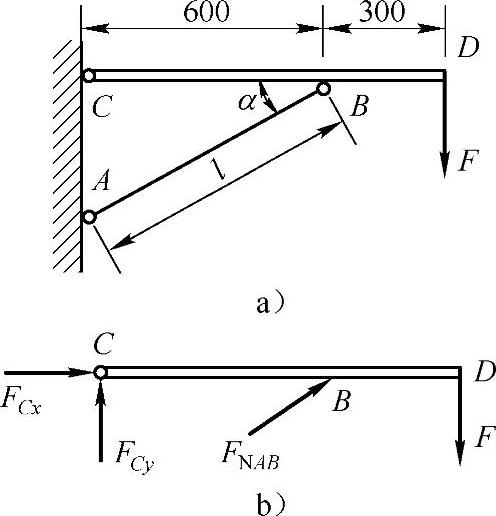
图9-9 例9-9图

λ_s＜λ＜λ_p，故AB杆为中柔度杆，所以临界力为

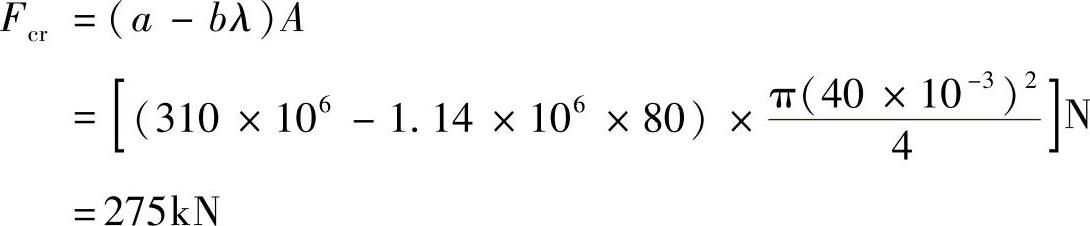
（2）取杆CBD为研究对象，如图9-9b所示由ΣM_C=0，有

（300mm+600mm）F-F_NABsinα×600mm=0

因为

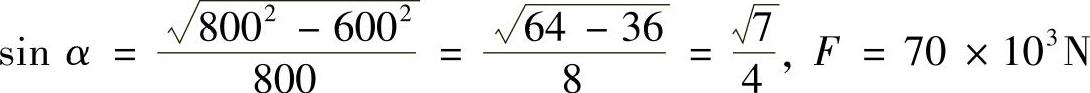
所以

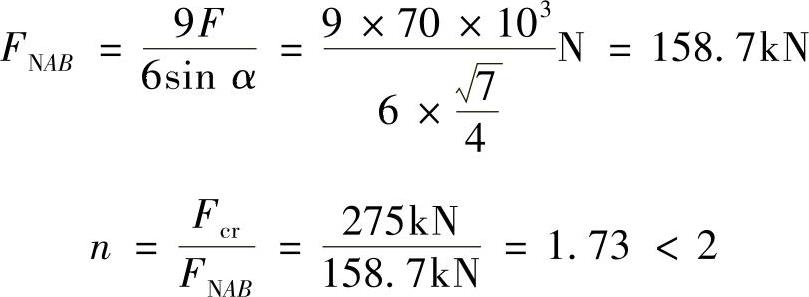
由上可知：AB杆稳定性不够，故此托架不安全。