7.3  例题解析

7.3 例题解析

例7-1 从构件中取出的微元受力如图7-6所示，其中AC为自由表面（无外力作用）。试求σ_x和τ_xy。

解：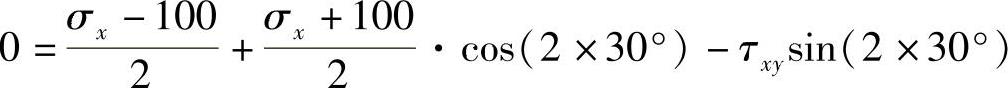

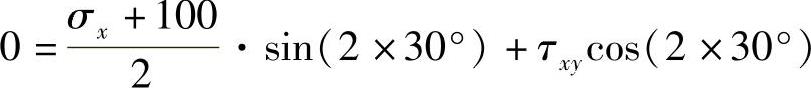
联立方程解得 σ_x=-33.3MPa

τ_xy=-τ_yx=-57.7MPa

例7-2 已知应力状态如图7-7所示（应力单位为MPa），试用解析法计算图中指定截面的正应力和切应力。

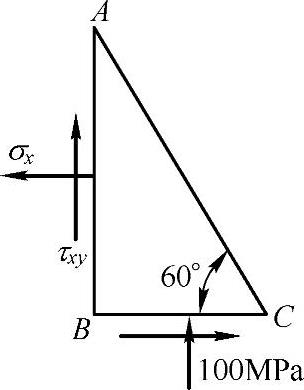
图7-6 例7-1图

解：a）由题图所示应力状态可知

σ_x=30MPa，σ_y=10MPa，τ_xy=-20MPa，α=45°

将上列数据代入平面应力状态斜截面应力公式，得指定斜截面上的正应力和切应力分别为

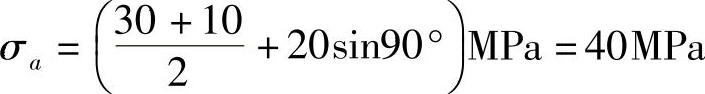
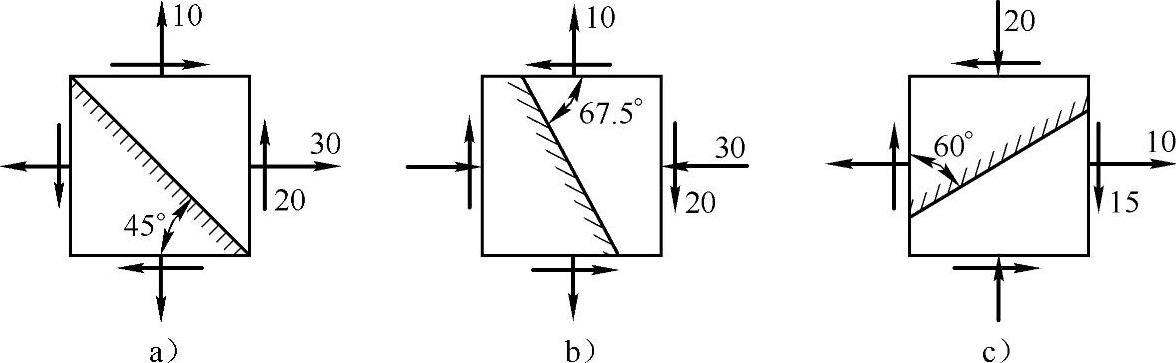
图7-7 例7-2图

b）由题图所示应力状态可知

σ_x=-30MPa，σ_y=10MPa，τ_xy=20MPa，α=22.5°

由此可得指定斜截面上的正应力和切应力分别为

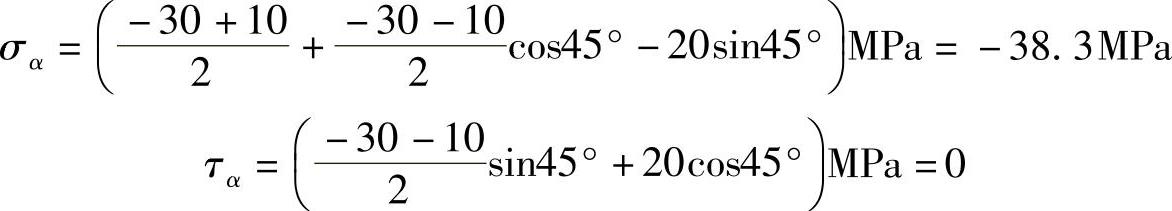
c）由题图所示应力状态可知

σ_x=10MPa，σ_y=-20MPa，τ_x=15MPa，α=-60°

由此可得指定斜截面上的正应力和切应力分别为

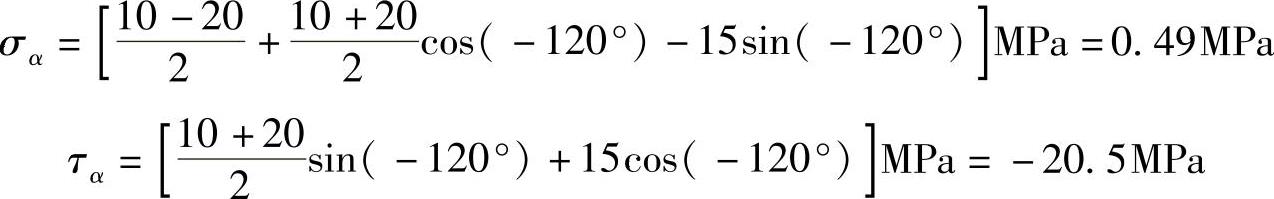
例7-3 试确定图7-8所示应力状态中的最大正应力和最大切应力。图中应力的单位为MPa。

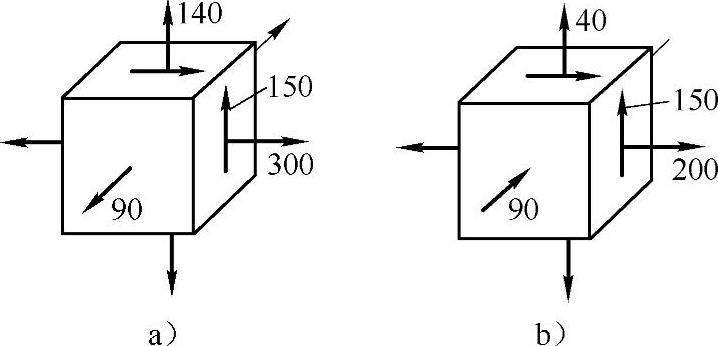
图7-8 例7-3图

解：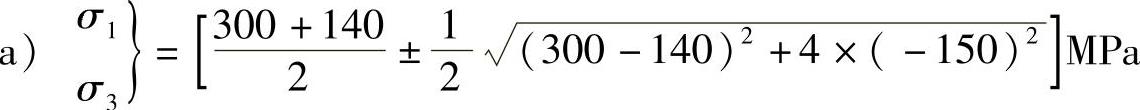

例7-4 图7-9所示矩形板，承受正应力σ_x与σ_y作用，试求板厚的改变量Δδ与板件的体积改变量ΔV。已知板件厚度δ=10mm，宽度b=800mm，高度h=600mm，正应力σ_x=80MPa，σ_y=-40MPa，材料为铝，弹性模量E=70GPa，泊松比μ=0.33。

解：此为平面应力状态问题。设板厚度方向的正应力为ε_z，则有

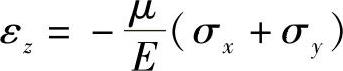
板厚的改变量为

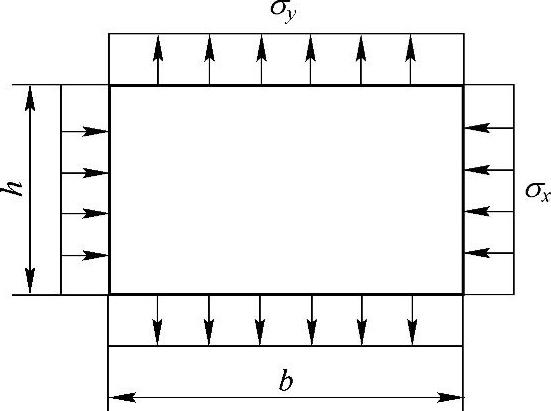
图7-9 例7-4图

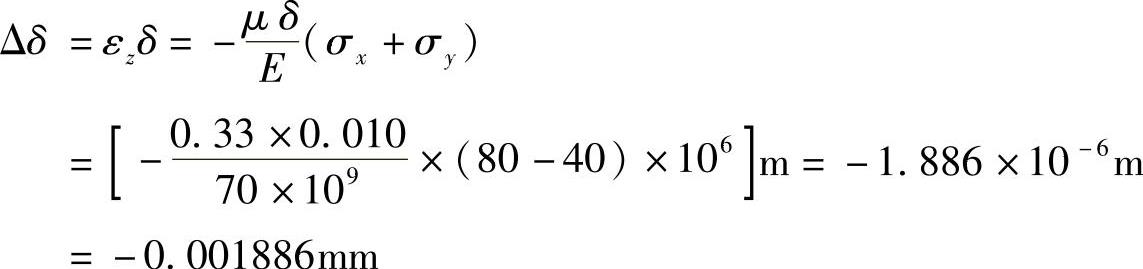
体应变为

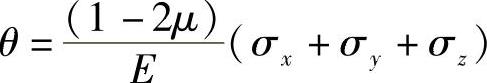
由此可得该板件的体积改变量为

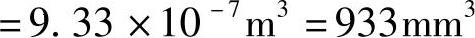
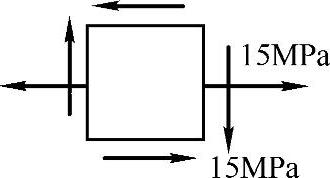
图7-10 例7-5图

例7-5 从某铸铁构件内的危险点处取出的单元体，各面上的应力分量如图7-10所示。已知铸铁材料的泊松比_μ=0.25，许用拉应力[σ_t]=30MPa，许用压应力[σ_c]=90MPa。试按第一和第二强度理论校核其强度。

解：主应力

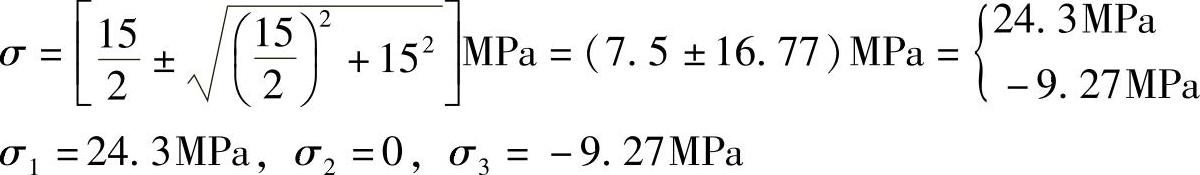
按第一强度理论：σ_r1=σ₁＜[σ_t]，安全；

按第二强度理论：σ_r2=σ₁-μ（σ₂+σ₃）=[24.3-0.25×（0-9.27）]MPa＜[σ_t]，安全。

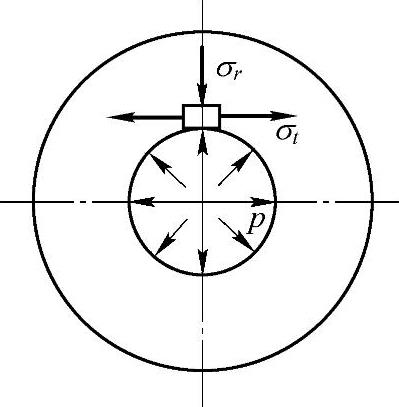
图7-11 例7-6图

例7-6 某厚壁筒横截面如图7-11所示。在危险点处，σ_t=500MPa，σ_r=-350MPa，第三个主应力垂直于图面是拉应力，且其数值为420MPa。试按第三和第四强度理论计算其相当应力。

解：（1）危险点处的主应力为

σ₁=500MPa，σ₂=420MPa，σ₃=-350MPa

（2）按第三强度理论计算其相当应力为

σ_r3=σ₁-σ₃=500MPa+350MPa=850MPa

（3）按第四强度理论计算其相当应力为

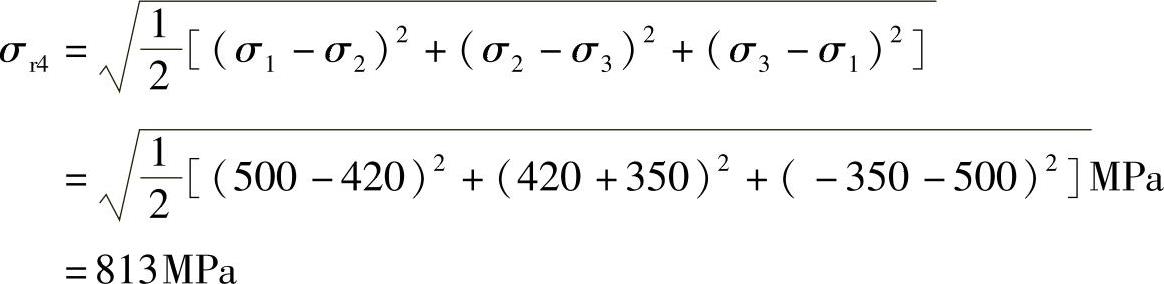
例7-7 图7-12所示悬臂梁，承受载荷F=20kN作用，试绘微体A，B与C的应力图，并确定一应力的大小及方位。

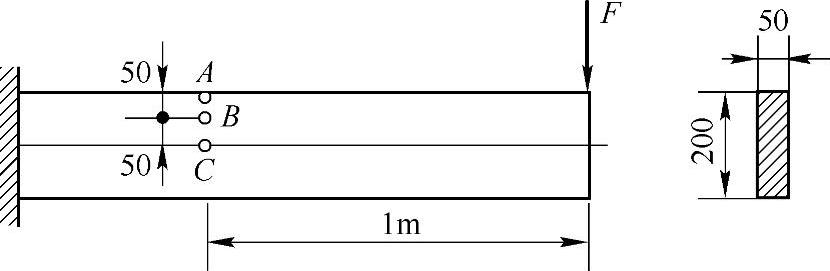
图7-12 例7-7图

解：由题图可知，指定截面的剪力、弯矩分别为

F_S=F=20kN，|M|=Fa=20kN×1m=20kN·m

微体A，B和C的应力图依次如图7-13a、b和c所示。

对于应力图7-13a，其正应力

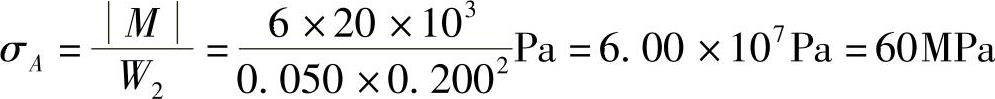
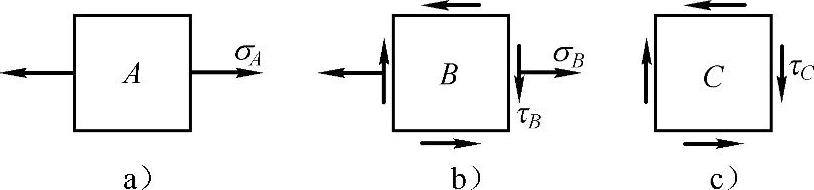
图 7-13

由此可知，主应力为

σ₁=60MPa，σ₂=σ₃=0

σ₁的方位角为

α₀=0

对于应力图7-13b，其正应力和切应力分别为

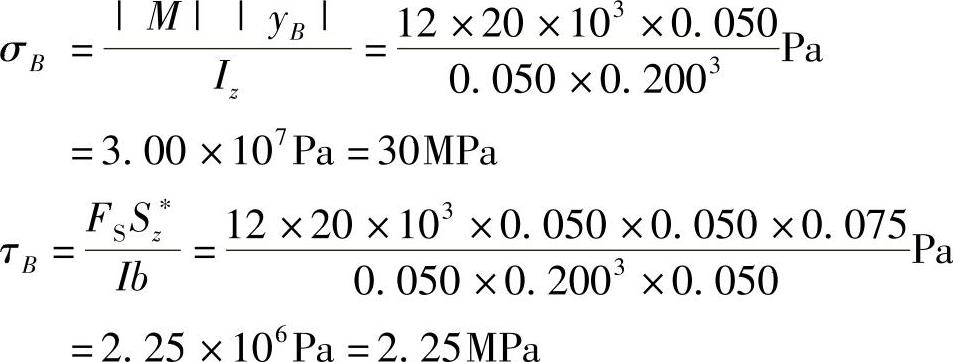
极值应力为

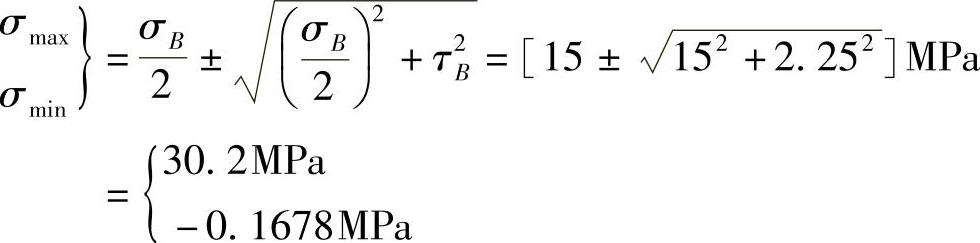
由此可知，主应力为

σ₁=30.2MPa，σ₂=0，σ₃=-0.1678MPa

由

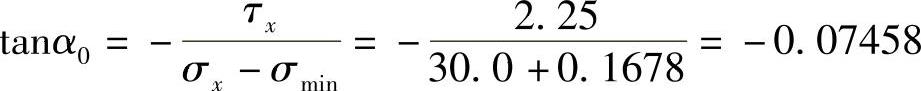
得σ₁的方位角为

α₀=-4.27°

对于应力图7-13c，其切应力为

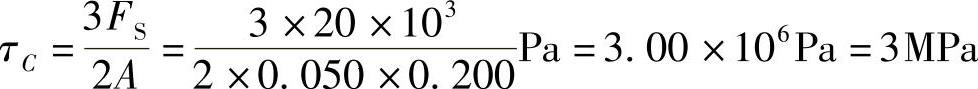
由此得各主应力依次为

σ₁=3MPa，σ₂=0，σ₃=-3MPa

σ₁的方位角为

α₀=-45°