2.3 例题解析
例2-1 一木柱受力如图2-1a所示,柱的横截面是直径为30cm的圆,材料服从胡克定律,其弹性模量E=20GPa,如果不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形。
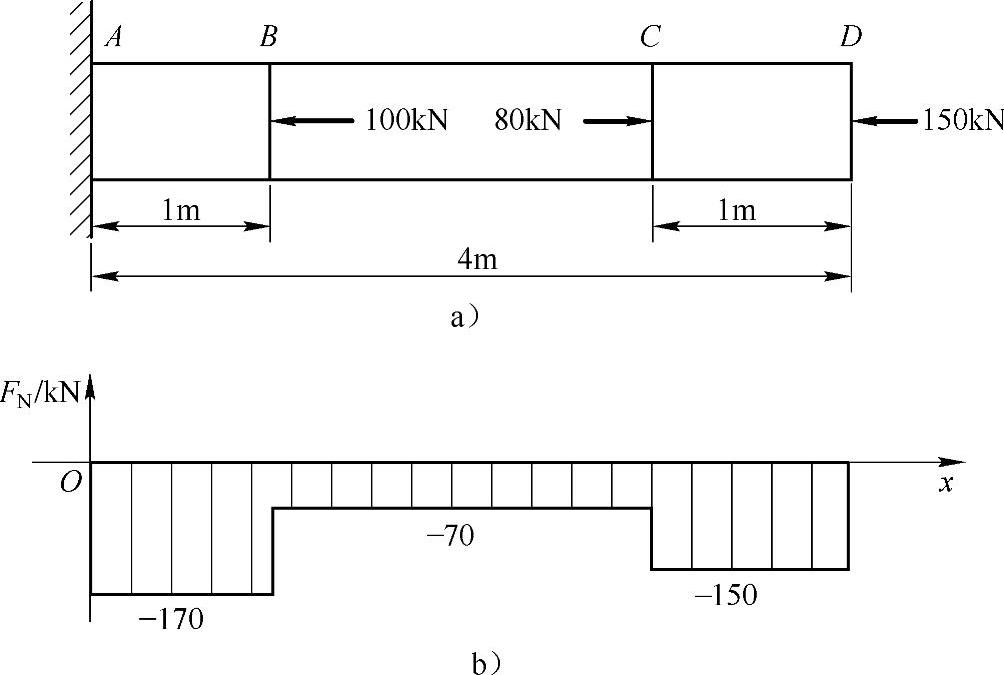
图2-1 例2-1图
解:(1)轴力图如图2-1b所示。
(2)AB段应力: 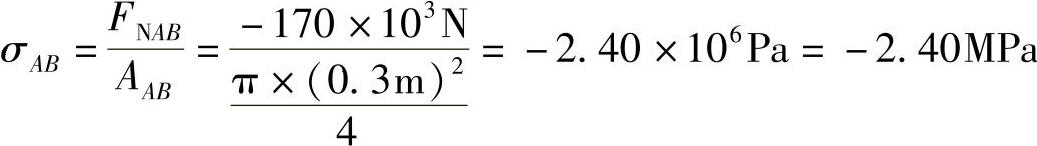
BC段应力: 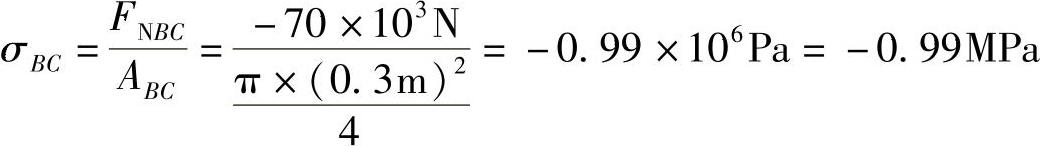
CD段应力: 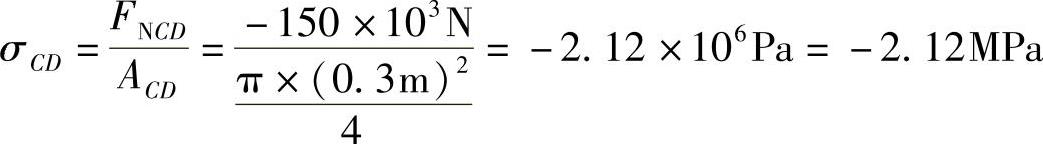
(3)AB段线应变: 
BC段线应变: 
CD段线应变: 
(4)柱的总变形为
ΔAD=ΔAB+ΔBC+ΔCD=εABlAB+εBClBC+εCDlCD
=-1.2×10-4×1m-4.95×10-5×2m-1.06×10-4×1m
=-3.25×10-4m
例2-2 图2-2所示拉杆沿斜截面m—n由两部分胶合而成,设在胶合面上许用拉应力[σ]=100MPa,许用切应力[τ]=50MPa。并设胶合面的强度控制杆件的拉力,试问:为使杆件承受最大拉力F,α角的值应为多少?若横截面面积为4cm2,并规定α≤60°,试确定许用载荷[F]。
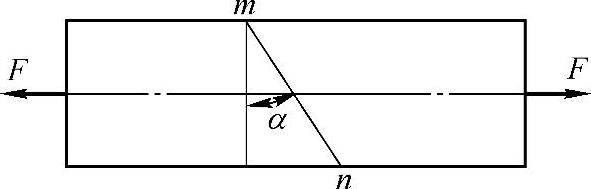
图2-2 例2-2图
解:由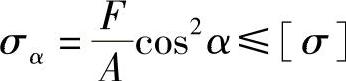 及
及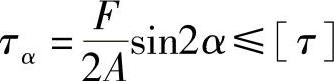 ,得
,得
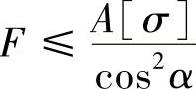 且
且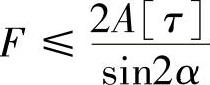
所以为使F最大,则应满足 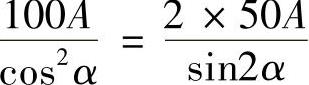
解得tanα=1/2,即α=26.6°。
当α=60°且A=4cm2时,有
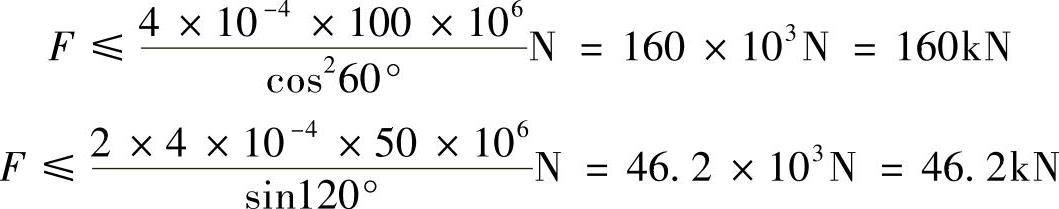
所以[F]=46.2kN。
例2-3 求图2-3所示各简单结构中节点A的位移,设各杆的抗拉(压)刚度均为EA。
解:(1)AB杆内力为零,AC杆内力为F,则
AB杆变形: ΔlAB=0
AC杆变形: 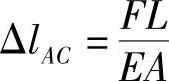
A点位移如图2-3c所示,A1点为A点的最终位置。
其中|AA2|=ΔlAC,A点的位移为
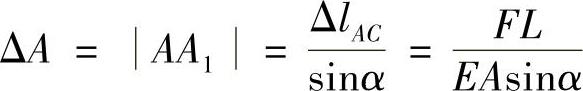
(2)AD杆内力为零,所以
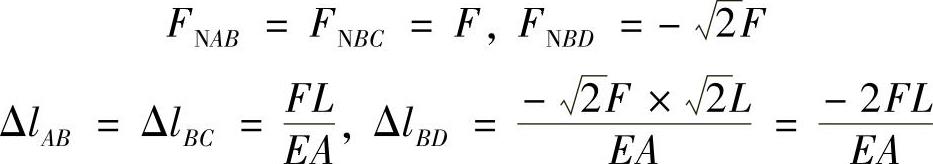
B点和A点的位移如图2-3d所示,点B3和点A3分别为B点和A点的最终位置,则由图可知,A点的位移ΔA=|AA3|=|B1B3|+|A1A2|,其中
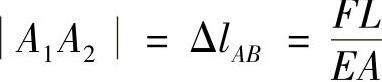
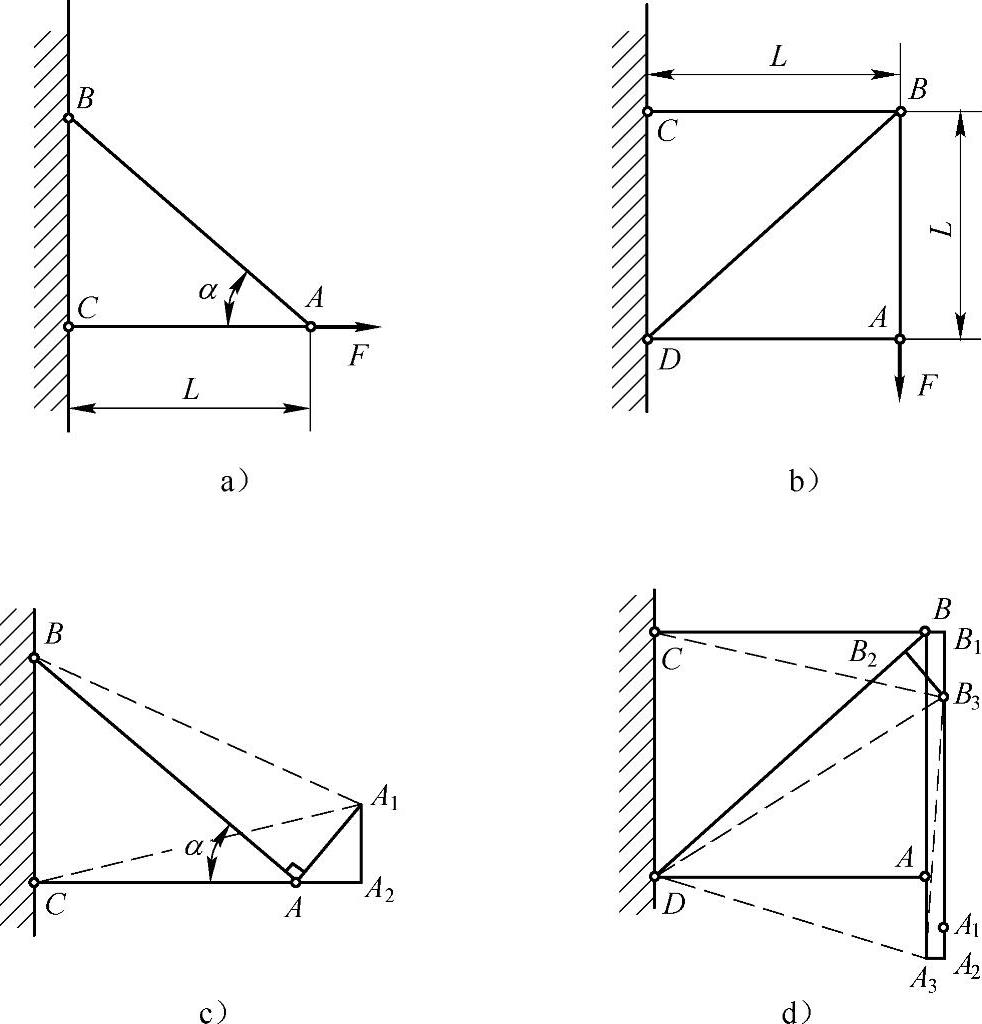
图2-3 例2-3图
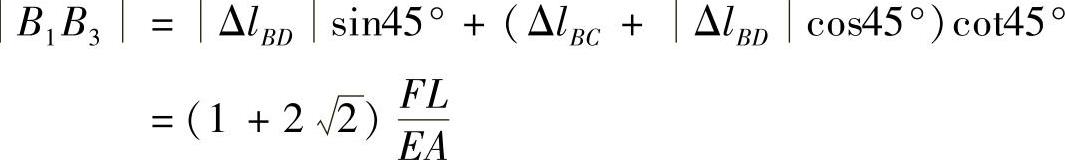
所以 ,方向铅垂向下。
,方向铅垂向下。
例2-4 在图2-4a所示杆系中,节点B处承受铅垂载荷F,斜杆AB的长度为L1,水平杆的长度为L2,两杆的材料相同,且抗拉和抗压许用应力相等,同为[σ],求为使杆系具有最小重量时的α角。
解:(1)选取节点B为研究对象,则受力分析如图2-4b所示。
由平衡条件
ΣFy=0,FABsinα=F
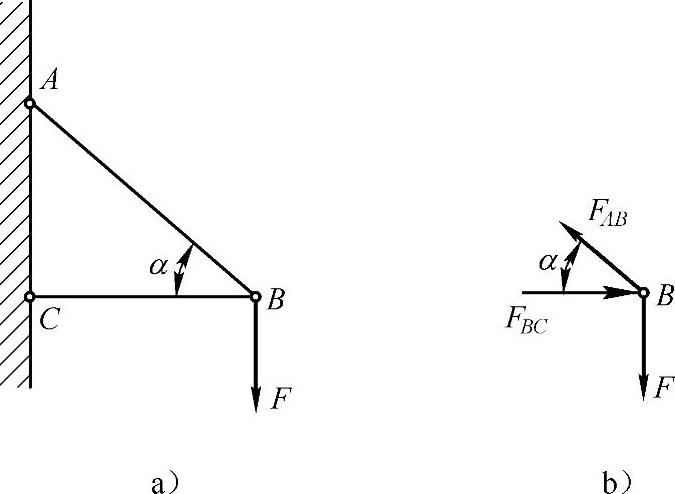
图2-4 例2-4图
ΣFx=0,FABcosα=FBC
得 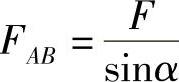 ,
,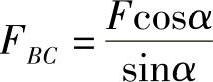
(2)若使两杆的应力均达到材料的许用应力值[σ],则有FN/A=[σ],即
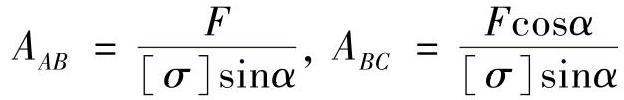
由题意可得,斜杆AB的长度为
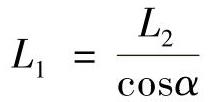
结构的重量为最轻,即结构所用材料的体积V为最小。且
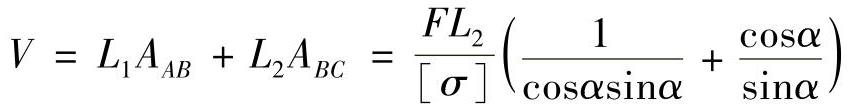
若V最小,则应有dV/dα=0,即
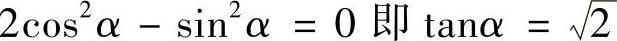
所以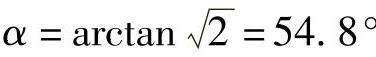 。
。
例2-5 求如图2-5a所示杆的应变能(EA为已知)。
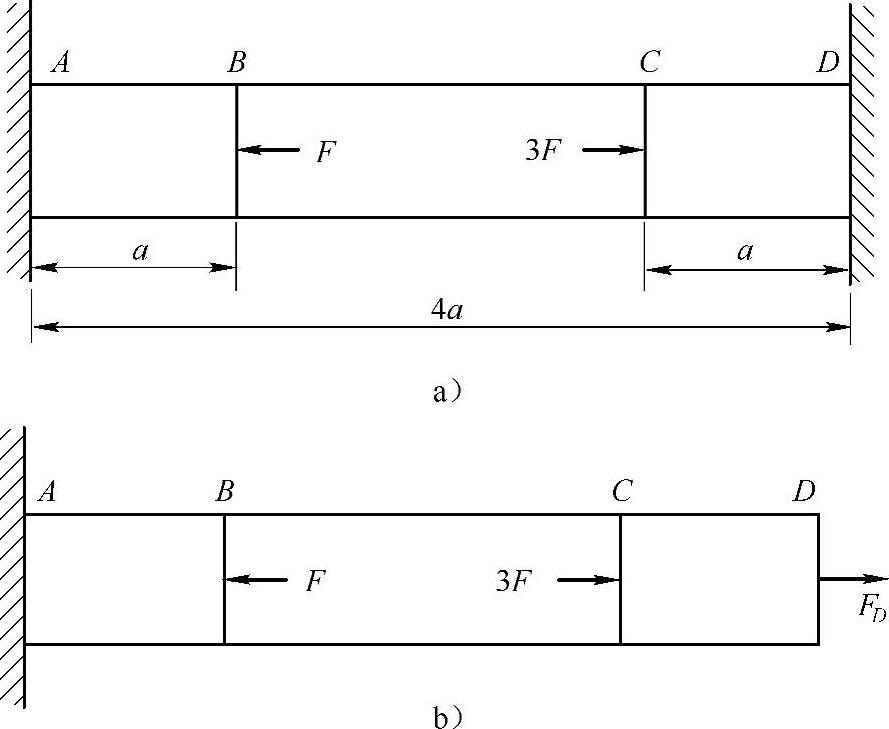
图2-5 例2-5图
解:去掉D支座多余约束,以FD代替,如图2-5b所示。各段内力为
FCD=FD,FBC=3F+FD,FAB=2F+FD
由变形条件 ΔlAB+ΔlBC+ΔlCD=0
代入物理条件 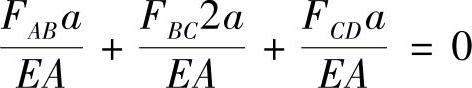
得 (2F+FD)a+(3F+FD)×2a+FDa=0
所以 FD=-2F
则 FCD=-2F,FBC=F,FAB=0
则杆件应变能为 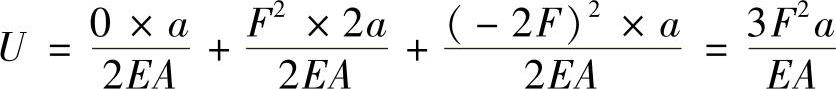
例2-6 某结构如图2-6所示,其中的横梁ABC可看做刚体,它由钢杆1,2支承,杆1的长度做短了δ=3×10-3l,两杆的截面积均为A=2cm2,弹性模量E=200GPa,线胀系数α=12.5×10-6K-1,试求:(1)装配后各杆横截面上的应力;(2)装配后温度需要改变多少才能消除初应力?
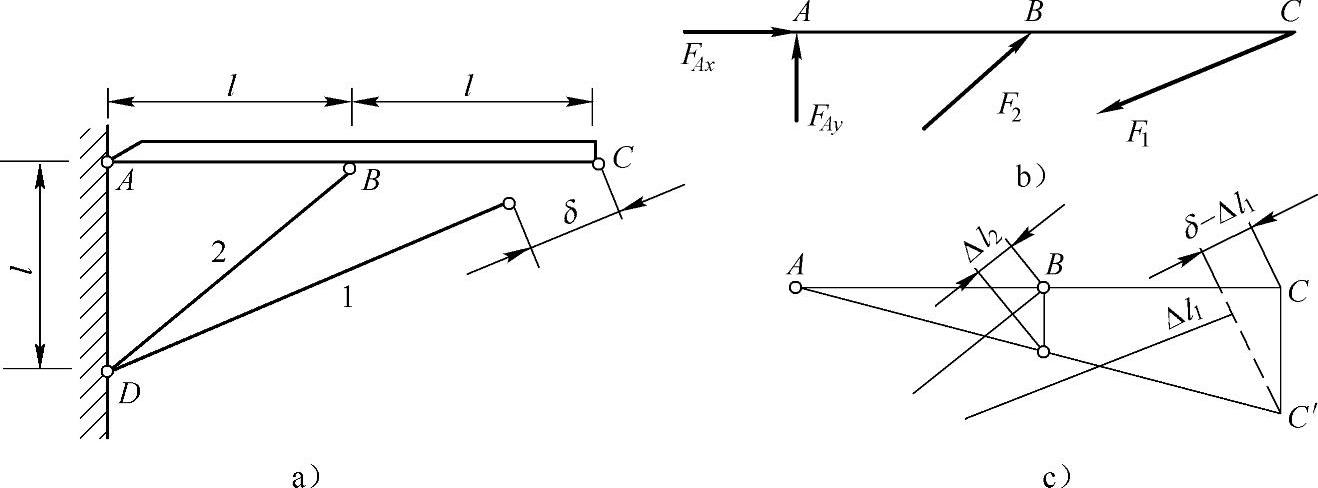
图2-6 例2-6图
解:(1)设∠DCA=θ。
由静力平衡方程 ΣMA=0,F1×2lsinα=F2×lsin45°
变形协调方程 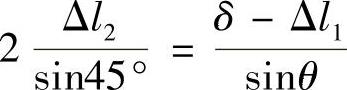
联立求解得到 F1=2.96kN,F2=-37.56kN
则 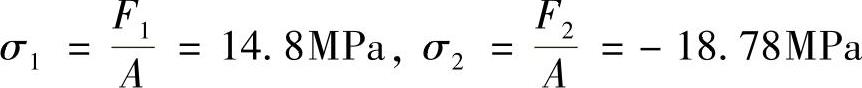
(2)由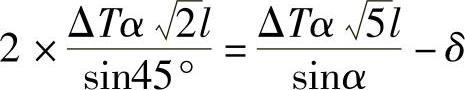 解得ΔT=59.63K=59.63℃时,初应力为零。
解得ΔT=59.63K=59.63℃时,初应力为零。
例2-7 刚性横梁AB悬挂于三根平行杆上,如图2-7a所示。l=2m,F=40kN,a=1.5m,b=1m,c=0.25m,δ=0.2mm。杆1由黄铜制成,A1=2cm2,E1=100GPa,α1=16.5×10-6K-1,杆2和杆3由碳钢制成,A2=1cm2,A3=3cm2,E2=E3=200GPa,α2=α3=12.5×10-6K-1,设温度升高20℃,试求此时各杆的应力。
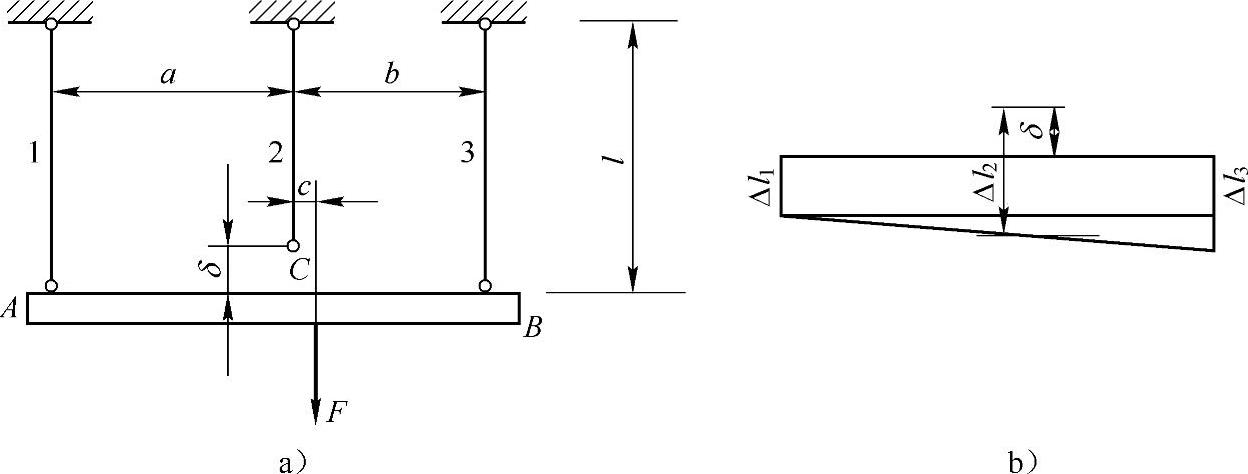
图2-7 例2-7图
解:由平衡条件
ΣFy=0,F1+F2+F3-F=0
ΣMC=0,F1a-F3b+Fc=0
以及变形协调方程(图2-7b)
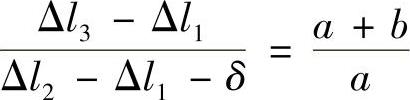
其中 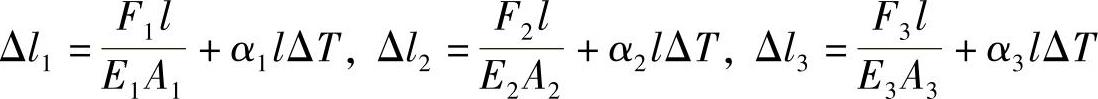
则 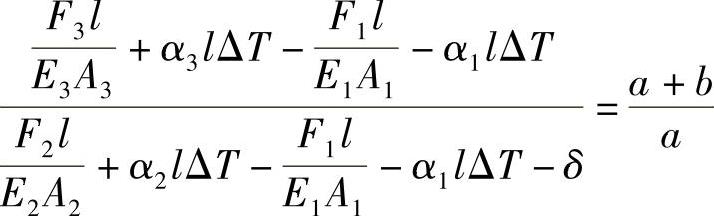
得
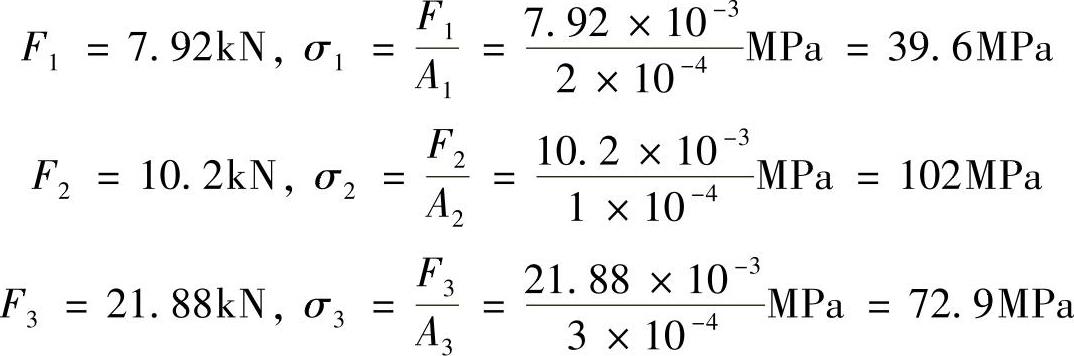
例2-8 一木质拉杆接头部分如图2-8所示,接头处的尺寸为h=b=18cm,材料的许用应力[σ]=5MPa,[σbs]=10MPa,[τ]=2.5MPa,求许用拉力[F]。
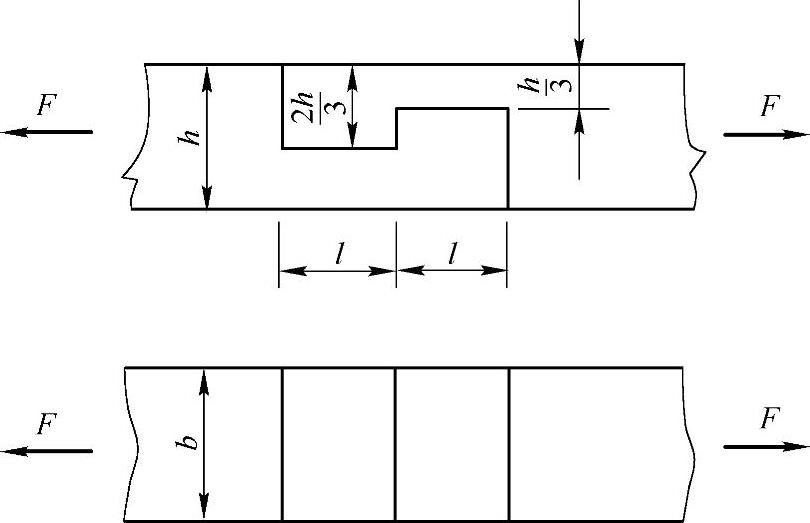
图2-8 例2-8图
解:按剪切强度计算,有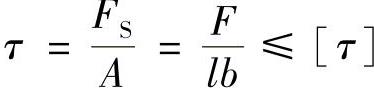
则 F≤[τ]lb=2.5MPa×(0.18cm)2=81kN
按挤压强度计算,有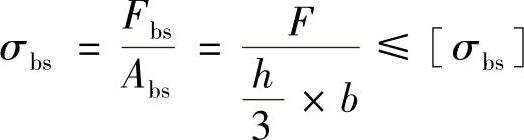
则 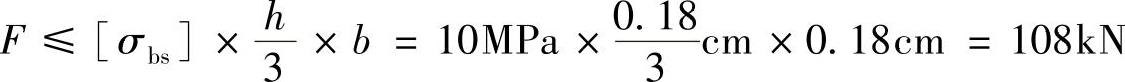
按抗拉强度计算,有 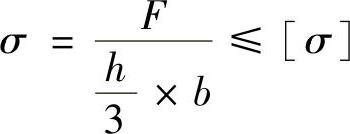
则 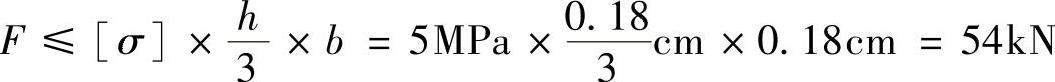
因此,[F]=54kN。
例2-9 图2-9a所示为一钢板条,用九个直径均为d的铆钉固定在立柱上。合力F已知,l=8a(a为铆钉间距)。试求铆钉内的最大切应力。假设:①若作用力通过铆钉群截面的形心,则各铆钉的受力相等。②若作用一力偶,则钢板条有绕铆钉群截面形心C转动的趋势,于是任一铆钉的受力大小与其到形心C的距离成正比,而力的方向与该铆钉至形心C的连线相垂直。
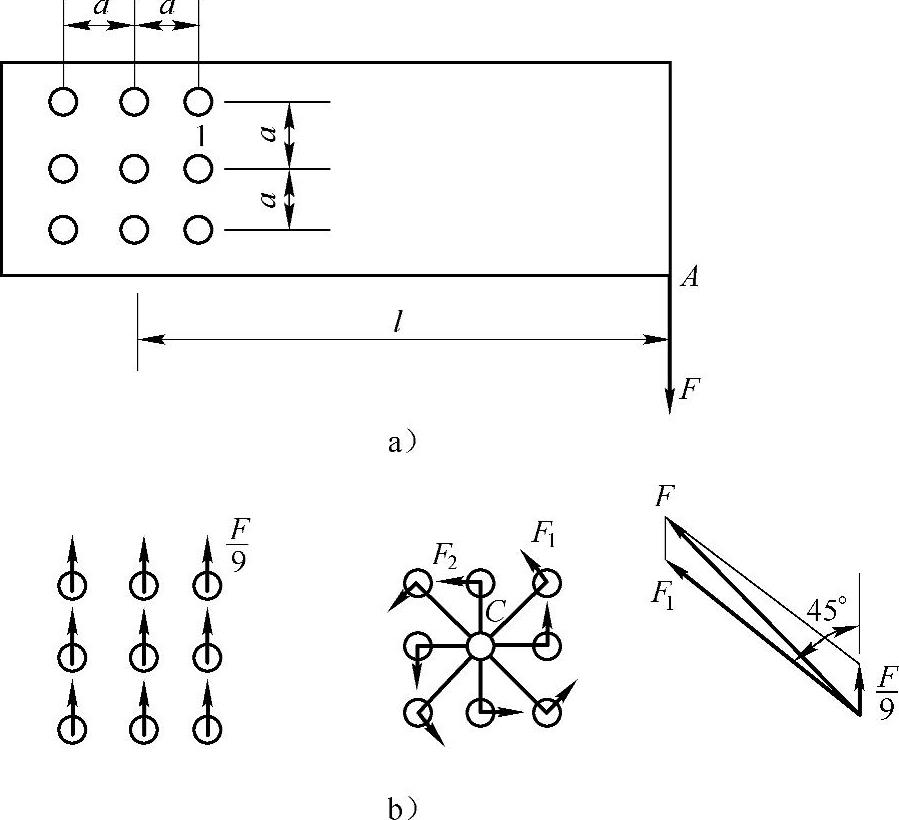
图2-9 例2-9图
解:将A端外力F向铆钉群截面的形心C处简化,得到一个向下的力F和一个顺时针力偶M,其中M=Fl。
力F在铆钉内引起相等的剪力,其值皆为F/9。
由力矩平衡方程 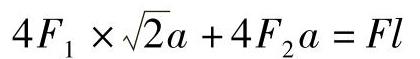
以及 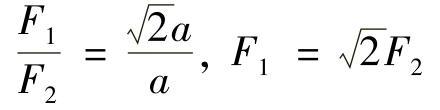
联立解得 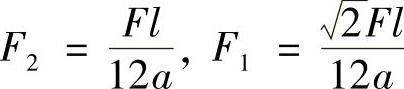
铆钉1最危险,其总剪力为
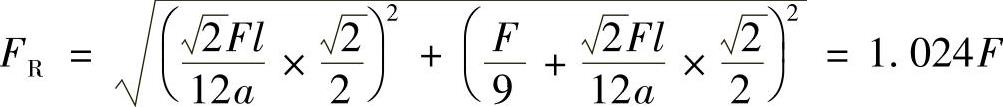
铆钉内的切应力为
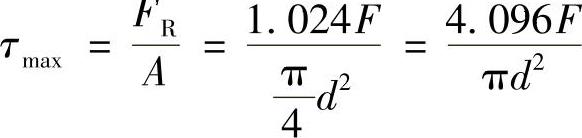
例2-10 如图2-10a所示,已知杆AD,CE,BF的横截面面积均为A,杆材料的许用应力为[σ],梁AB可视为刚体。求结构的许用载荷[F]。
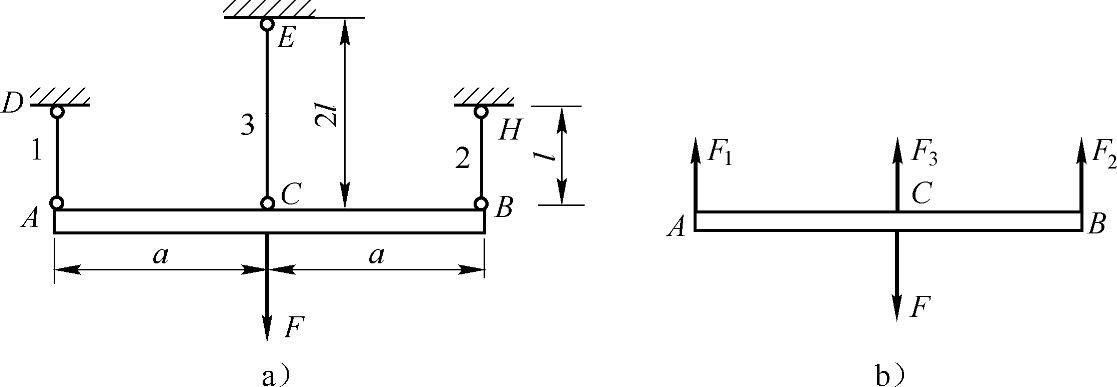
图2-10 例2-10图
解:设杆1、杆2、杆3的内力分别为F1,F2,F3,如图2-10b所示。由于对称,刚性杆AB在外力F作用下有向下的平移,其移动的距离即为各杆的变形,即
Δl1=Δl2=Δl3
根据胡克定律有
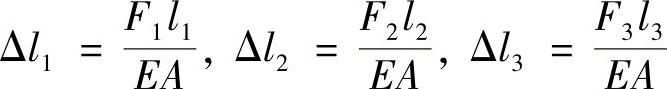
则 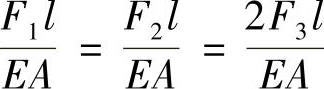
所以 F1=F2=2F3 (a)
又由力的平衡方程,得ΣFy=0,F1+F2+F3=F (b)
联合式(a)、式(b)两式求解,得
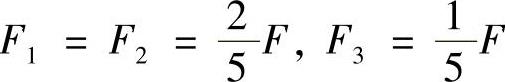
由正应力强度条件知
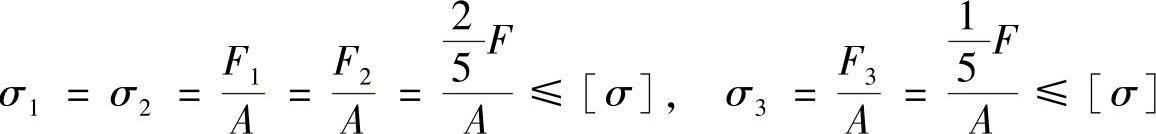
则 F≤2.5[σ]A 或 F≤5[σ]A
所以,许用载荷 [F]=2.5[σ]A
例2-11 在如图2-11a所示结构中,杆CD为刚性杆,已知F=3kN,斜杆AB的横截面积A=100mm2,许用应力[σ]=160MPa,试校核AB杆的强度。
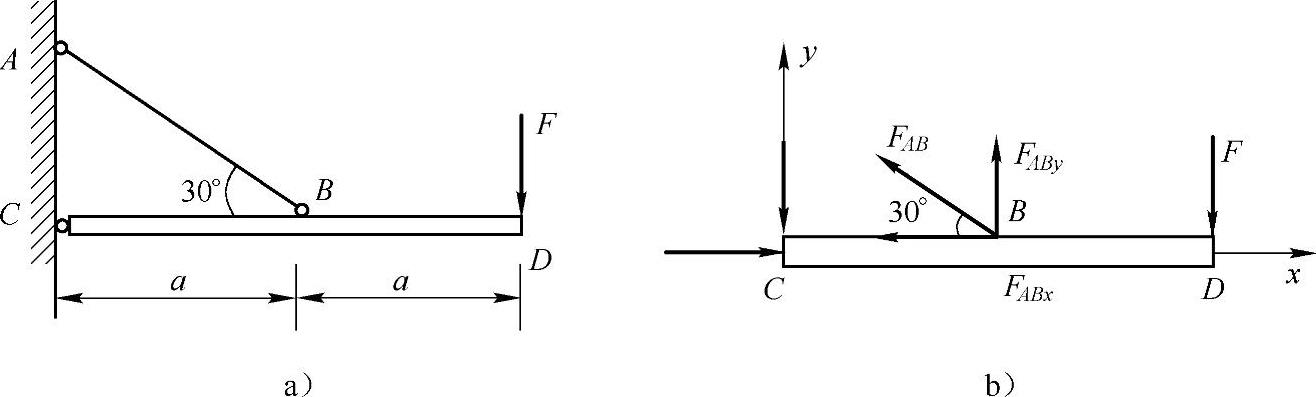
图2-11 例2-11图
解:(1)列平衡方程 取刚体CD作为研究对象,其受力如图2-11b所示,设杆AB的轴力为FAB,由
ΣMC=0,即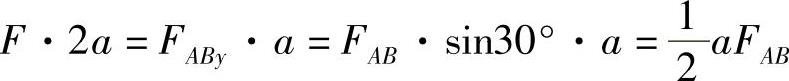
得 FAB=4F=12kN
(2)AB杆应力
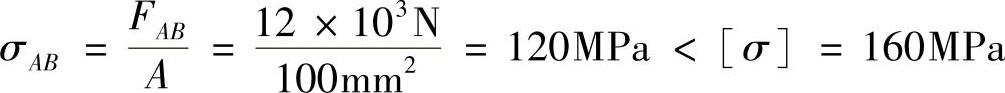
所以,杆AB是安全的。
