5.1.3  弯曲切应力计算

5.1.3 弯曲切应力计算

（1）矩形截面梁

矩形截面梁（图5-1）横截面上任意一点处的切应力计算公式为

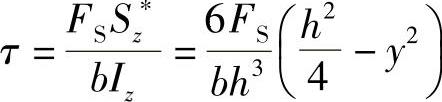
最大切应力发生在横截面的中性轴上，即y=0，且

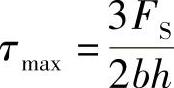
（2）工字形截面梁

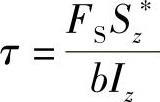
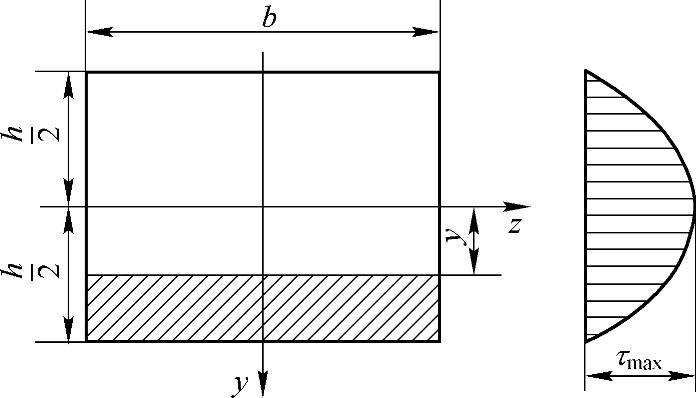
图5-1 矩形截面梁

式中，b为腹板的宽度；S_z^∗为图5-2中阴影部分的面积对中性轴的静矩。

工字形腹板上的切应力的方向也与截面上的剪力F_S一致，切应力沿腹板的高度也是按抛物线规律变化，在中性轴上切应力的数值最大。

（3）圆形截面梁

切应力分布规律：截面边缘上各点处切应力的方向与圆周相切，等高度各点处的切应力汇交于一点。

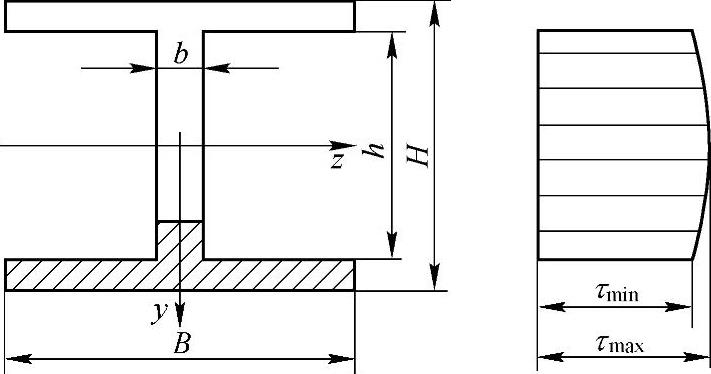
图5-2 工字形截面梁

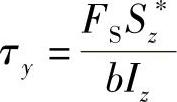
式中，b为AB弦的长度；S_z^∗为图5-3中所画阴影线的面积对z轴的静矩。在中性轴上，切应力为最大值τ_max，且各点的τ_y就是该点的总切应力，对于中性轴上的点，

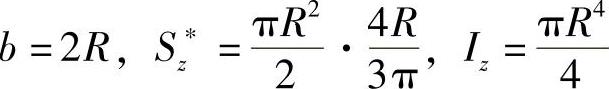
最后得到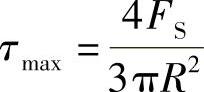

（4）梁的切应力强度计算

梁的最大切应力不得超过材料的许用切应力，即

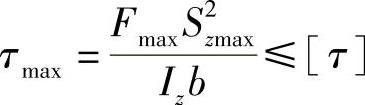
切应力的强度计算同样有强度校核、截面设计和许用载荷计算问题。