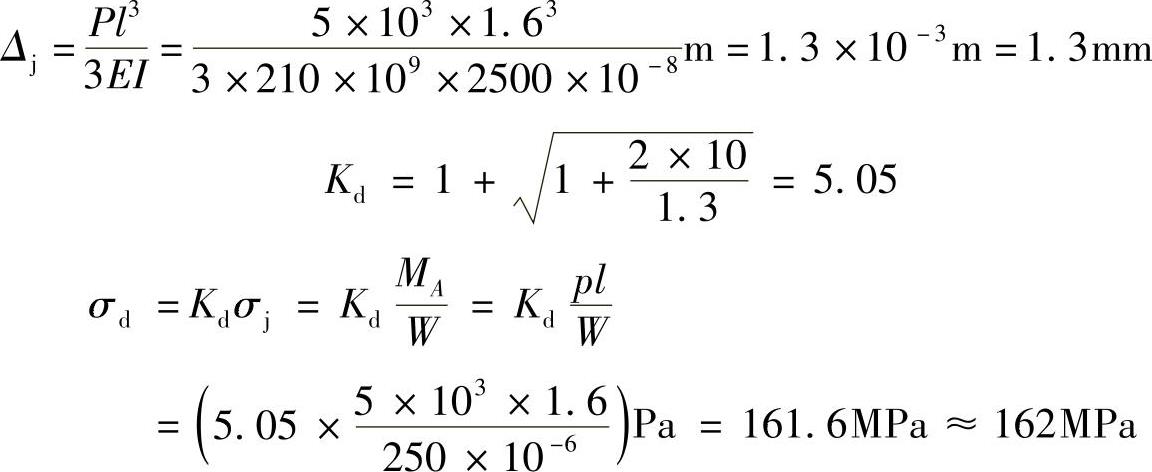10.3 例题解析
例10-1 如图10-1所示，一起重机重P1=5kN，装在两根跨度l=4m的20a工字钢梁上，用钢索起吊P2=50kN的重物。该重物在前3s内按等加速上升10m。已知[σ]=170MPa，试校核梁的强度（不计梁和钢索的自重）。
解：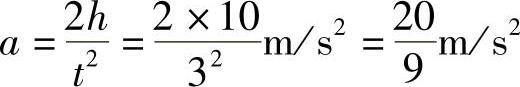
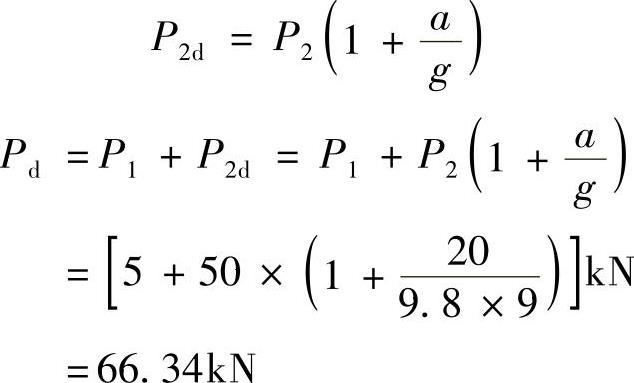
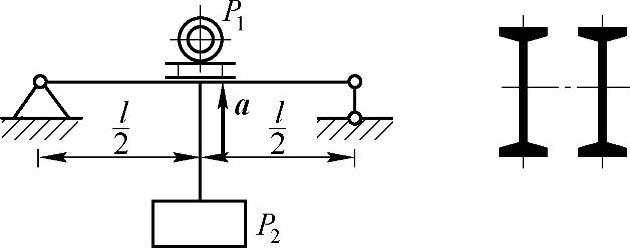
图10-1 例10-1图
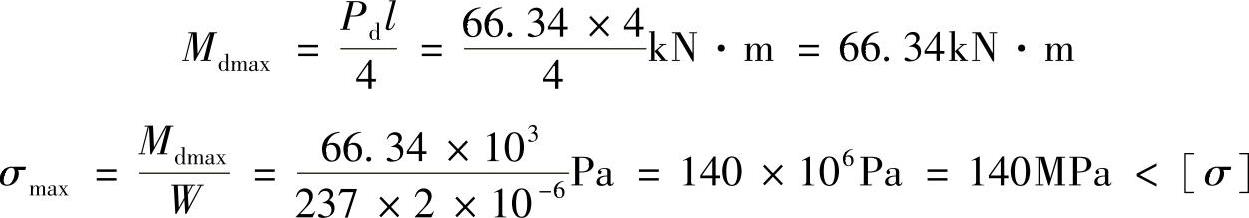
该梁符合强度要求。
例10-2 如图10-2所示，一重量为G的物体以速度v沿水平方向冲击等截面直杆AB的顶端B，杆长度为a，抗弯刚度为EI，抗弯截面系数为Wz，略去剪力的影响，试求AB杆的最大正应力。
解：此为水平冲弯，由公式可得到梁的静变形为
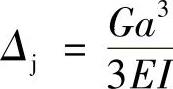
又因为
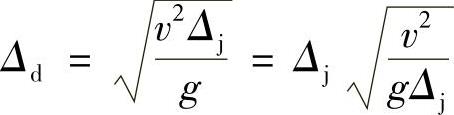
由能量守恒定理可知，拉伸、压缩应变能存在如下关系：
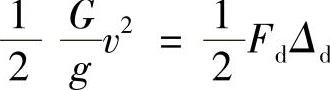
图10-2 例10-2图
因此可以求出
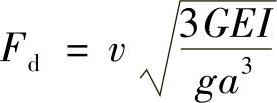
故AB杆的最大正应力在A点出现，大小为
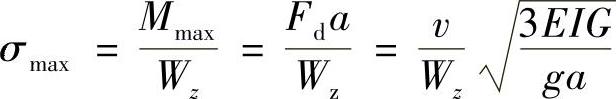
例10-3 如图10-3a所示起重机机构的重量为20kN，装在由两根32a工字钢组成的梁上，用绳索吊起重物60kN，并在第1s内以等加速上升2.5m，试求绳内所受拉力及梁的最大正应力（考虑梁的自重）。
解：这是等加速直线运动情况下的动载荷计算问题。
（1）加速度。
由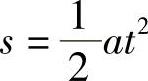
可得
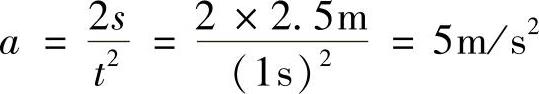
（2）动荷因数
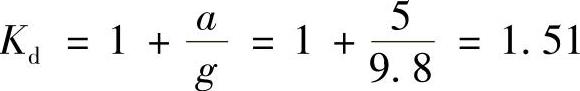
（3）绳所受拉力
Fd=KdG=1.51×60kN=9.06×104N
（4）梁的最大正应力
查型钢表得32a工字钢有
q=527N/m，Wz=692.2×10-6m3
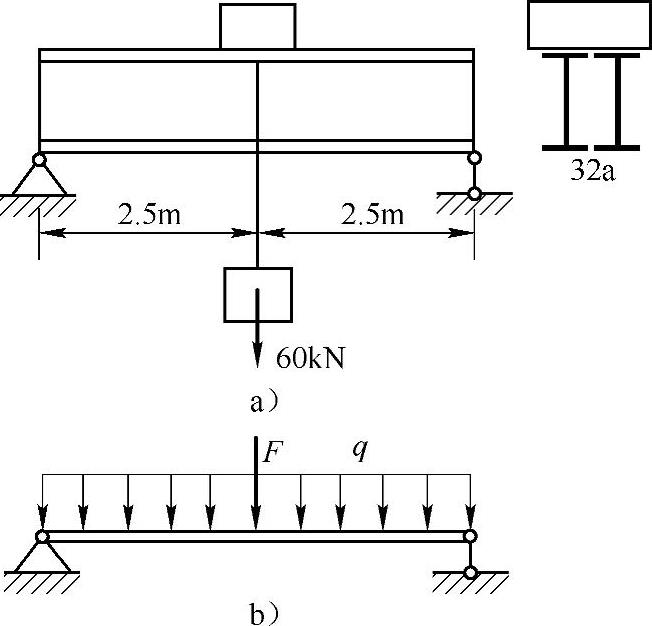
图10-3 例10-3图
梁受力如图10-3b所示，其中
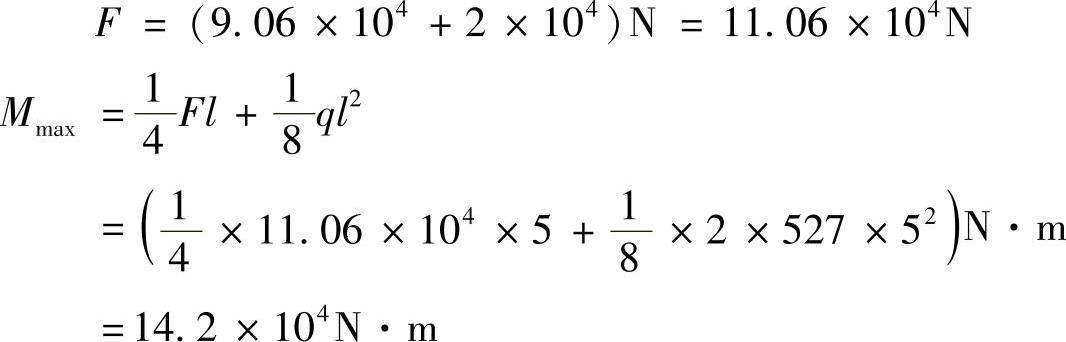
梁的最大正应力为
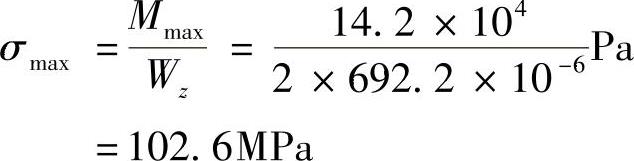
例10-4 由d=20mm的圆截面钢杆构成平均半径为R0=200mm的曲杆，如图10-4所示。有一重物W=400N，自高度H=30mm处自由落下，试求W作用点C的位移。材料的弹性模量E=200GPa。
解：（1）C点在W作用下的静位移。
因为对称，所以A和B两点的支反力满足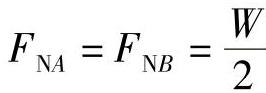
。用卡氏定理求位移，首先写出弯矩方程并求得
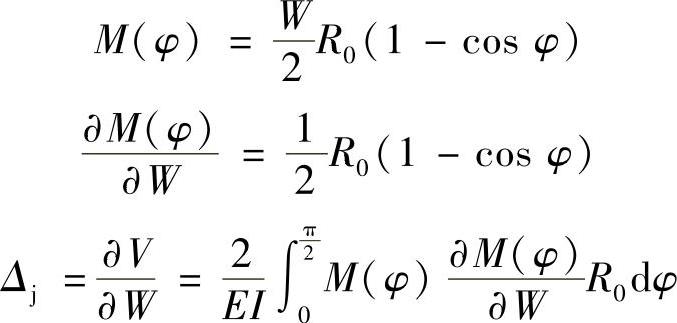
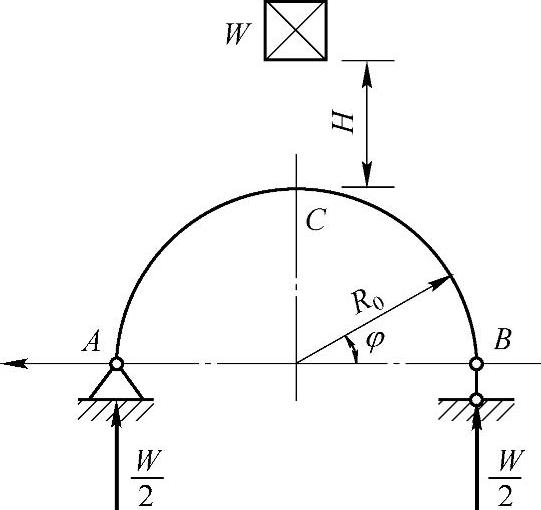
图10-4 例10-4图
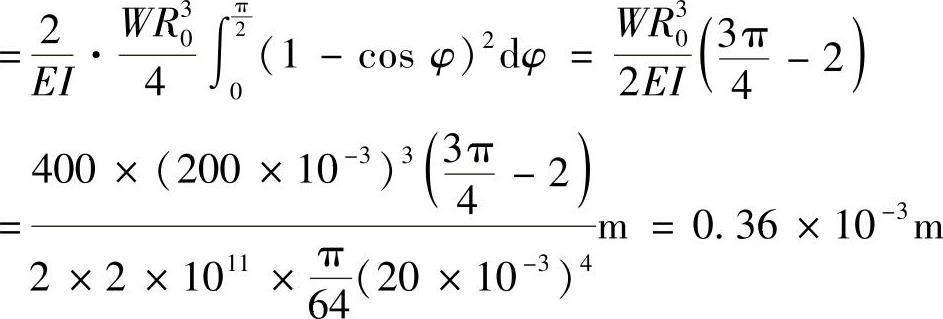
（2）动荷因数
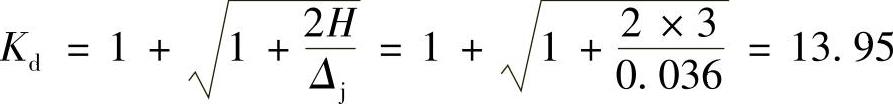
（3）动位移
ΔC=KdΔj =13.95×0.36×10-3m=5.02mm
例10-5 如图10-5所示的等截面钢架，一重量为P=300N的物体，自高度h=50mm处自由落下，试计算钢架内的最大正应力。已知材料的弹性模量E=200GPa，刚体质量与冲击物的变形均忽略不计。
解：（1）由单位载荷法计算点A的静位移
即
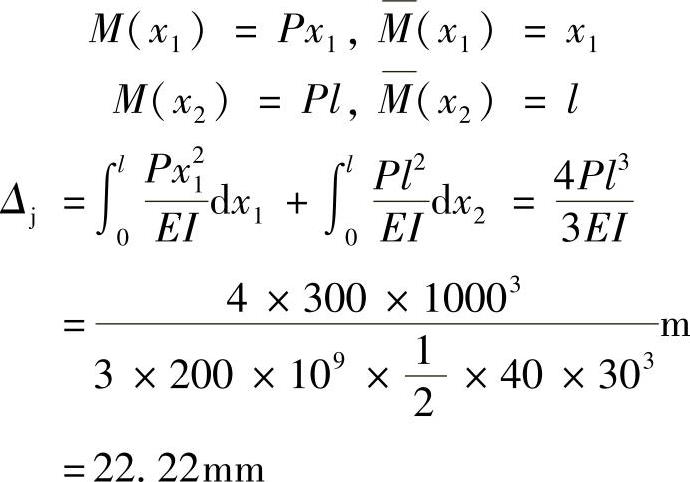
（2）最大动应力为
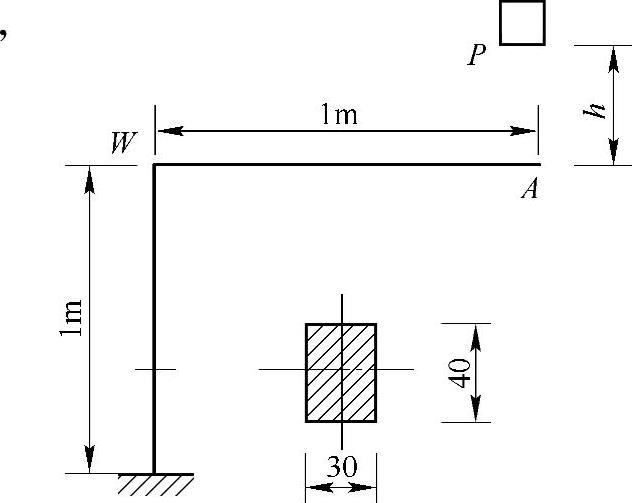
图10-5 例10-5图
例10-6 如图10-6所示，AC杆在水平平面ABC内，绕过A点的垂直轴以匀角速度ω转动，杆的C端有一重为G的集中质量，如因支座B的约束，AC杆突然被停止转动，试求AC杆内最大冲击应力（忽略杆AC的质量）。
解：这是水平冲击问题，由题意知，杆AC在水平平面内转动，因此冲击物的势能不变，只有动能和应变能的变换，根据能量守恒有T=Vd。冲击开始的瞬时，重物G在C点有速度ωl，冲击结束时，其末速度为零，故动能增加为
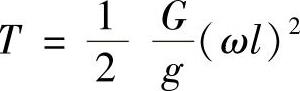
杆应变能Vd的变化就等于冲击力Fd在位移Δd上所做的功，即
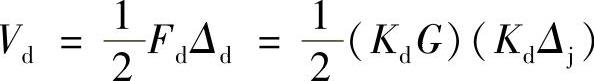
于是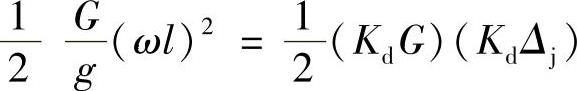 
由此可得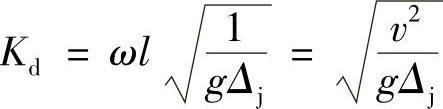 
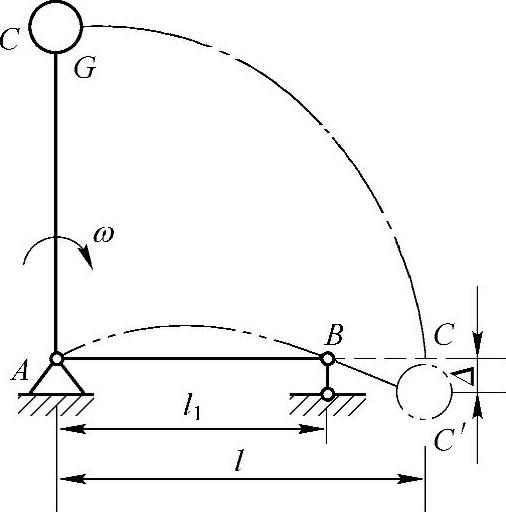
图10-6 例10-6图
以G作为静载荷作用于C点，引起AC杆在C点的静挠度为
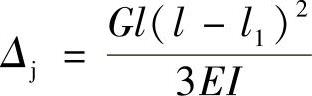
所以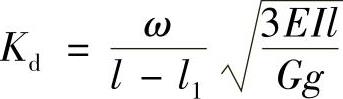 
AB杆B截面上具有最大的弯矩为
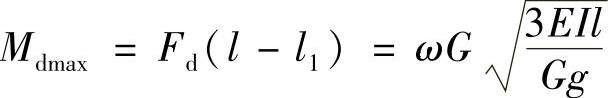
所以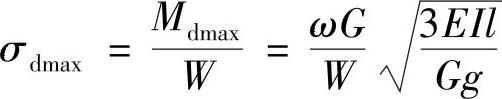 
例10-7 在直径d=100mm的轴上，装有转动惯量I0=0.5kN·m·s2的飞轮，轴以300r/min的匀角速度旋转，如图10-7所示。现用制动器使飞轮在4s内停止转动，试求轴内的最大切应力（不计轴的质量和轴承内的摩擦）。
解：设轴为等减速转动，其角加速度为
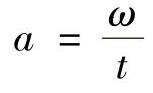
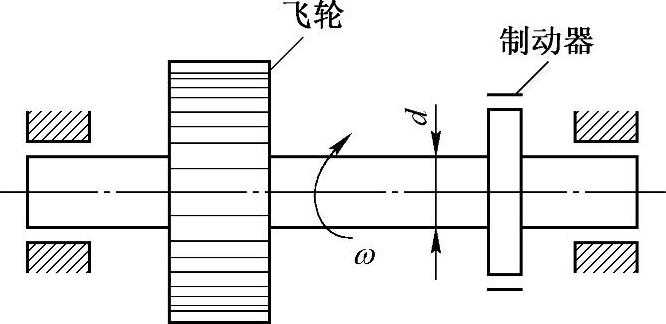
图10-7 例10-7图
由Td=I0a得
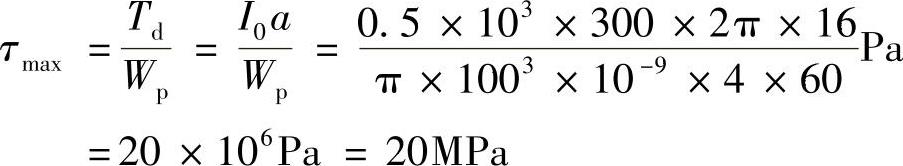
例10-8 重量为P=5kN的重物自高度h=10mm处自由下落，冲击到20b工字钢梁上的B点处，如图10-8所示。已知钢的弹性模量E=210GPa。试求梁内最大冲击正应力（不计梁的自重）。
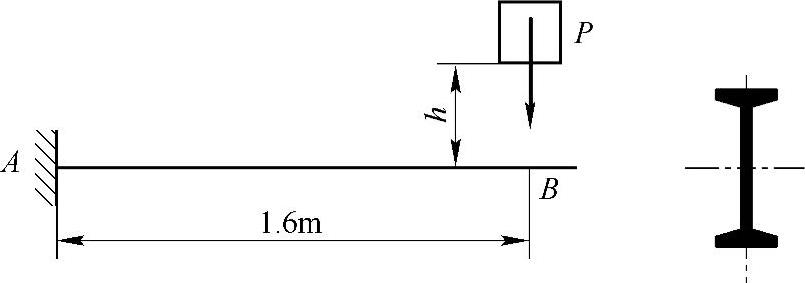
图10-8 例10-8图
解：