7.1.2  平面应力状态分析

7.1.2 平面应力状态分析

（1）解析法

1）图7-1所示垂直于xy平面的任意斜截面ef以它的外法线n与x轴的夹角α定义，且α角以自x轴逆时针转至外法线n为正；斜截面上图中所示的正应力σ_α和切应力τ_α均为正值，即σ_α以拉应力为正，τ_α以使其所作用的体元有顺时针转动趋势者为正。

2）与z平面垂直的任意斜截面上的应力为

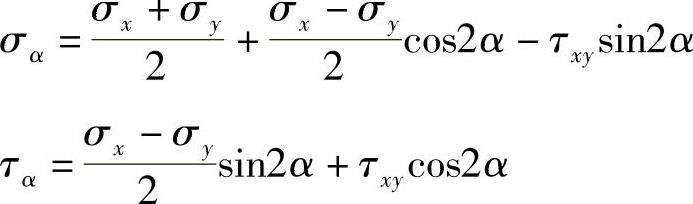
3）最大正应力和最小正应力为

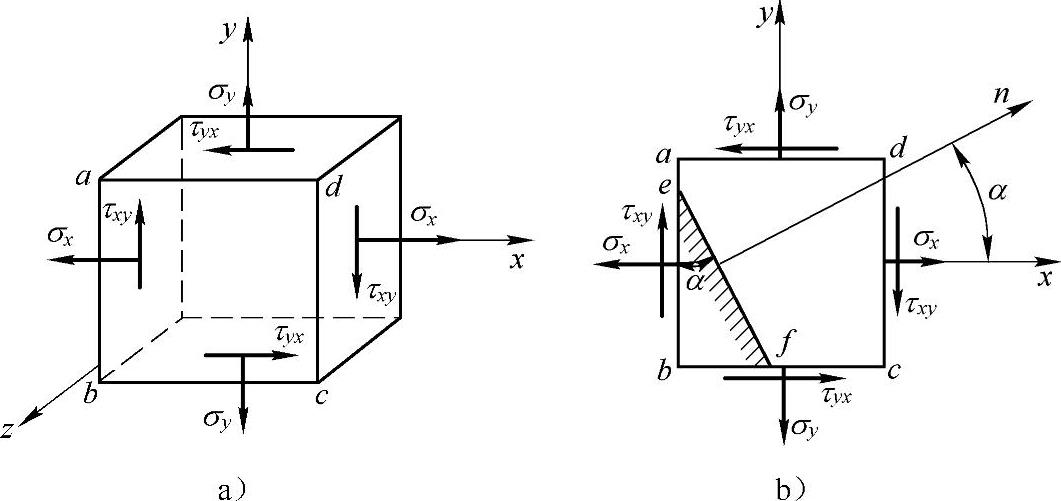
图 7-1

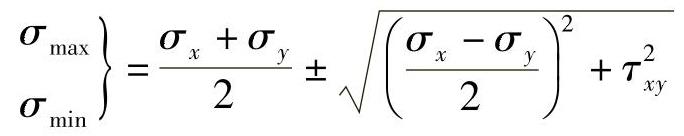
最大正应力和最小正应力是平面应力状态的两个主应力，位于与x轴成α₀，α₀+90°倾角的两个主平面上，由此得出

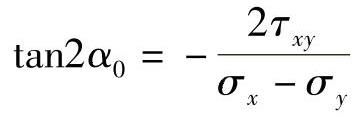
4）最大切应力和最小切应力 主切应力即切应力极值。两个主切应力大小相等，方向相反，即遵守切应力互等定理，并且大小等于两个主应力之差的一半，即

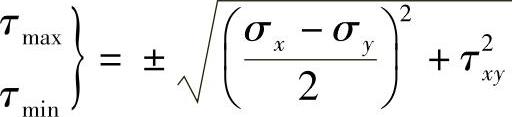
最大切应力和最小切应力所在截面相互垂直，位于α₁，α₁+90°的平面，且

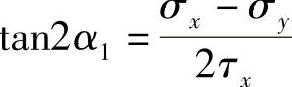
其作用面与主平面成±45°。

（2）图解法（应力圆法）

1）平面应力状态下，为了求得σ_α，τ_α，便于直观地了解平面应力状态的一些特征，可使上述σ_α和τ_α的计算公式以图形即应力圆（莫尔圆）来表示。在σ，τ的直角坐标系中，应力圆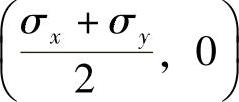以为圆心，以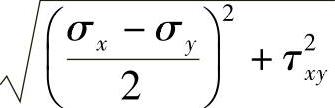为半径，如图7-2所示。

2）作应力圆步骤。将单元体x截面上的应力σ_x，τ_x按某一比例尺定出点D₁，依单元体y截面上的应力σ_y，τ_yx（取τ_xy=-τ_yx）定出点D₂，然后连一直线，以它与σ轴的交点C为圆心，并且以CD₁或CD₂为半径作圆得出。

3）利用应力圆求α斜截面（图7-2a）上的应力σ_α，τ_α时，只需将应力圆圆周上表示x截面上的应力的点D₁所对应的半径CD₁按方位角α的转向转动2α角，得到半径CE，那么圆周上E点的坐标便代表了单元体α斜截面上的应力。

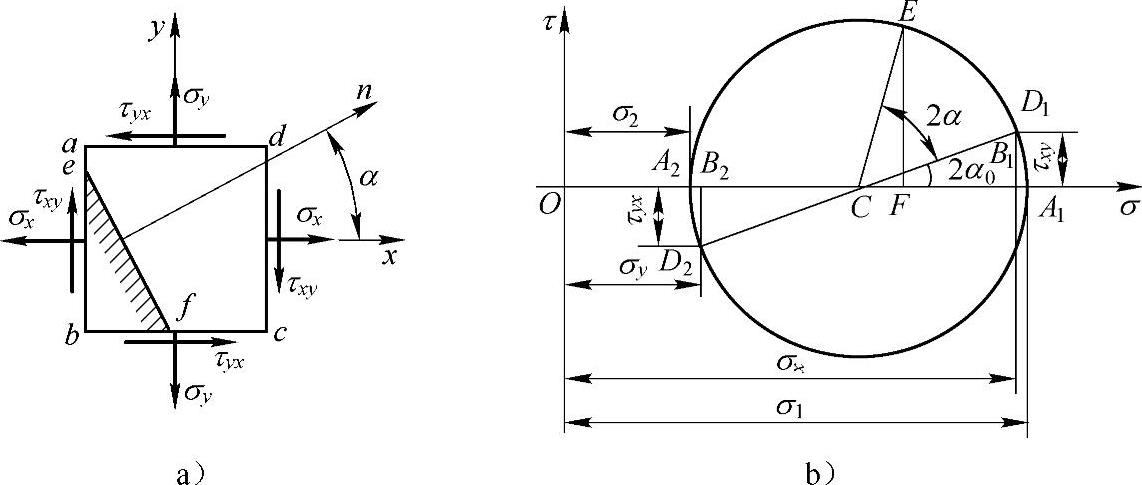
图 7-2

4）在应力圆圆周上代表单元体两个相互垂直的x截面和y截面上应力的点D₁和D₂所夹圆心角为180°，它是单元体上相应两个面之间夹角的两倍，这反映了前述σ_α和τ_α计算公式中以2α为参变量。