9.1.3  压杆的临界应力

9.1.3 压杆的临界应力

（1）临界应力与柔度

将临界载荷F_cr除以压杆的横截面面积A，即可求得压杆的临界应力，即

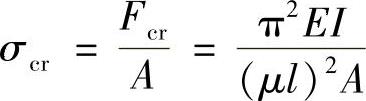
将截面对中性轴的惯性半径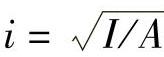代入得临界应力欧拉公式为

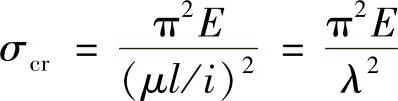
式中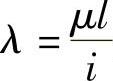，为柔度或长细比。它是一个无量纲量。λ值越大，压杆就越容易失稳。

（2）欧拉公式的适用范围

若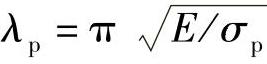，欧拉公式的适用范围可用柔度表示为

λ≥λ_p

其中，λ≥λ_p的压杆称为大柔度杆或细长杆，其临界力或临界应力可用欧拉公式来计算。

（3）超出比例极限时压杆的临界应力

当压杆的柔度值λ＜λ_p时，说明压杆横截面上的应力已超过了材料的比例极限σ_p，这时欧拉公式已不再适用。在这种情况下，压杆的临界应力在工程计算中常采用建立在实验基础上的经验公式来计算，其中有在机械工程中常用的直线经验公式和在钢结构中常用的抛物线经验公式。

1）经验公式 常用的直线经验公式为

σ_cr=a-bλ

式中，a，b是与材料的力学性能有关的两个常数，可以通过试验加以测定，使用时可从有关手册上查取。

2）临界应力总图 如果将临界应力与柔度之间的函数关系绘在σ_cr-λ直角坐标系内，将得到临界应力随柔度变化的曲线图形，称为临界应力总图。如图9-1所示。

临界应力均随柔度λ的增大而呈逐渐衰减的变化规律。也就是说，压杆越细越长，就越容易失去稳定。但对于柔度较小的短粗杆，其临界应力σ_cr接近材料的屈服极限σ_s，曲线的曲率比较平缓，一般可取σ_s或σ_b作为临界应力。这说明短粗杆的破坏不是失稳而是强度破坏了。

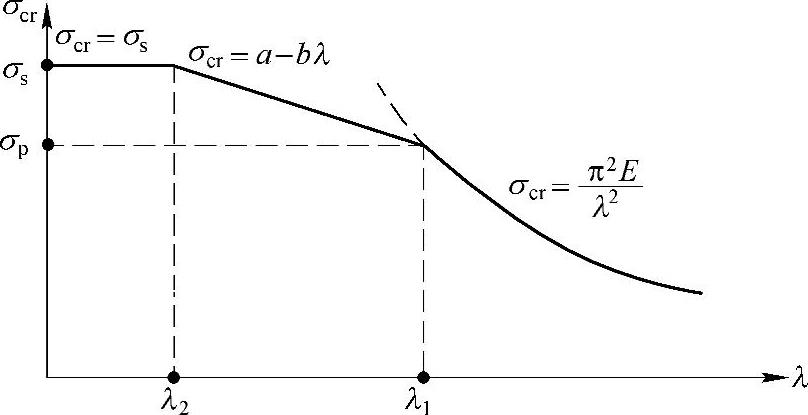
图 9-1