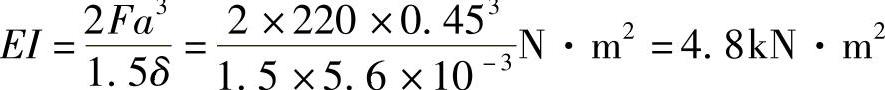6.3  例题解析

6.3 例题解析

例6-1 图6-2所示简支梁AB受集中力F作用，试求该梁的最大挠度和转角。

解：（1）求反力并列梁的弯矩方程。

简支梁AB的支反力为

，

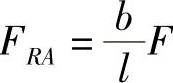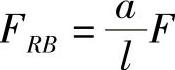
按图6-2所示坐标系Axy，分两段列出AB梁的弯矩方程为

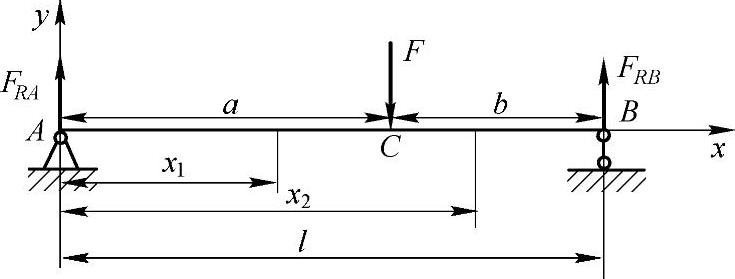
图6-2 例6-1图

AC段：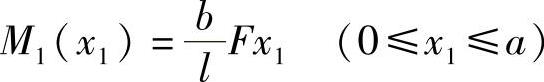

CB段：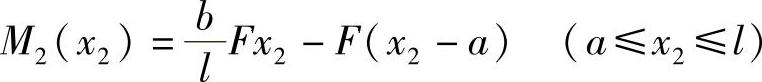

（2）列出梁的各段的挠曲线近似微分方程并积分。

将AC和CB两段的挠曲线近似微分方程及积分结果，列于表6-1。

在CB梁段，对含有（x₂-a）的项积分时，就以（x₂-a）作为自变量进行积分，这样可以使确定积分常数的计算得到简化。

（3）确定积分常数。

积分出现的四个积分常数C₁，D₁和C₂，D₂，需要四个条件来确定。由于AB梁的挠曲线应该是一条光滑连续的曲线，因此，在AC和CB两段挠曲线的交界截面C处，挠曲线应有唯一的挠度和转角。即挠曲线在C截面的连续条件为

当x₁=x₂=a时，θ₁=θ₂，w₁=w₂

即

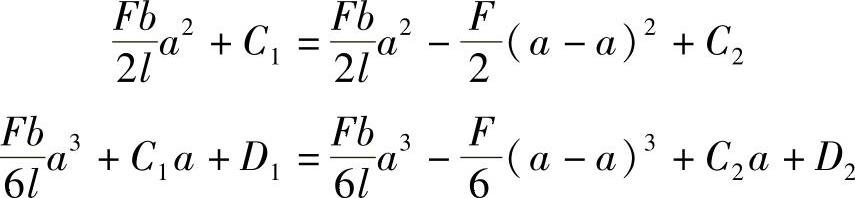
由以上两式解得C₁=C₂，D₁=D₂

此外，梁在A，B两端的边界条件为

x₁=0时， w₁=0

x₂=l时， w₂=0

即

D₁=0

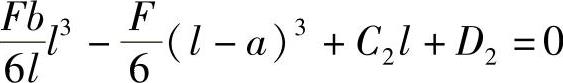
解得

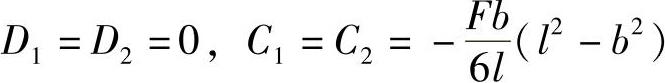
将梁AC和CB段的转角方程和挠曲线方程列于表6-2中。

表 6-1

表 6-2

（4）求梁的最大挠度和转角。

在梁的左端截面的转角为

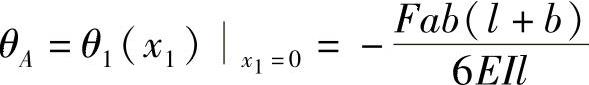
在梁右端截面的转角为

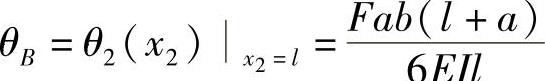
当a＞b时，可以断定θ_B为最大转角。

为了确定挠度为极值的截面，先确定C截面的转角，则

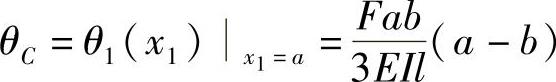
若a＞b，则转角θ_C＞0。AC段挠曲线为光滑连续曲线，而θ_A＜0，当转角从截面A到截面C连续地由负值变为正值时，AC段内必有一截面转角为零。为此，令x₁=x₀时的θ₁（x₁）=0，即

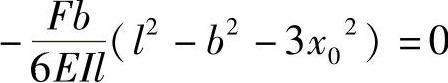
解得

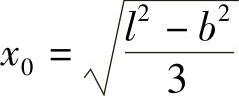
x₀的转角为零，亦即挠度最大的截面位置。由AC段的挠曲线方程可求得AB梁的最大挠度为

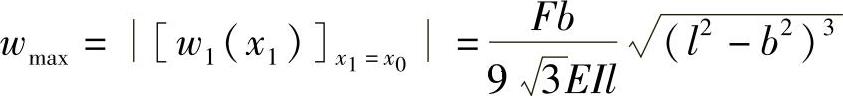
例6-2 试用叠加法求图6-3所示梁指定截面的挠度和转角。设梁的抗弯刚度EI为已知。

解：（1）当F单独作用时，查表得

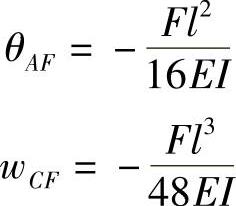
（2）当M_e单独作用时，查表得

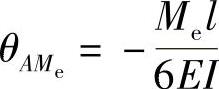
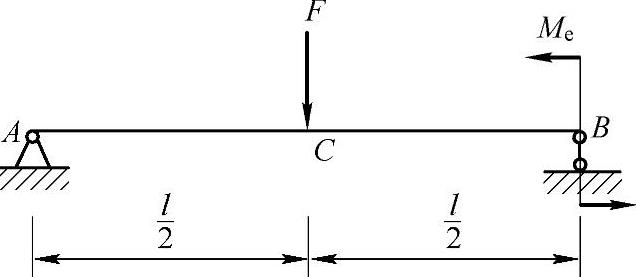
图6-3 例6-2图

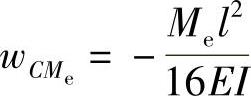
（3）当F和M_e共同作用时，则

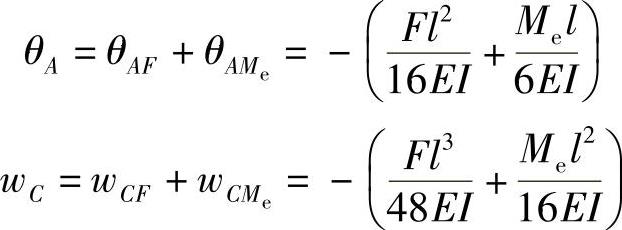
例6-3 已知一钢轴的飞轮A重F=20kN，轴承B处的许可转角[θ_B]=0.5°，钢的弹性模量E=200GPa。试确定轴的直径d。

轴的受力简图：

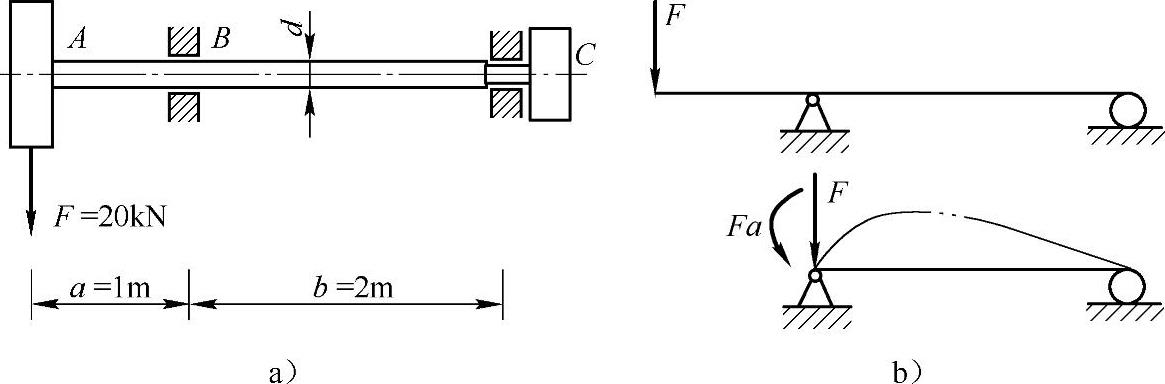
图6-4 例6-3图

解：（1）作轴的受力简图，如图6-4b所示。

（2）由刚度条件确定轴的直径。

由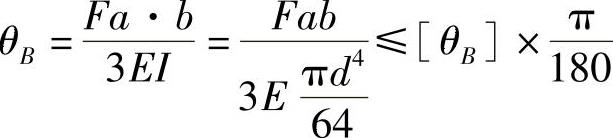

可得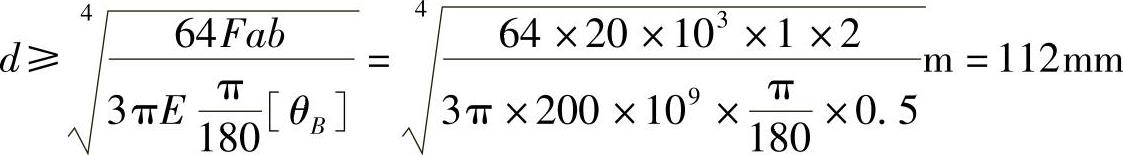

例6-4 若弹簧的平均半径R=80mm，簧丝直径d=20mm，圈数n=7，材料的切变模量G=80GPa。在图6-5所示载荷作用下，若CDE梁的端点E的位移等于弹簧伸长量的1.5倍，试求CDE梁的抗弯刚度EI。

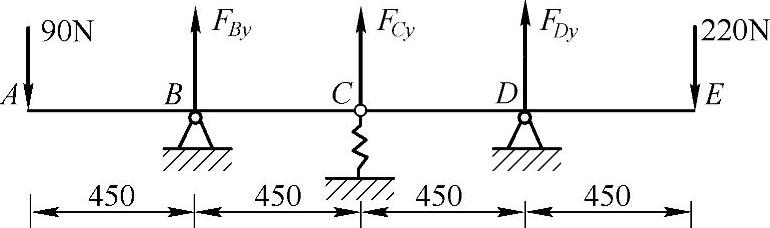
图6-5 例6-4图

解：（1）求支反力。

考虑ABC梁段的平衡可得 F_By=180N

考虑CDE梁段的平衡可得 F_Dy=440N

考虑整个梁的平衡可得 F_Cy=310N

（2）求弹簧的伸长量。

弹簧所受到的力为

F=F_Cy=310N

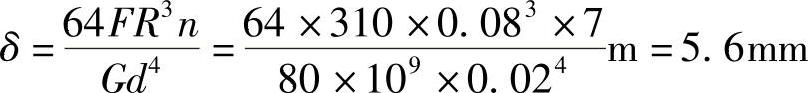
（3）求E点的位移。

考虑CDE梁段（记F=220N，a=450mm）

1）先将C点看做固定铰支座，由叠加法

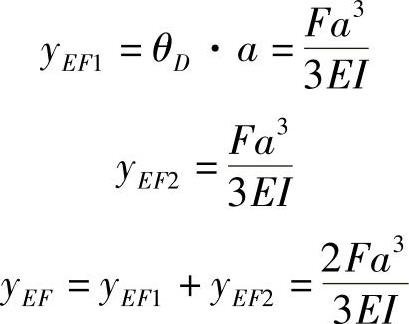
2）由弹簧伸长引起的E点位移

y_Eδ=δ

3）E点的总位移

（4）求CDE梁段的抗弯刚度。

根据题意 y_E=1.5δ （2）

由式（1）、式（2）求得