附录A 应用控制截面法画杆件内力图小结
当构件的受载与变形情况不同时,其内力就不同,绘出的内力图也就不同。轴力图、扭矩图、剪力图和弯矩图都是不同的内力图。本章介绍应用控制截面法绘制内力图。
A.1 概述
控制截面的概念:外力规律发生变化的截面——集中力、集中力偶作用点、分布载荷的起点和终点处的横截面,如图A-1所示。某一截面上的内力与作用在该截面一侧局部杆件上的外力相平衡;在载荷无突变的一段杆的各截面上内力按相同的规律变化;杆件各截面上内力变化规律随着外力的变化而改变。
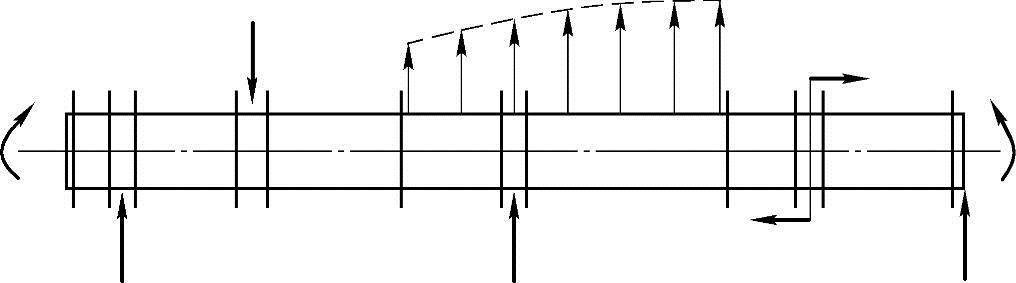
图 A-1
A.2 轴力图
A.2.1 举例
例A-1 如图A-2a所示直杆,A端固定,在B,C两处作用有集中载荷F1和F2,其中F1=5kN,F2=10kN。试画杆件的轴力图。
解:(1)确定A处的约束力。
由于杆件只有轴向载荷作用,所以固定端A处只有一个轴向的约束力FA,如图A-2b所示。
由平衡方程ΣFx=0求得 FA=5kN
(2)确定控制截面。
在集中载荷F2、约束力FA作用处的A,C截面,以及集中载荷F1作用点B处的上、下两侧横截面都是控制截面,如图A-2c所示。
(3)应用截面法求控制截面上的轴力。
用假想截面分别从控制截面A,B′,B″,C处将杆截开,假设横截面上的轴力均为正方向(拉力),并考察截开后下面部分的平衡,求得各截面上的轴力。
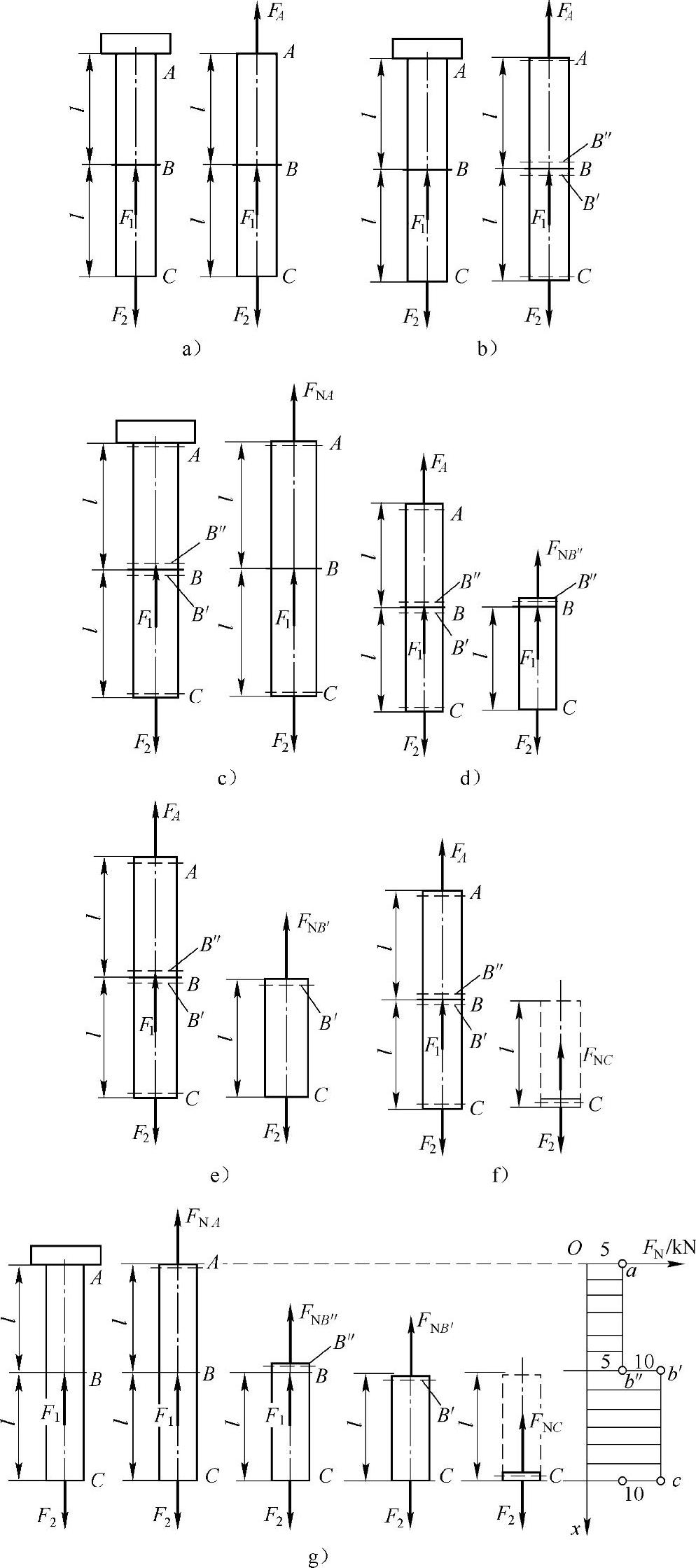
图A-2 例A-1图
由图A-2c中ΣFx=0得 FNA=F2-F1=5kN
由图A-2d中ΣFx=0得 FNB″=F2-F1=5kN
由图A-2e中ΣFx=0得 FNB′=F2=10kN
由图A-2f中ΣFx=0得 FNC=F2=10kN
(4)建立FN-x坐标系,画轴力图。
FN-x坐标系中x坐标轴沿着杆件的轴线方向,FN坐标轴垂直于x轴。
将所求得的各控制截面上的轴力标在FN-x坐标系中,得到a,b″,b′和c四点。因为在A,B之间以及B,C之间没有其他外力作用,故这两段中的轴力分别与A截面、C截面上的轴力相同。这表明a点与b″点之间以及b′点与c点之间的轴力图为平行于x轴的直线。于是,得到杆的轴力图如图A-2g所示。
A.2.2 小结
根据以上例题分析,应用控制截面法绘制轴力图的步骤归纳如下:
1)确定约束力。
2)根据杆件上作用的载荷以及约束力确定控制截面,也就是轴力图的分段点。
3)应用截面法,用假想截面从控制截面处将杆件截开,在截开的截面上画出未知轴力,并假设为正方向;对截开的部分杆件建立平衡方程,确定控制截面上的轴力。
4)建立FN-x坐标系,将所求得的轴力值标在坐标系中,画出轴力图。
A.3 扭矩图
A.3.1 举例
一传动轴如图A-3a所示,其转速n=300r/min,主动轮A输入的功率为P1=500kW。若不计轴承摩擦所耗的功率,三个从动轮输出的功率分别为P2=150kW,P3=150kW,P4=200kW。
试作扭矩图。
解:(1)计算外力偶矩。
由 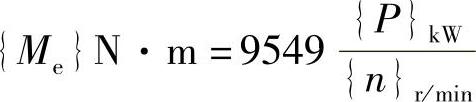
得 Me1=15915N·m,Me2=Me3=4774.5N·m,Me4=6366N·m
(2)确定控制截面。
在集中载荷力偶Me2,Me4作用处的a,f截面,以及集中载荷力偶Me3,Me1作用点处的左右两侧横截面都是控制截面,如图A-3b所示。
(3)应用截面法求控制截面上的扭矩。
计算CA段内c截面上的扭矩,假设Tc为正值,如图A-3c所示。
由ΣMx=0得
Me2+Me3+Tc=0
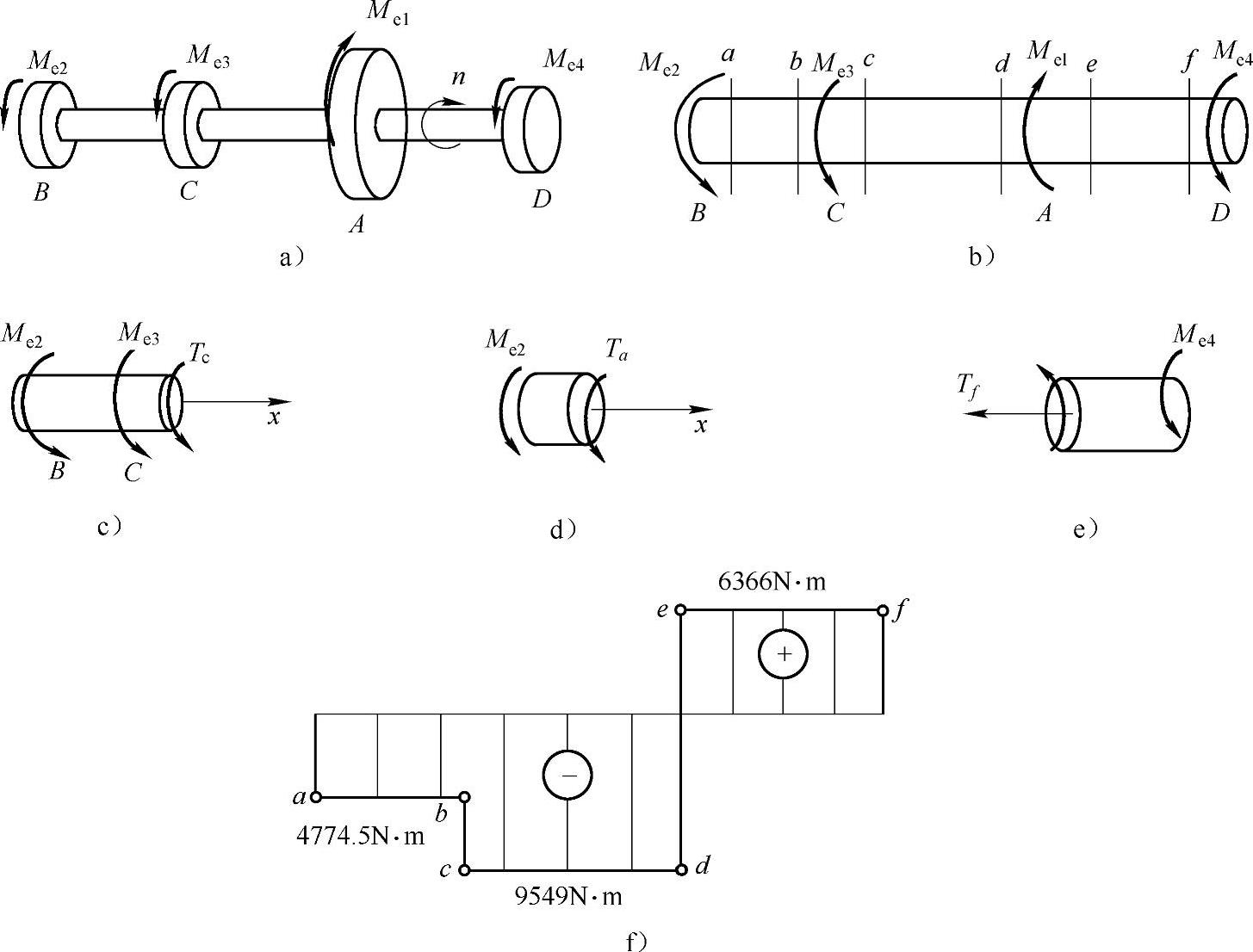
图A-3 例A-2图
则
Tc=-(Me2+Me3)=-9549N·m
同理可得
Td=-9549N·m
计算BC段内a截面上的扭矩。如图A-3d所示,由ΣMx=0得
Ta=-Me2=-4774.5N·m
同理可得
Tb=-Me2=-4774.5N·m
在AD段内,如图A-3e所示,由ΣMx=0得
Tf=Me4=6366N·m
同理可得
Te=Me4=6366N·m
(4)建立T-x坐标系,画扭矩图。
将所求得的各控制截面上的扭矩标在T-x坐标系中,得到a,b,c,d,e和f六点。因为在a,b之间,c,d之间以及e,f之间没有其他外力作用,故这三段中的扭矩分别与a,c,e截面上的扭矩相同。这表明a,b之间,c,d之间以及e,f之间的扭矩为平行于x轴的直线。于是,得到轴的扭矩图如图A-3f所示。
A.3.2 小结
根据以上例题分析,应用控制截面法绘制扭矩图的步骤归纳如下:
1)计算外力偶矩。
2)确定控制截面。
3)应用截面法,用假想截面从控制截面处将杆件截开,在截开的截面上画出扭矩,并假设为正方向;对截开的部分杆件建立平衡方程,确定控制截面上的扭矩。
4)建立T-x坐标系,将所求得的扭矩值标在坐标系中,画出扭矩图。
A.4 剪力图、弯矩图
A.4.1 举例
例A-3 简支梁受力的大小和方向如图A-4所示。
解:(1)确定约束力。
根据力矩平衡方程
ΣMA=0, ΣMB=0
求得A,B两处的约束力分别为
FAy=0.89kN,FBy=1.11kN
(2)确定控制截面。
在集中力和集中力偶作用处的两侧截面以及支座约束力内侧截面均为控制截面。即A,C,D,E,F,B截面,如图A-4b所示。
(3)建立坐标系。
建立FS-x和M-x坐标系。
(4)确定控制截面上的剪力和弯矩值。
应用截面法确定控制截面上的剪力和弯矩值,并将其标在FS-x和M-x坐标系中。
(5)根据微分关系连线。
因为梁上无分布载荷作用,所以剪力FS图形均为平行于x轴的直线;弯矩M图形均为斜直线。于是,顺序连接FS-x和M-x坐标系中的a,b,c,d,e,f各点,便得到梁的剪力图与弯矩图。
A.4.2 小结
根据以上例题分析,应用控制截面法绘制剪力图、弯矩图的步骤归纳如下:
1)根据载荷及约束力的作用位置,确定控制截面。
2)应用截面法确定控制截面上的剪力和弯矩数值。
3)建立FS-x和M-x坐标系,并将控制截面上的剪力和弯矩值标在相应的坐标系中。
4)应用平衡微分方程确定各段控制截面之间的剪力图和弯矩图的形状,进而画出剪力图与弯矩图。
A.5 刚架的内力图
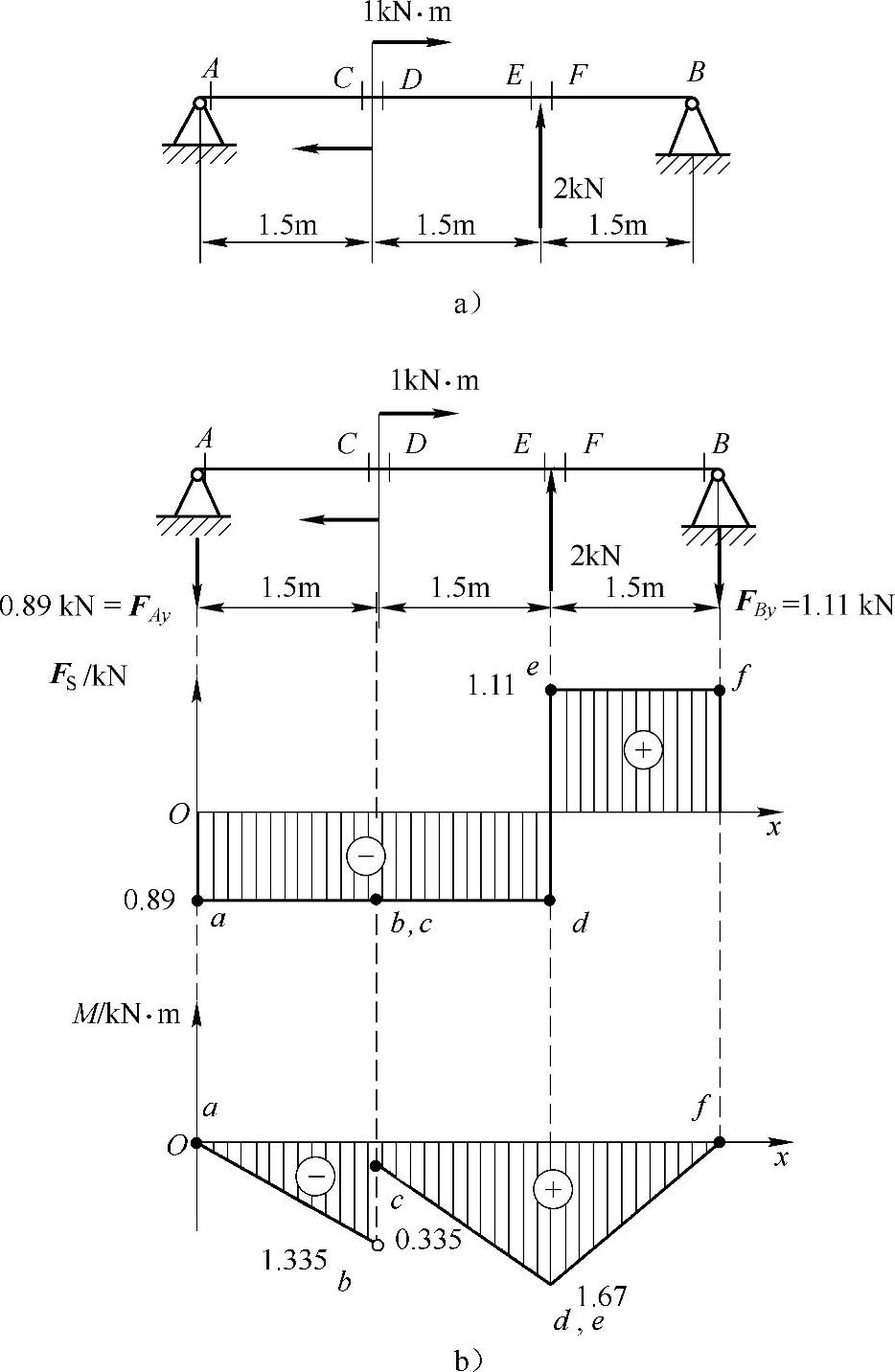
图A-4 例A-3图
A.5.1 举例
例A-4 已知平面刚架上的均布载荷集度q,长度l,如图A-5a所示。画出刚架的内力图。
解:(1)确定约束力,如图A-5b所示。
(2)确定控制截面,如图A-5c所示分别为A,B′,B″,C。
(3)确定控制截面上的内力。
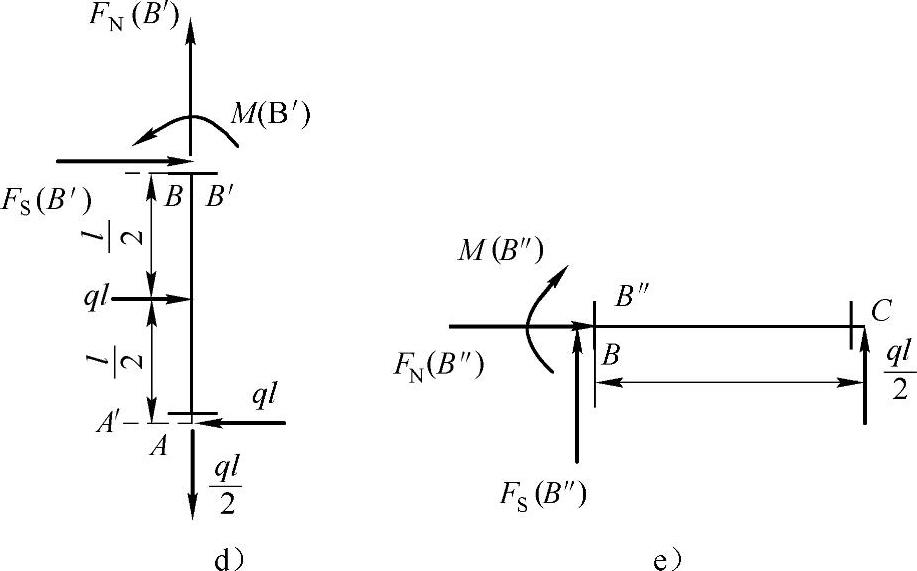
沿B截面截开,考虑AB杆平衡,受力如图A-5d所示。
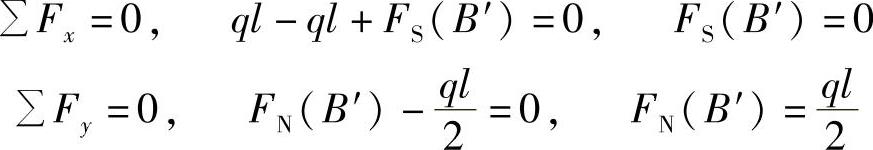
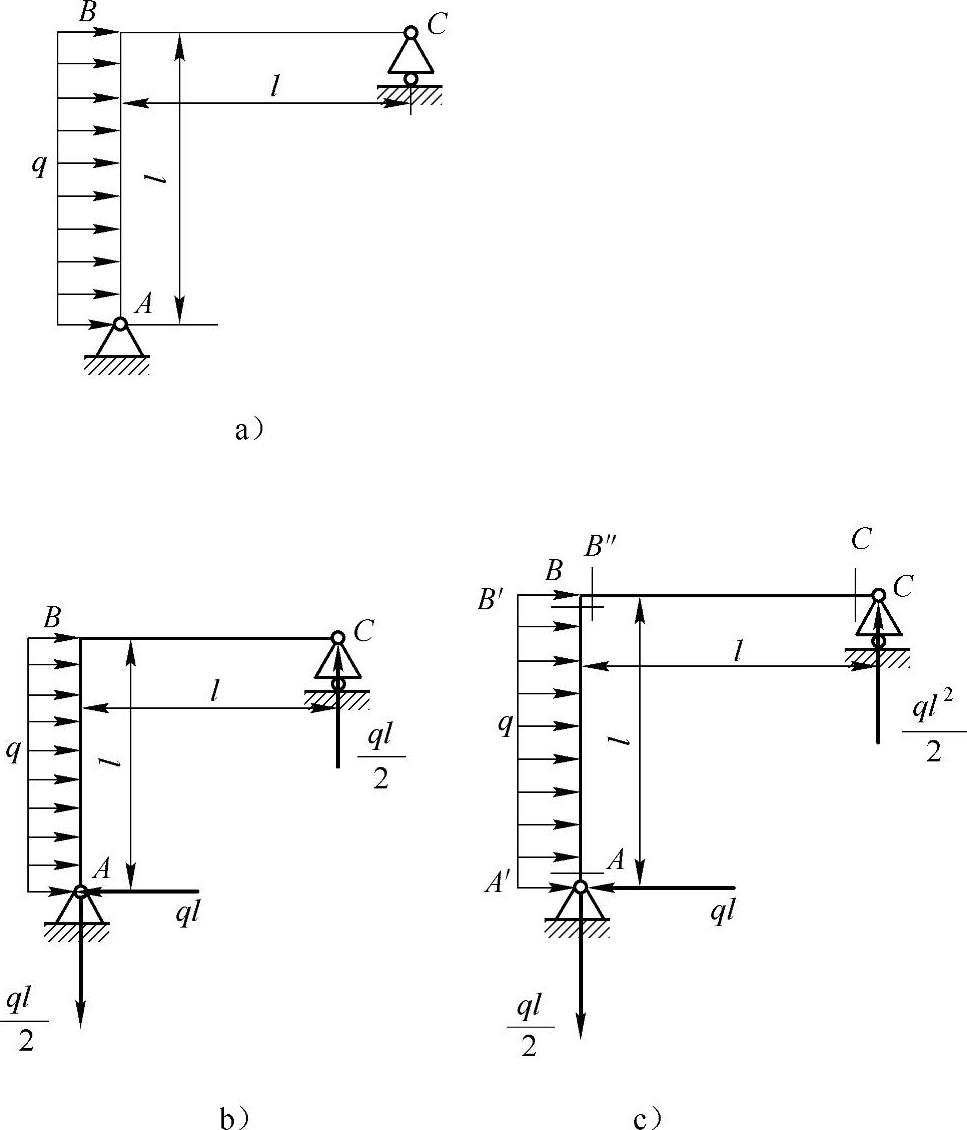
图A-5 例A-4图
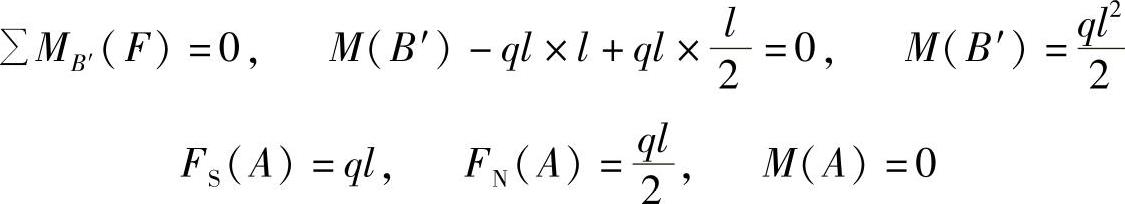
沿B截面截开,考虑BC杆平衡,受力如图A-5e所示。
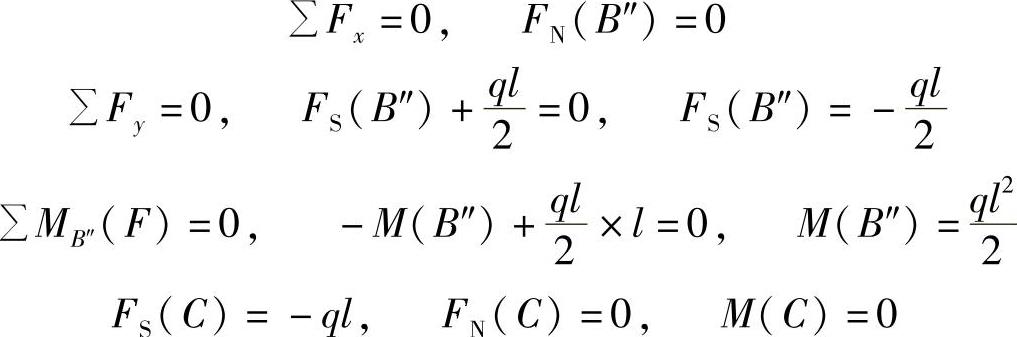
(4)画剪力图和弯矩图。
将控制截面上的剪力和弯矩分别标在FS和M坐标中,根据微分关系连线。剪力图标上正负号,弯矩图画在受压的一侧,如图A-5f、g所示。
(5)画轴力图。
将控制截面上的轴力标在FN坐标中并连线,根据轴力的拉、压性质,在图A-5h上标上正负号。
A.5.2 小结
根据以上例题分析,应用控制截面法绘制刚架内力图的步骤归纳如下:
1)根据载荷及约束力的作用位置,确定控制截面。
图A-5 例A-4图(续)
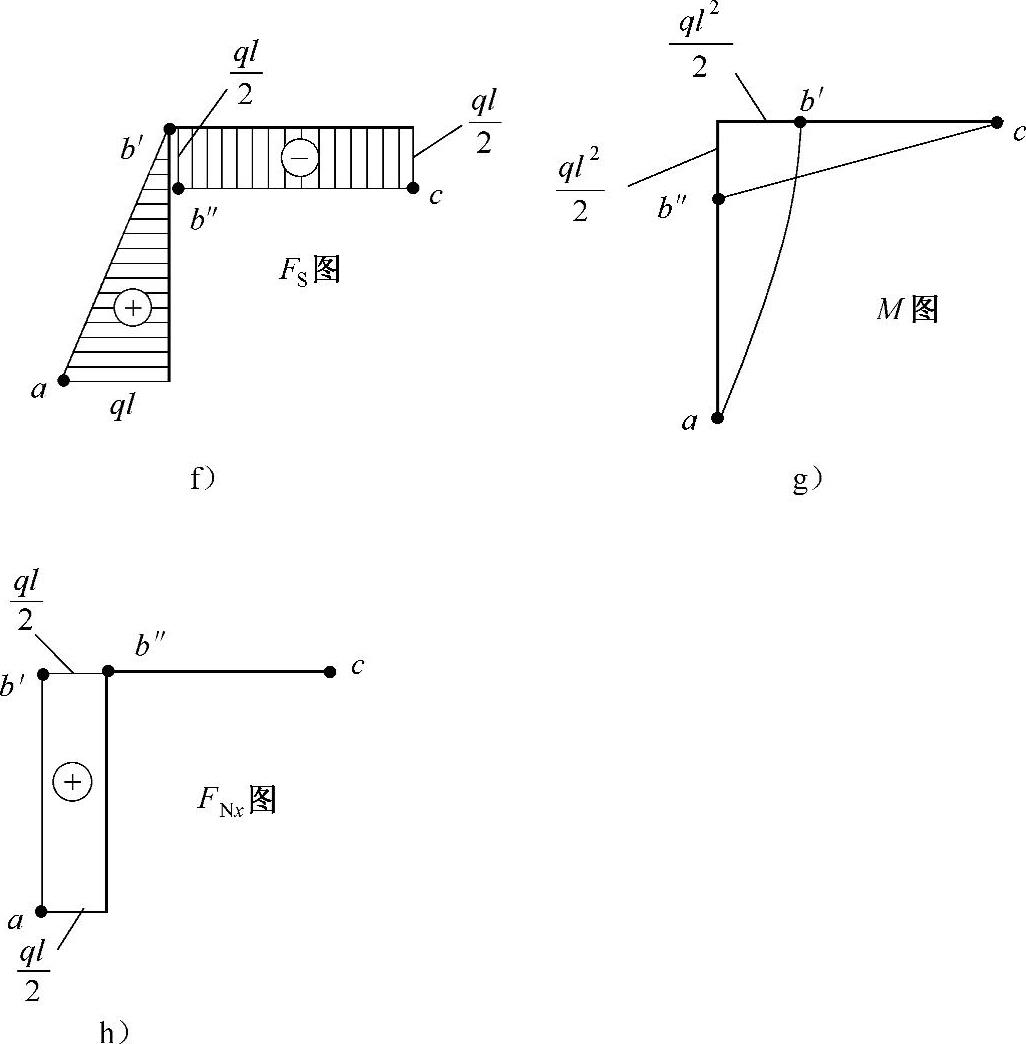
图A-5 例A-4图(续)
2)应用截面法确定控制截面上的轴力、剪力和弯矩数值。
3)建立FS-x、M-x和FN-x坐标系,并将控制截面上的轴力、剪力和弯矩值标在相应的坐标系中。
4)将所求得的轴力值标在坐标系中,画出轴力图。应用平衡微分方程确定各段控制截面之间的剪力图和弯矩图的形状,进而画出剪力图与弯矩图。
