4.3 例题解析
例4-1 写出如图4-1a所示梁的剪力方程和弯矩方程,并作梁的剪力图和弯矩图,求最大剪力和最大弯矩。
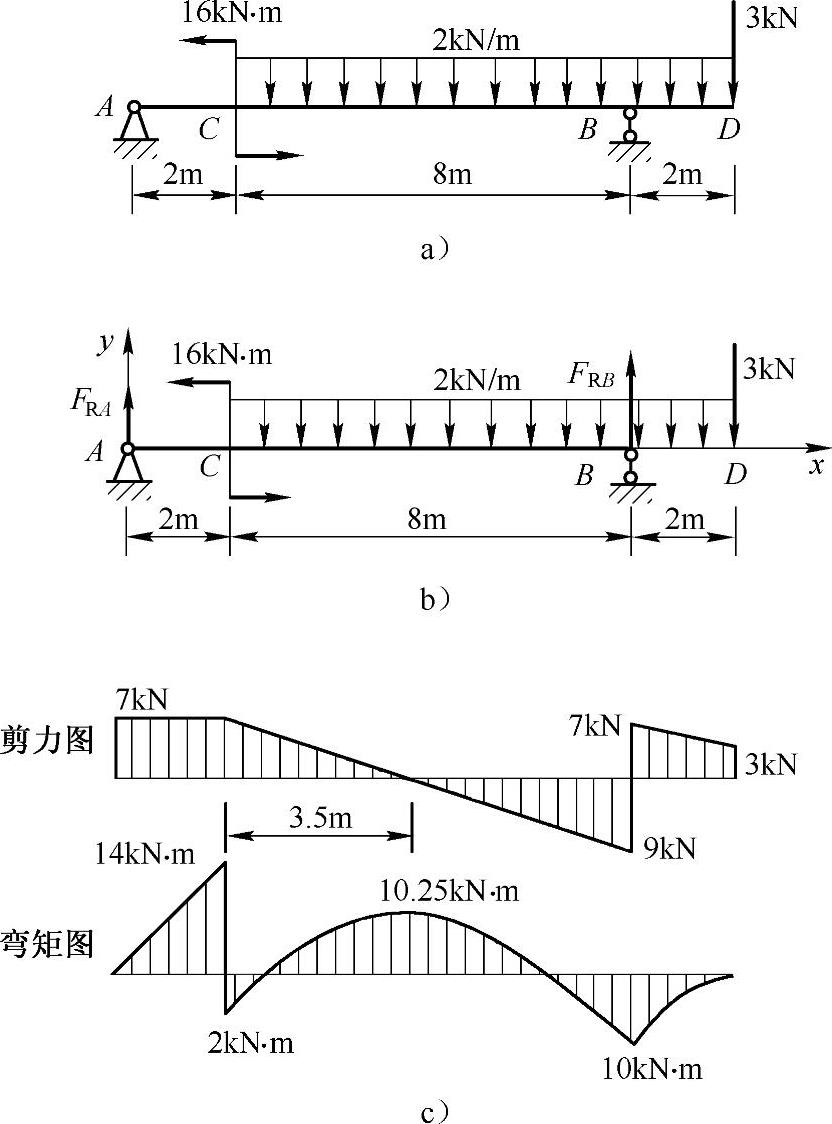
图4-1 例4-1图
解:(1)求支反力
ΣMB=0,16kN·m+(2kN/m)×8m×4m-FRA×10m-3kN×2m-(2kN/m)×2m×1m=0,得FRA=7kN
ΣFy=0,FRA+FRB-3kN-(2kN/m)×10m=0,得FRB=16kN
(2)求剪力方程和弯矩方程
选取坐标系如图4-1b所示。
AC段:
FS(x)=7(kN)(0<x<2)
M(x)=7x(kN·m)(0≤x<2)
CB段:
FS(x)=7-2(x-2)=11-2x(kN)(2<x<10)
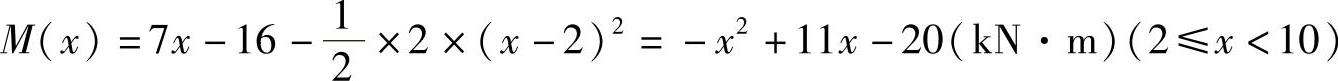
BD段:
FS(x)=27-2x(kN)(10<x<12)
M(x)=-x2+27x-180(kN·m)(10≤x<12)
(3)作剪力图和弯矩图
剪力图与弯矩图如图4-1c所示。
(4)最大剪力和最大弯矩
|FS|max=9kN,|M|max=14kN·m
例4-2 一端外伸的梁的尺寸及所受载荷如图4-2a所示,q和a均已知,试作梁的剪力图和弯矩图。
解:(1)求支反力
∑MA=0,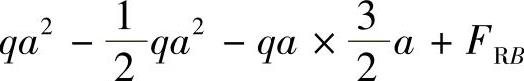
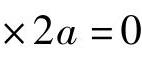 ,得
,得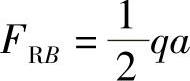
ΣFy=0,FRA+FRB-qa-qa=0,得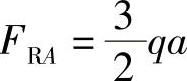
(2)求剪力方程和弯矩方程选取坐标系如图4-2b所示。
CA段:
FS=-qa(0<x<a)
M=-qax(0≤x<a)
AD段:
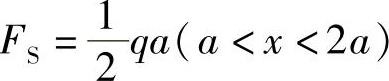
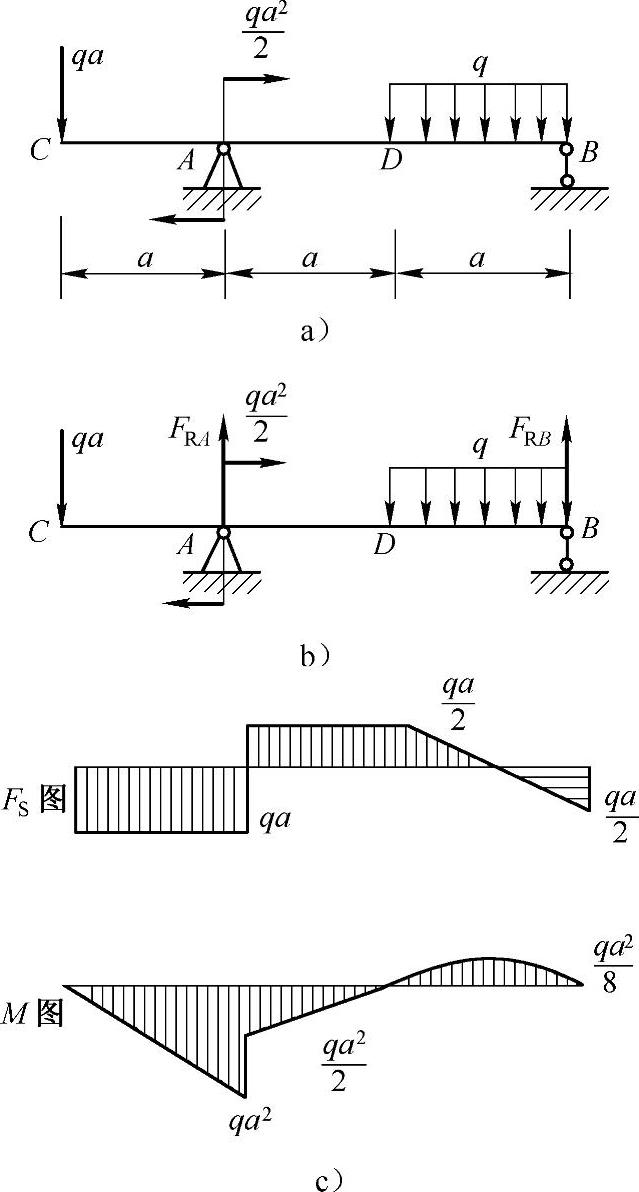
图4-2 例4-2图
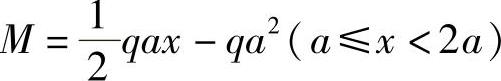
DB段:
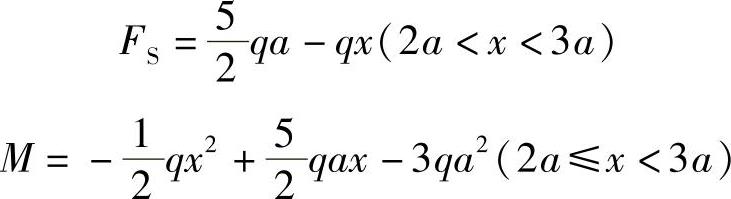
(3)作剪力图和弯矩图
剪力图与弯矩图如图4-2c所示。
例4-3 画出如图4-3a所示结构的剪力图和弯矩图。
解:(1)求支反力
ΣMA=0,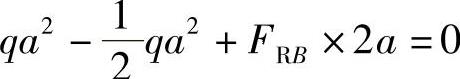 ,得
,得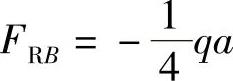 ΣFy=0,FRA+FRB-qa=0,得
ΣFy=0,FRA+FRB-qa=0,得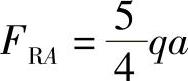
(2)求剪力方程和弯矩方程选取坐标系如图4-2b所示。
AC段:
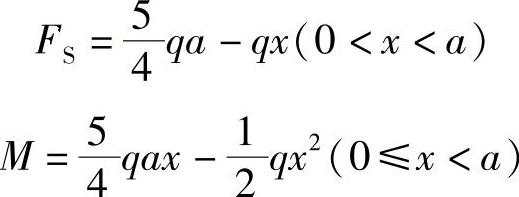
CB段:
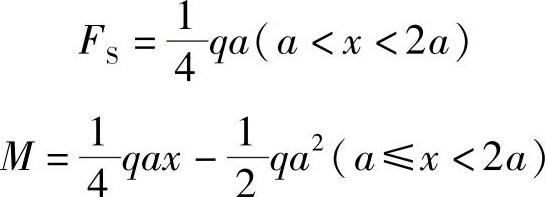
(3)作剪力图和弯矩图
剪力图与弯矩图如图4-3c所示。
例4-4 外伸梁及其所受载荷如图4-4a所示,试作梁的剪力图和弯矩图。
解:利用简易法作梁的剪力图和弯矩图如图4-4b所示。其中,x=1m处,Mmax=20.5kN·m。
例4-5 求如图4-5a所示刚架的最大剪力和最大弯矩。
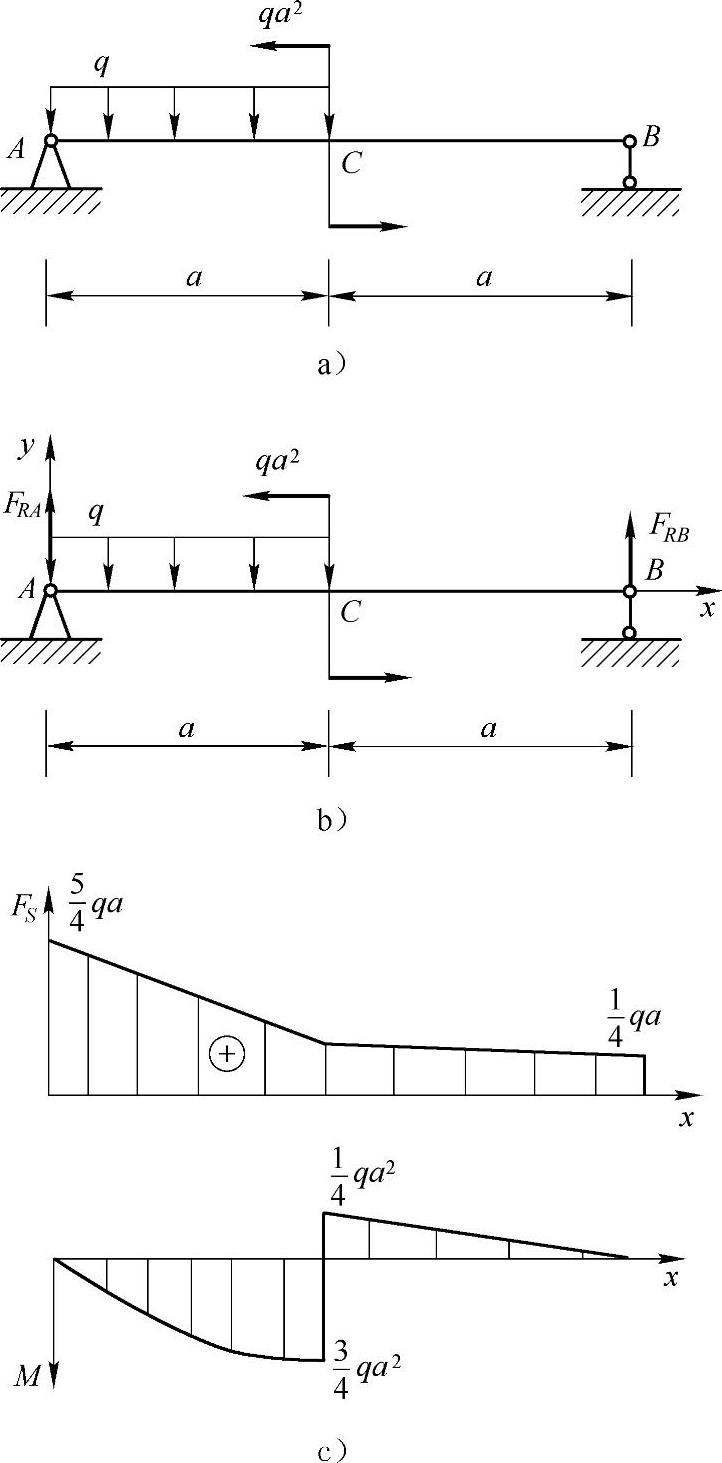
图4-3 例4-3图
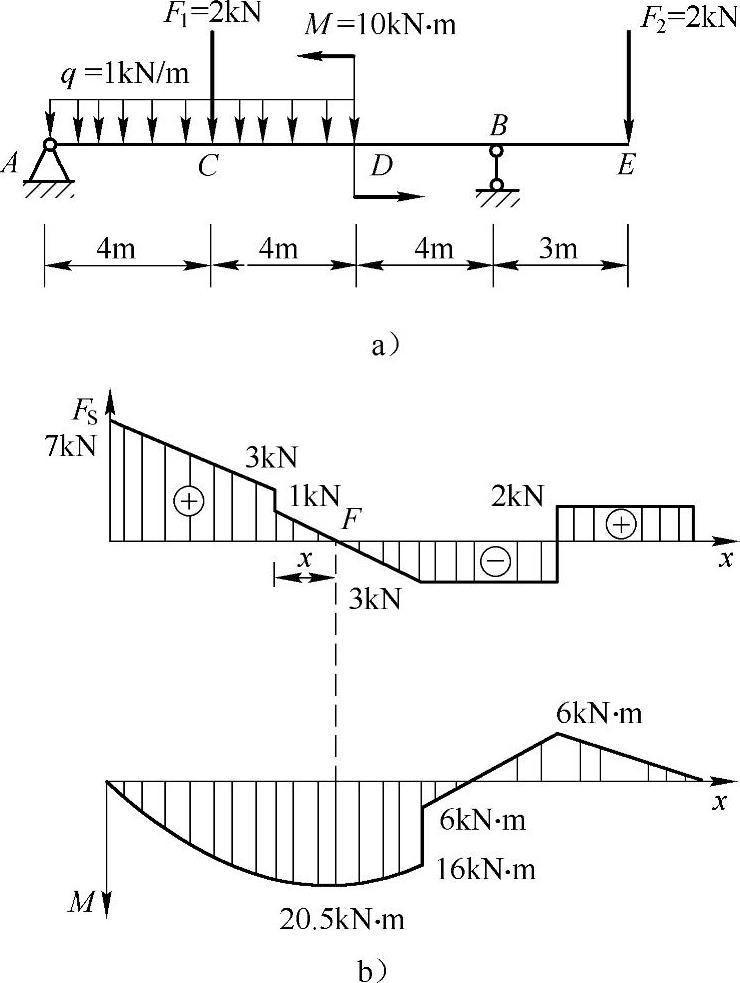
图4-4 例4-4图
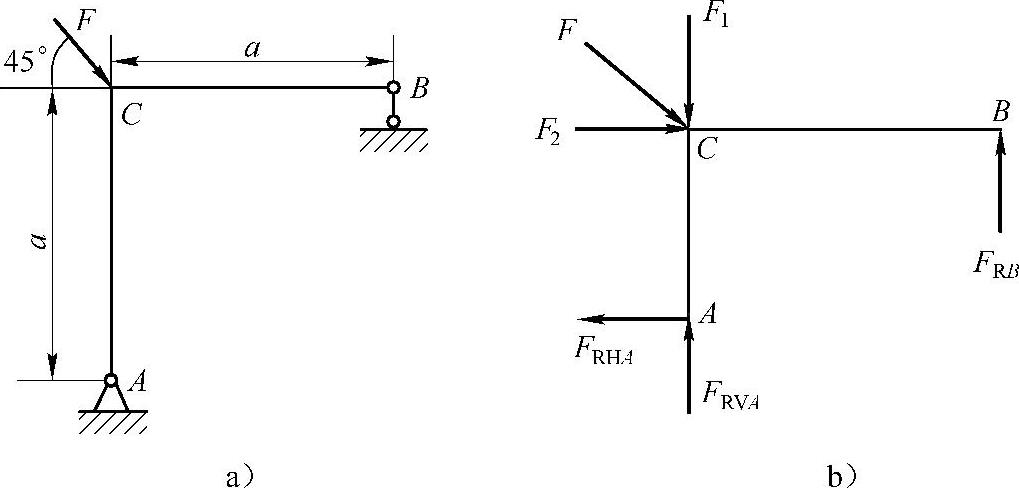
图4-5 例4-5图
解:(1)首先求支座反力,刚架的受力简图如图4-5b所示,力F分解为铅垂力F1和水平力F2,根据平衡方程
ΣFx=0,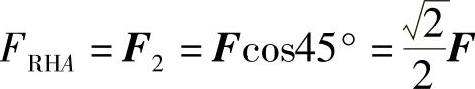
ΣMA=0,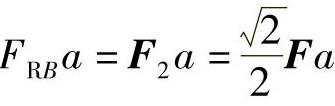 ,得
,得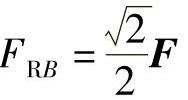
ΣFy=0,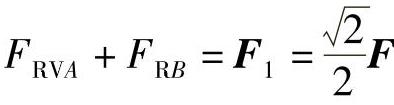 ,得FRVA=0
,得FRVA=0
(2)用截面法求刚架的内力,列出剪力方程和弯矩方程。在AC段内,设距A端为x的任一截面的剪力和弯矩分别为FS(x)和M(x),则
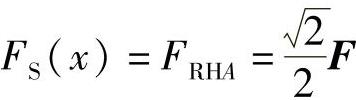 ,
,
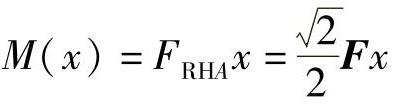
同理,对BC段,坐标原点取在B点,则距B点为x的任一截面的剪力和弯矩分别为FS(x)和M(x),则
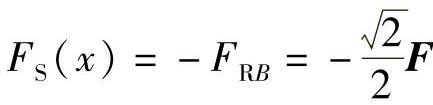 ,
,
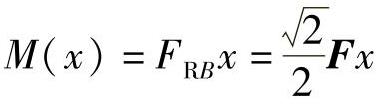
由此得到,最大剪力和最大弯矩分别为
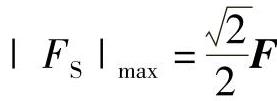 ,
,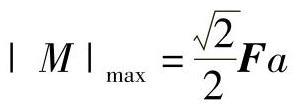
例4-6 作图4-6a中所示的梁的剪力图和弯矩图。
解:(1)作梁的受力图,如图4-6b所示。
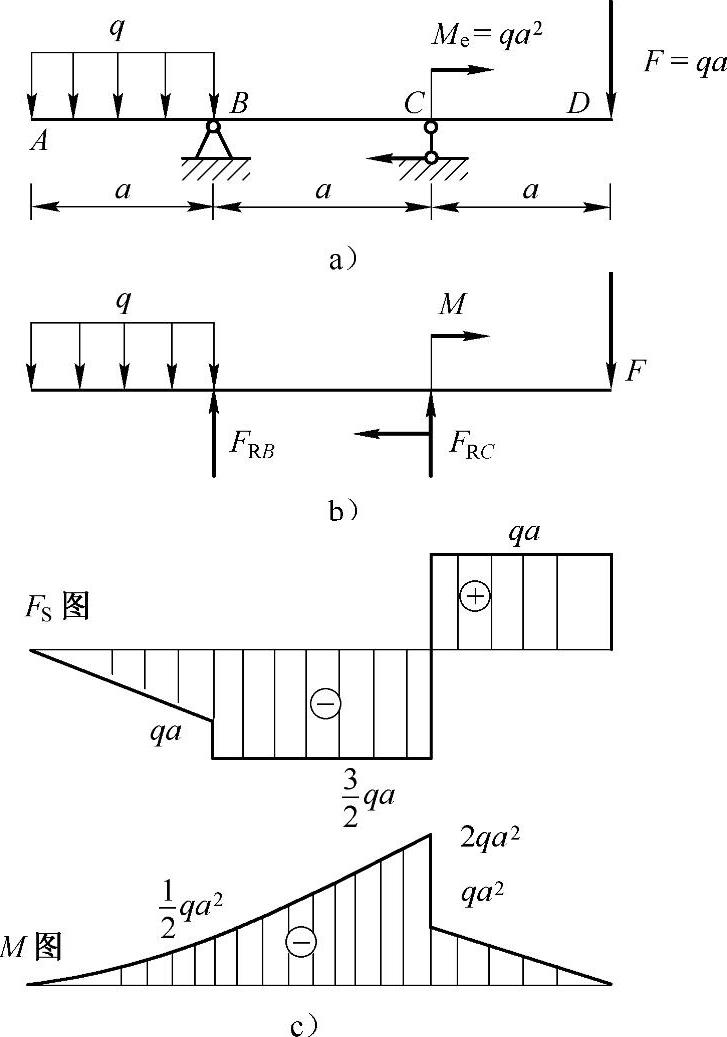
图4-6 例4-6图
由平衡方程
ΣMB=0,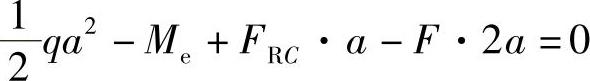 ,得
,得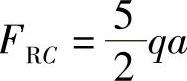
ΣFy=0,FRC+FRB-qa-F=0,得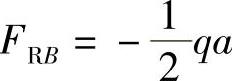
(2)作梁的剪力图和弯矩图如图4-6c所示。
例4-7 作图4-7a中所示的刚架的内力图。
解:(1)作刚架的受力图,如图4-7b所示。
由平衡方程
ΣME=0,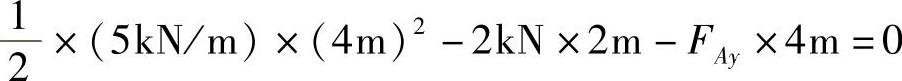 ,得FAy=9kN
,得FAy=9kN
ΣFx=0,得FEx=2kN
ΣFy=0,FAy+FEy-(5kN/m)×4m=0,得FEy=11kN
(2)作刚架的内力图分别如图4-7c、d、e所示。
例4-8 用截面法求如图4-8a所示悬臂梁C截面上的内力。
解:(1)沿C截面将梁截开,保留左段,受力图如图4-8b所示,C截面内力为剪力FSC和弯矩MC。
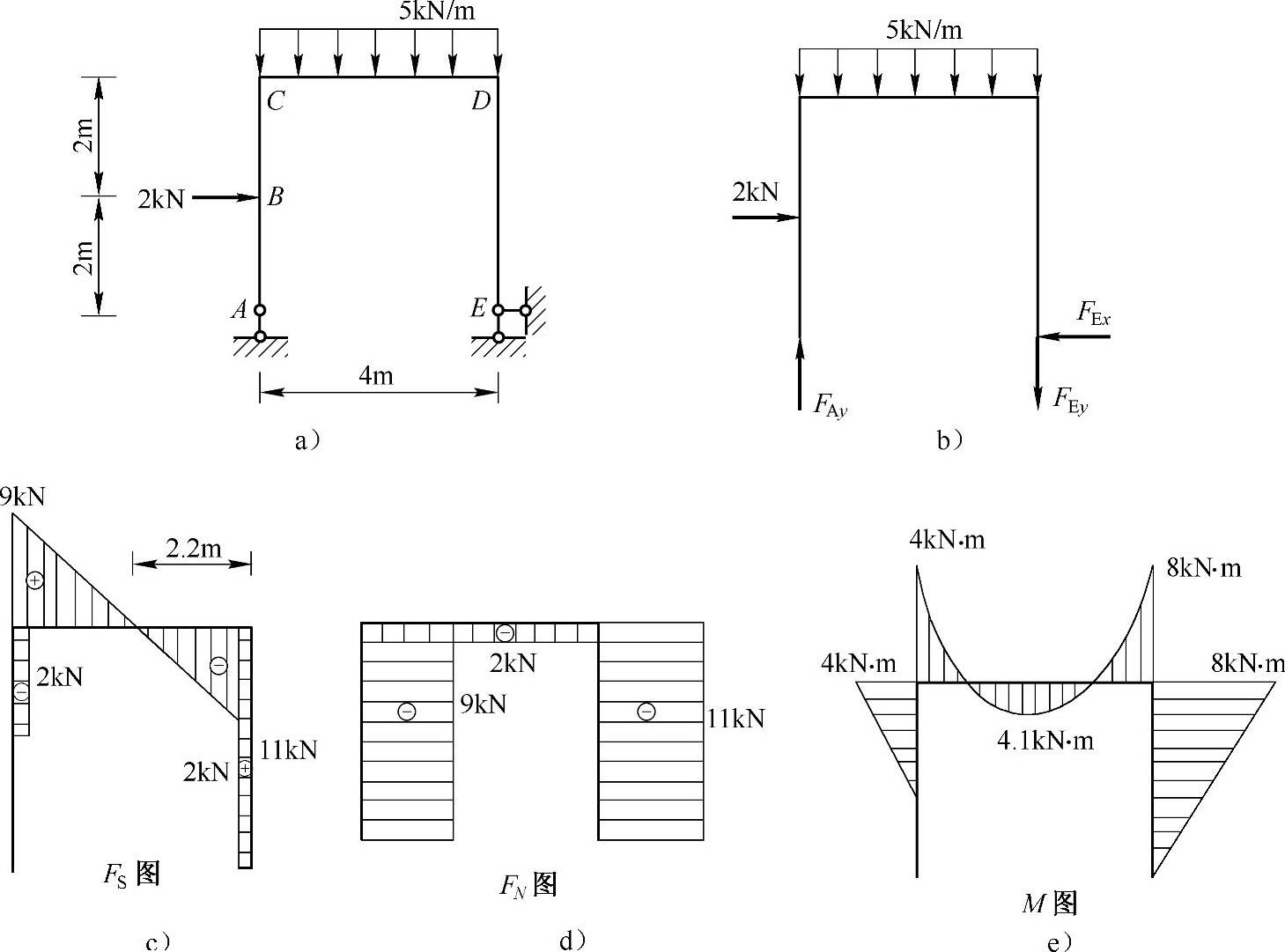
图4-7 例4-7图
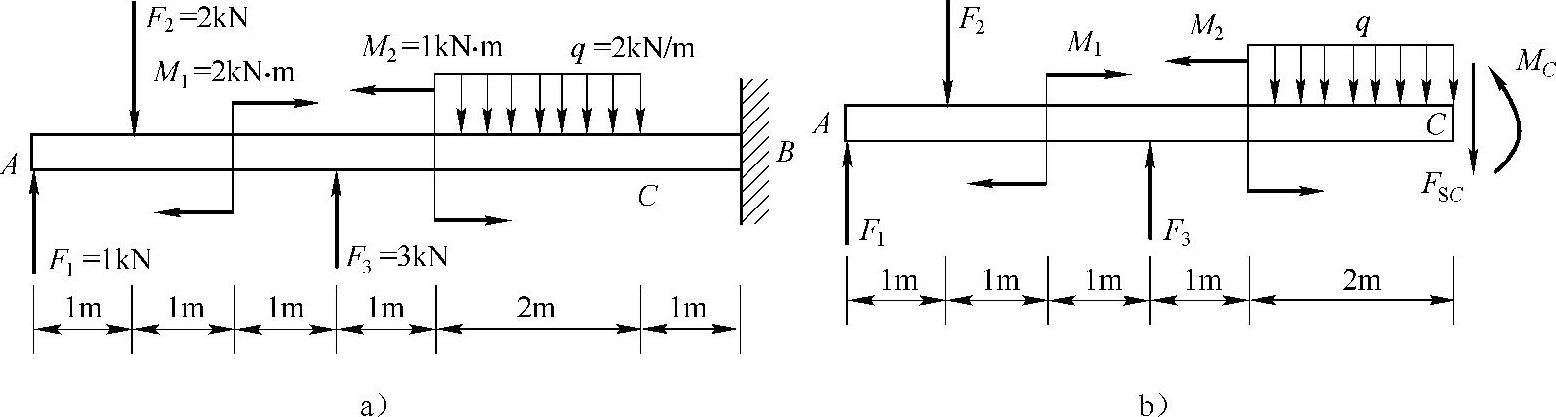
图4-8 例4-8图
(2)列静力平衡方程求C截面内力。
由平衡方程
ΣFy=0,F1-F2+F3-q×2m-FSC=0,得FSC=-2kN
ΣMC=0,-F1×6m+F2×5m-M1-F3×3m+M2+q×2m×1m+MC=0,得MC=2kN·m得
