8.3  例题解析

8.3 例题解析

例8-1 简支折线梁受力如图8-2a所示，截面为25cm×25cm的正方形截面，试求此梁的最大正应力。

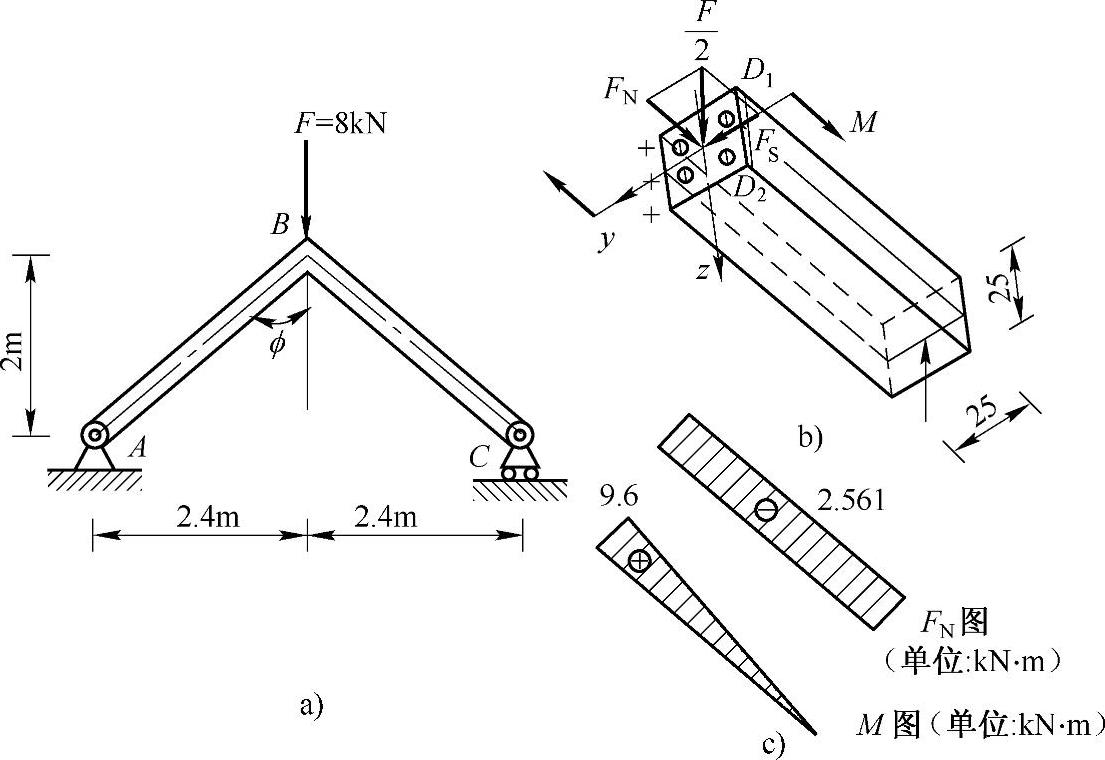
图8-2 例8-1图

解：（1）外力分析，判变形。由对称性可知，A，C两处的约束力为F/2，主动力、约束力均在纵向对称面内，简支折线梁将发生压弯组合变形。

（2）内力分析，判危险面。从下端无限靠近B处沿横截面将简支折线梁截开，取右边部分为研究对象，受力如图8-2b所示。梁上各横截面上轴力为常数，B横截面具有最大弯矩，故B横截面为压弯组合变形危险面。

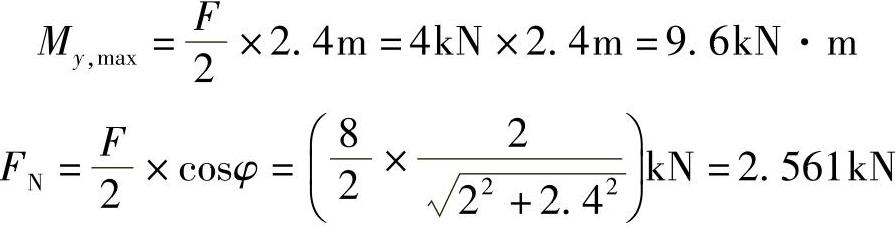
如图8-2c所示。

（3）应力分析，判危险点，如图8-2b所示。由于截面为矩形，而D₁D₂是压弯组合变形的压缩边缘，故危险面上D₁D₂边缘处出现最大压应力。且

例8-2 No.25普通热轧工字钢制成的立柱受力如图8-3所示。试求图示横截面上a，b，c，d四处的正应力。

解：查相应的表得

例8-3 起重构架如图8-4a所示，梁ACD由HT两根槽钢组成。已知a=3m，b=1m，F=30kN。梁材料的许用应力[σ]=170MPa。试选择槽钢的型号。

解：（1）外力分析：梁的计算简图如图8-4b所示，外力在纵向对称面内与轴斜交，故梁AC段发生拉伸与弯曲的组合变形。对A取矩，则BC杆所受压力为

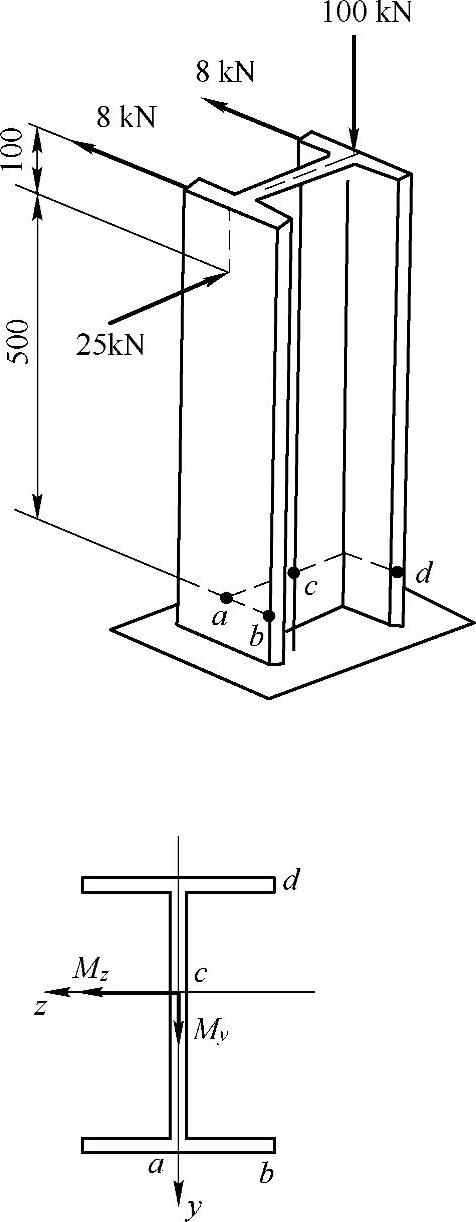
图8-3 例8-2图

（2）内力分析：轴力图、弯矩图如图8-4c、d所示。C左截面轴力和弯矩同时达到最大，是危险面。

F_N=69.28kN，|M|_max=30kN·m

（3）应力分析，判危险点：由于发生的是拉弯组合变形，加之截面有两个对称轴，危险面的上边缘具有最大拉应力，比下边缘的最大压应力的绝对值大，上边缘上各点正应力最大。

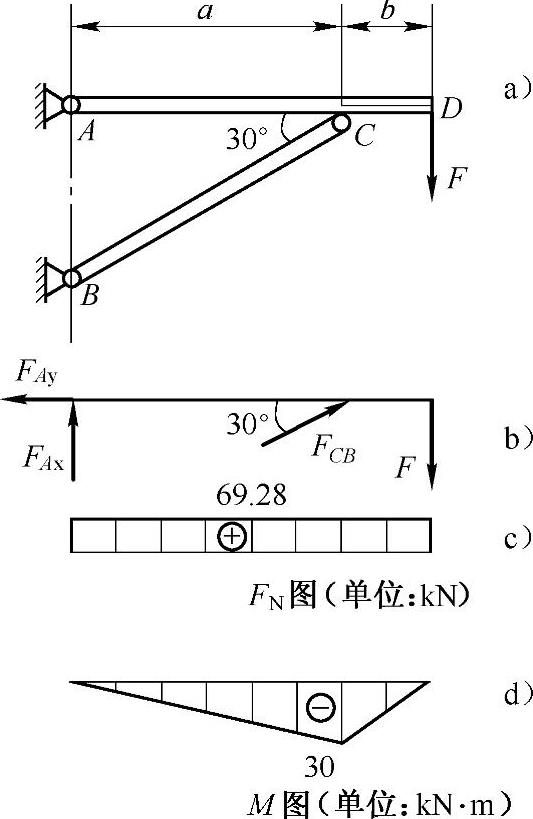
图8-4 例8-3图

（4）强度计算，选择槽钢的型号：

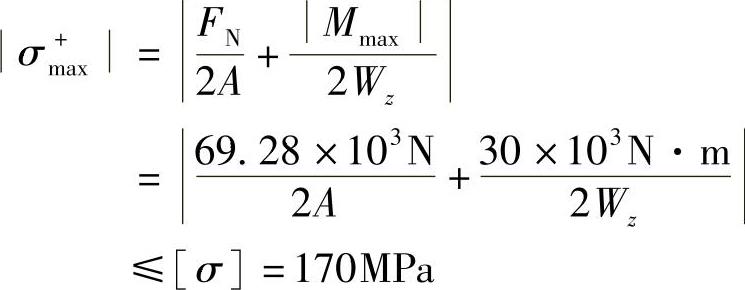
1）忽略轴力项的正应力，仅由弯曲项选择槽钢的型号：

查表可知A=21.95cm²，W_z=108.3cm³

2）对所选槽钢进行校核：

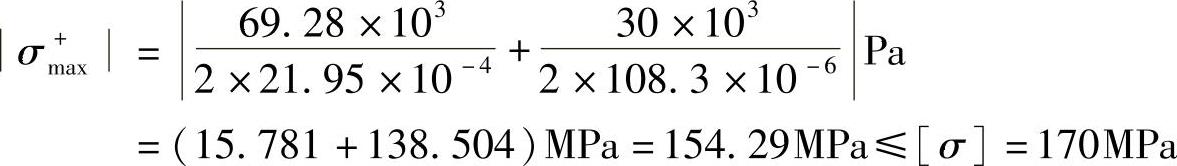
故所选择16槽钢能满足强度要求。

例8-4 如图8-5a所示，轴上安装两个圆轮，F、W分别作用在两轮上，并沿铅垂方向。轮轴处于平衡状态。若轴的直径d=110mm，许用应力[σ]=60MPa。试按第四强度理论确定许用载荷F。

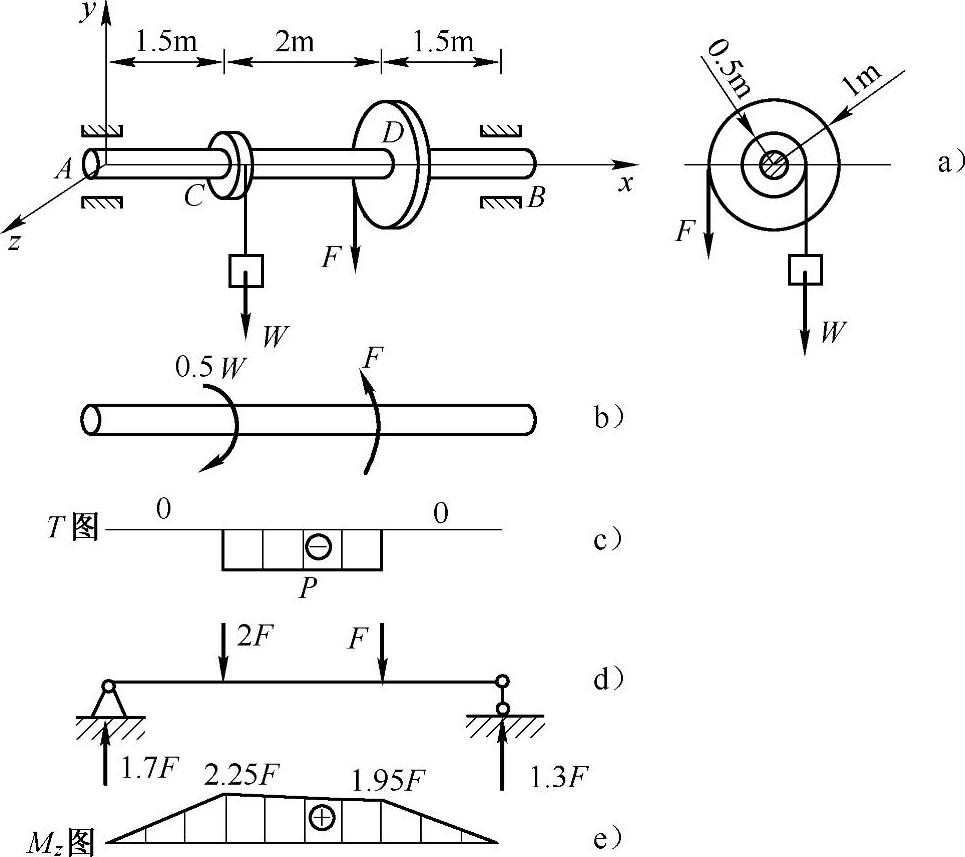
图8-5 例8-4图

解：（1）外力分析，判变形。

力F、W向轴线平移，必附加引起扭转的力偶，受力如图8-5b所示；平移到轴线的外力使轴在铅垂平面内上下弯曲。外力沿竖直方向与轴异面垂直，使轴发生扭转与弯曲的组合变形。

1）由于轴平衡，故

ΣM_x（F）=0，-F×1m+W×0.5m=0，W=2F

2）将轴进行简化，计算简图如图8-5d所示，求铅垂面内梁的约束力

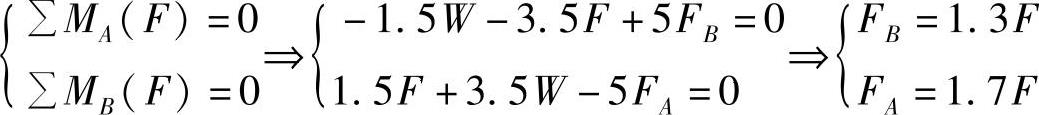
（2）内力分析，判危险面。

扭矩图、弯矩图如图8-5c、e所示，C的右截面是危险面：

M_z，max=2.25P，T=F

（3）应力分析。

M_z使C横截面上下边缘点弯曲正应力最大，同时又有最大的扭转切应力，故C的右截面上下边缘点是强度理论的危险点。

（4）按第四强度理论求许用载荷。

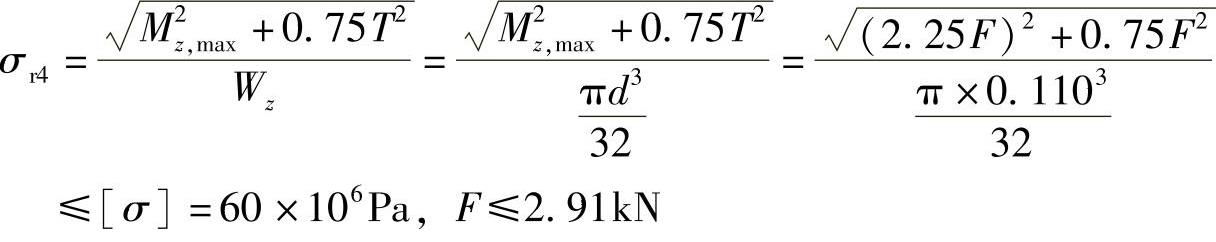
例8-5 传动轴如图8-6a所示，A轮受铅垂力F₁作用，直径D₁=200mm，F₁=2kN；B轮受水平拉力F₂作用，D₂=100mm。轴材料的许用应力[σ]=80MPa。已知轮轴处于平衡状态。（1）画出轴的扭矩图和弯矩图。（2）试按第三强度理论设计轴的直径，单位为mm。

解：（1）外力分析，判变形。

与轴异面垂直的外力F₁，F₂向轴线平移，必附加引起扭转的力偶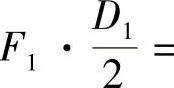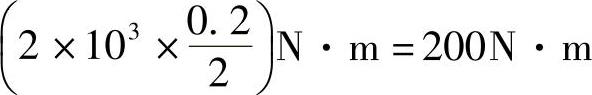；力平移后使轴发生方位难以确定的平面弯曲，总之轴发生弯扭组合变形。

（2）内力分析，判危险面。

将轴进行简化，计算简图如图8-6b、d、f所示，扭矩图、弯矩图如图8-6c、e、g所示，B的左截面合成的弯矩最大，是危险面。

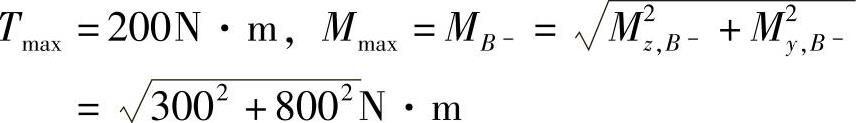
（3）按第三强度理论设计轴的直径d。

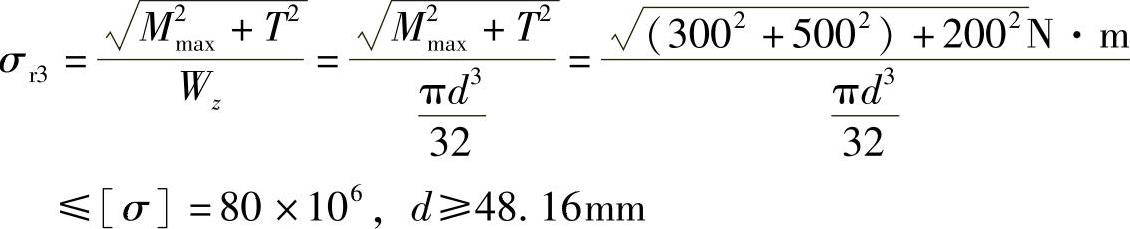
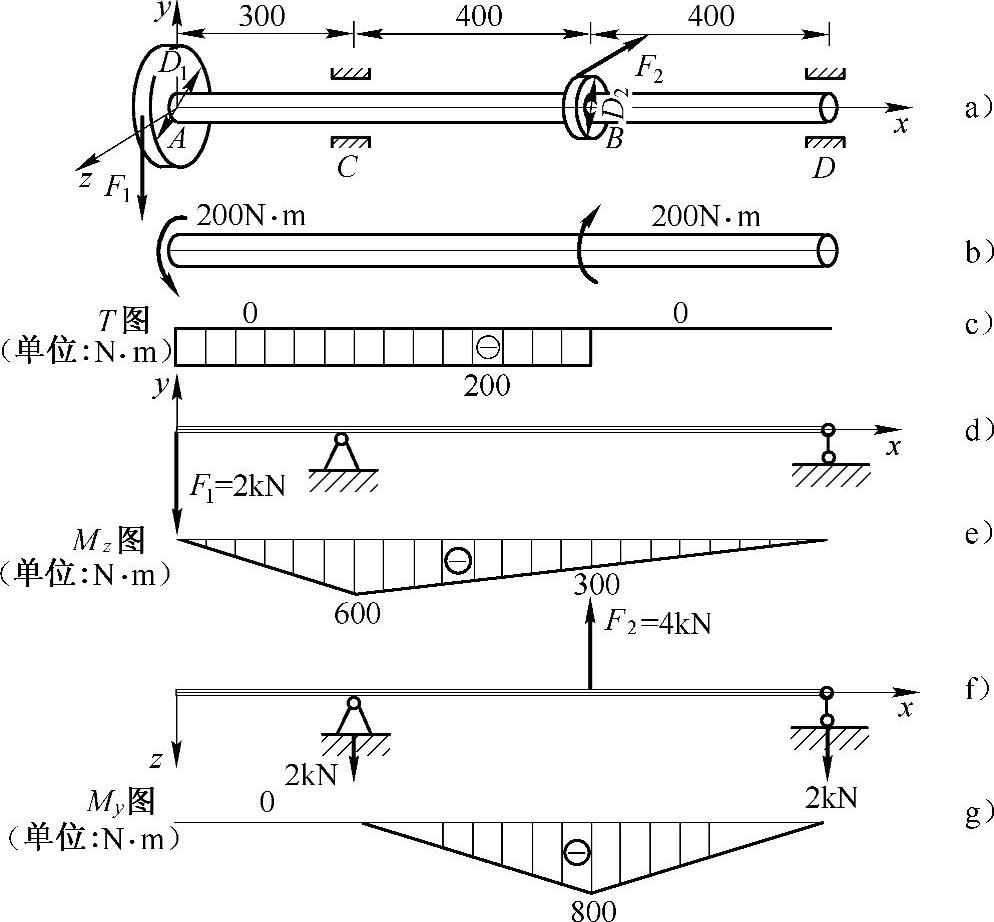
图8-6 例8-5图

例8-6 14工字钢悬臂梁受力情况如图8-7所示。已知l=0.8m，F₁=2.5kN，F₂=1.0kN，试求危险截面上的最大正应力。

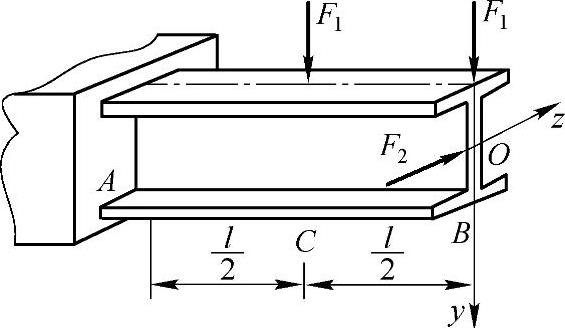
图8-7 例8-6图

解：危险截面在固定端，且

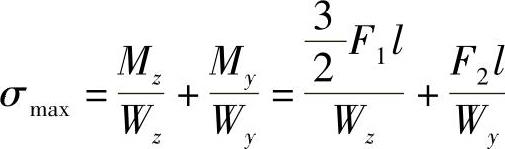
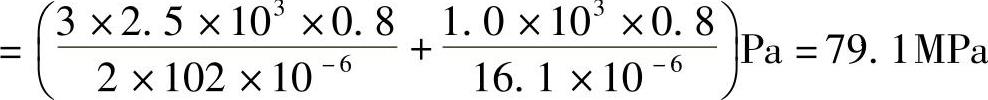
例8-7 受集度为q的均布载荷作用的矩形截面简支梁，其载荷作用面与梁的纵向对称面间的夹角为α=30°，如图8-8所示。已知该梁材料的弹性模量E=10GPa；梁的尺寸为l=4m，h=160mm，b=120mm；许用应力[σ]=12MPa；许可挠度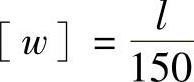。试校核梁的强度和刚度。

解：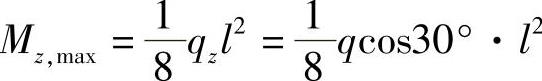

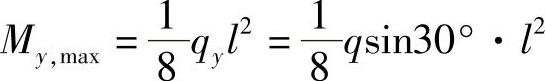
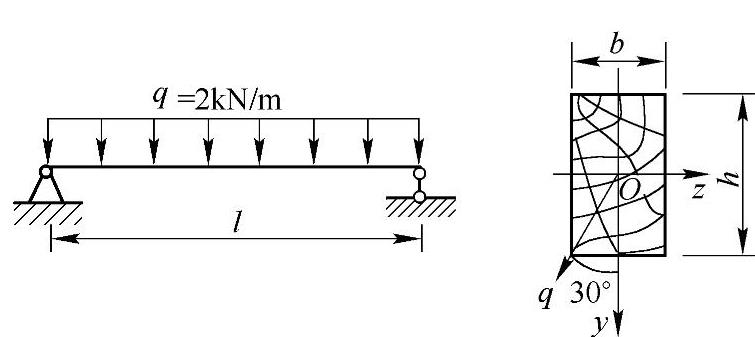
图8-8 例8-7图

例8-8 图8-9a所示的齿轮传动装置中，Ⅱ轴的受力情况及尺寸如图8-9b所示。轴上大齿轮1的半径r₁=85mm，受切周向力F_t1和径向力F_t1作用，且F_r1=0.364F_t1；小齿轮2的半径r₂=32mm，受切周向力F_t2和径向力F_r2作用，且F_r2=0.364F_t2。已知轴工作时传递的功率P=73.5kW，转速n=2000r/min，轴的材料为合金钢，其许用应力[σ]=150MPa。试按第三强度理论计算轴的直径。

解：Ⅱ轴的受力如图8-9c所示。

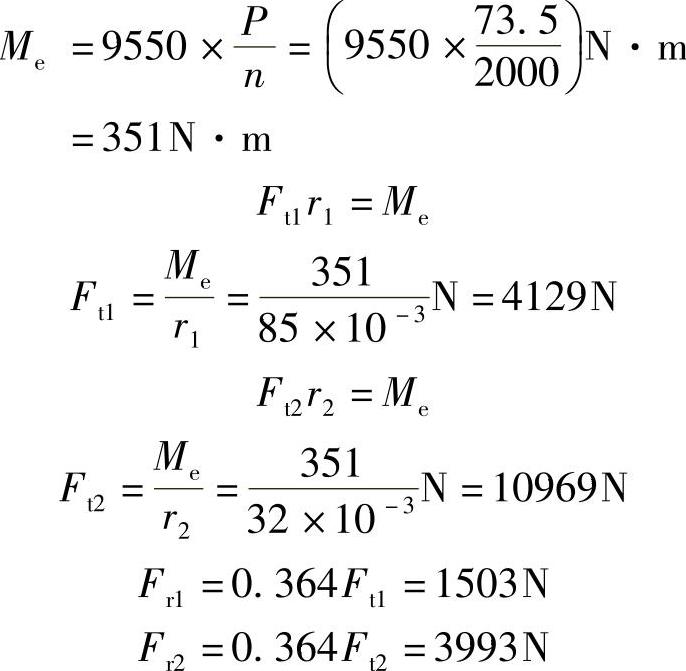
由ΣM_z=0，得

-F_Ay×280mm+F_r1×245mm+F_r2×65mm=0

即

-F_Ay×280mm+1503N×245mm+3993N×65mm=0

则 F_Ay=2242N

由 ΣF_y=0，得

F_Ay-F_r1-F_r2+F_By=0

则 F_By=3254N

由ΣM_y=0，得

F_Az×280mm-F_t1×245mm+F_t2×65mm=0

则 F_Az=1067N

由ΣF_z=0，得

F_Az-F_t1+F_t2+F_Bz=0

则 F_Bz=-7907N

M_Cy=F_Az×（35×10^-3m）=37.3N·m

M_Cz=F_Ay×（35×10^-3m）=78.5N·m

M_Dy=F_Bz×（65×10^-3m）=514N·m

M_Dz=F_By×（65×10^-3m）=212N·m

CD段扭矩T=：M_e=351N·m

作扭矩、弯矩图，如图8-9d所示危险截面为D左截面，则

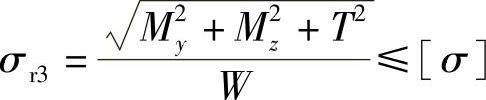
即

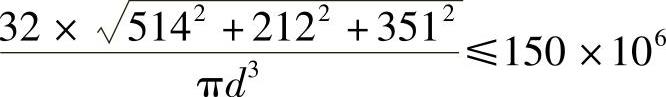
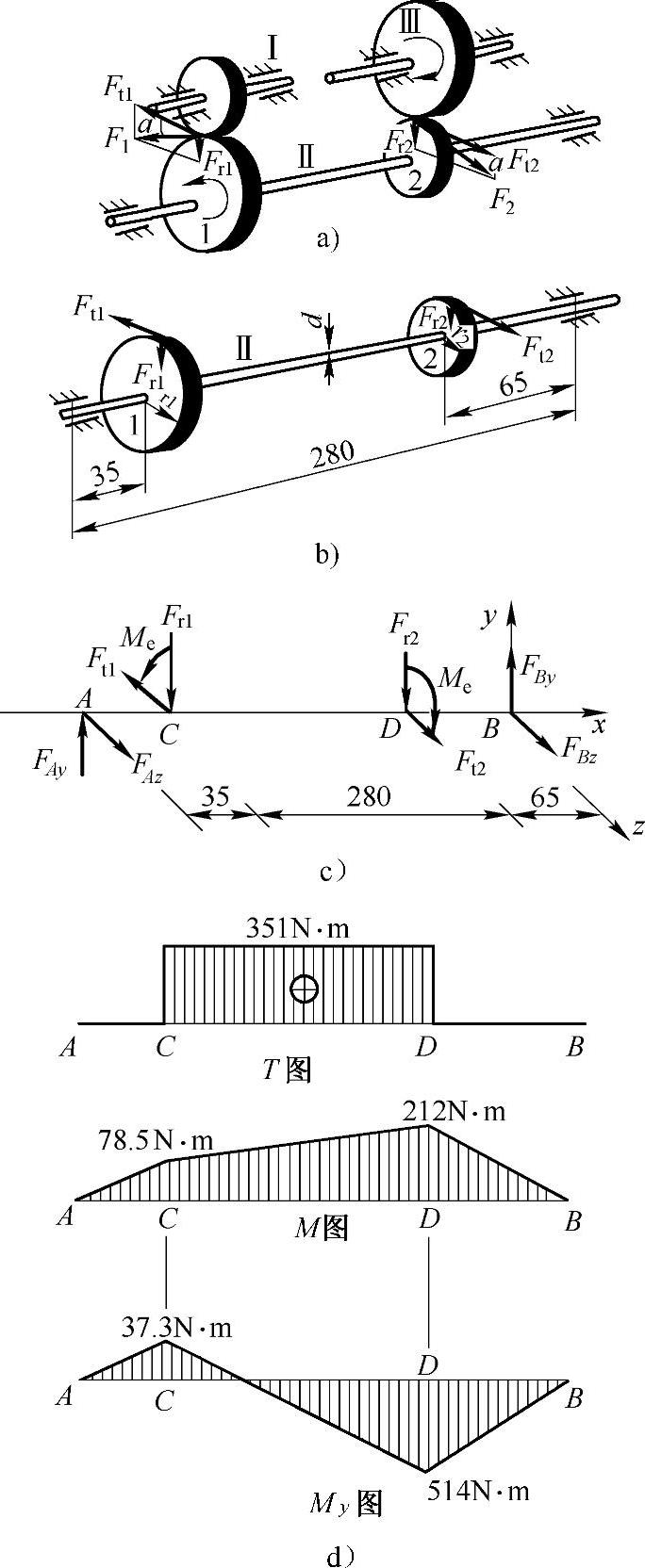
图8-9 例8-8图

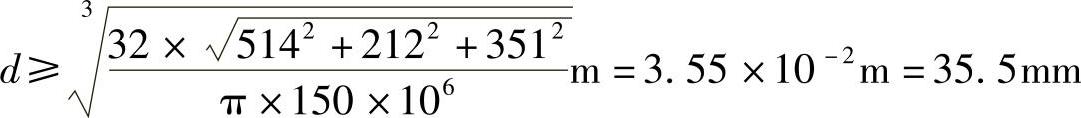
例8-9 直径d=40mm的实心钢圆轴，在某一横截面上的内力分量如图8-10所示。已知此轴的许用应力[σ]=150MPa。试按第四强度理论校核轴的强度。

解：（1）内力分析。

轴向拉伸使横截面有轴力F_N，而圆轴发生上下弯曲才会产生前后纵向对称面的弯矩M_y，而圆轴发生扭转变形才会产生力偶作用面与横截面平行的扭矩M_x。故此圆轴发生拉弯扭组合变形。

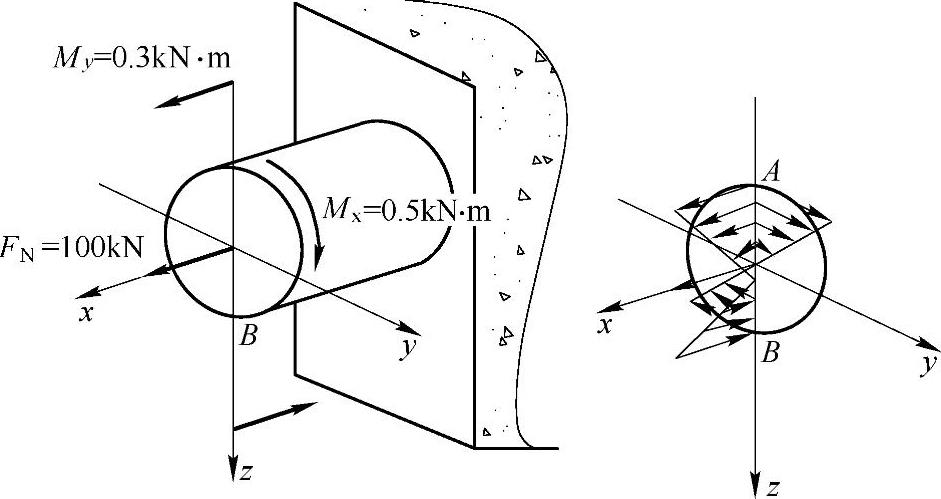
图8-10 例8-9图

（2）应力分析。

M_y使圆轴上下弯曲，A，B两点分别拥有最大的拉、压弯曲正应力；M_x使圆轴横截面上距圆心最远的周周上各点具有最大的扭转切应力；F_N使圆轴横截面上各点具有大小相同的拉应力。故A是拉弯扭组合变形的强度理论危险点。且

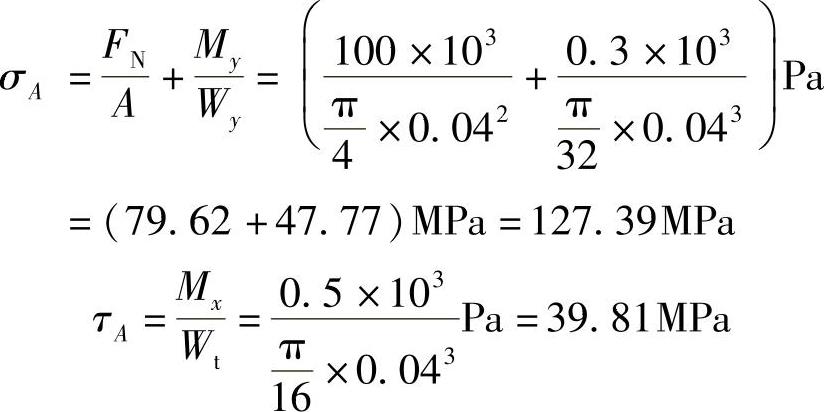
（3）按第四强度理论校核轴的强度。

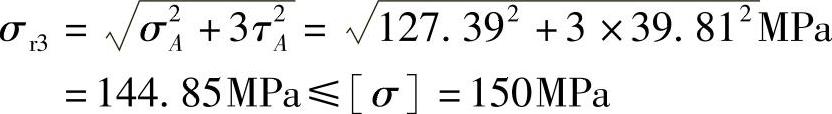
故强度足够。