6.1.3  挠曲线近似微分方程及其积分

（1）挠曲线近似微分方程

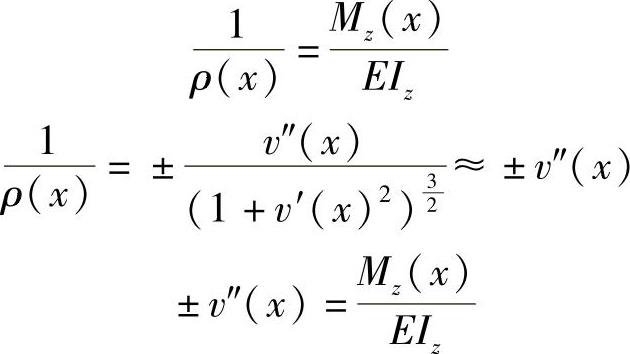
其中，正负号取决于弯矩正负号的规定以及坐标系的选择。

（2）用积分法求梁的变形

将挠曲线近似微分方程积分两次，得转角方程和挠曲线方程分别为

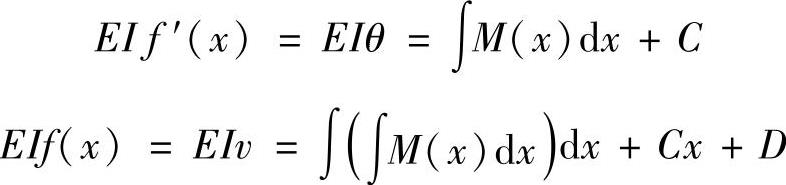
式中，C与D为积分常数，可利用梁的支座约束条件和挠曲线及转角方程必须连续的条件确定。这些条件称为确定积分常数的边界条件。

积分法是分析梁位移的基本方法。在梁的弯矩方程或抗弯刚度不连续处，应分段建立挠曲线近似微分方程，并分段积分（如分n段，则积分常数共有2n个）。在分段处，挠曲线应光滑（转角连续）、连续，即分段截面两侧具有相同的挠度与转角。优点：使用范围广，直接求出较精确的结果；缺点：计算较繁。