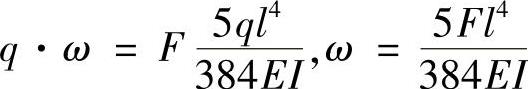首页> 图书频道> 工学> 工业技术

12.3  例题解析

2025年10月13日
版权
12.3 例题解析

例12-1 计算图12-1所示梁或结构内的应变能。略去剪切的影响，EI为已知。对于只受拉伸（或压缩）的杆件，考虑拉伸（压缩）时的应变能。

解：a）梁的弯矩方程为

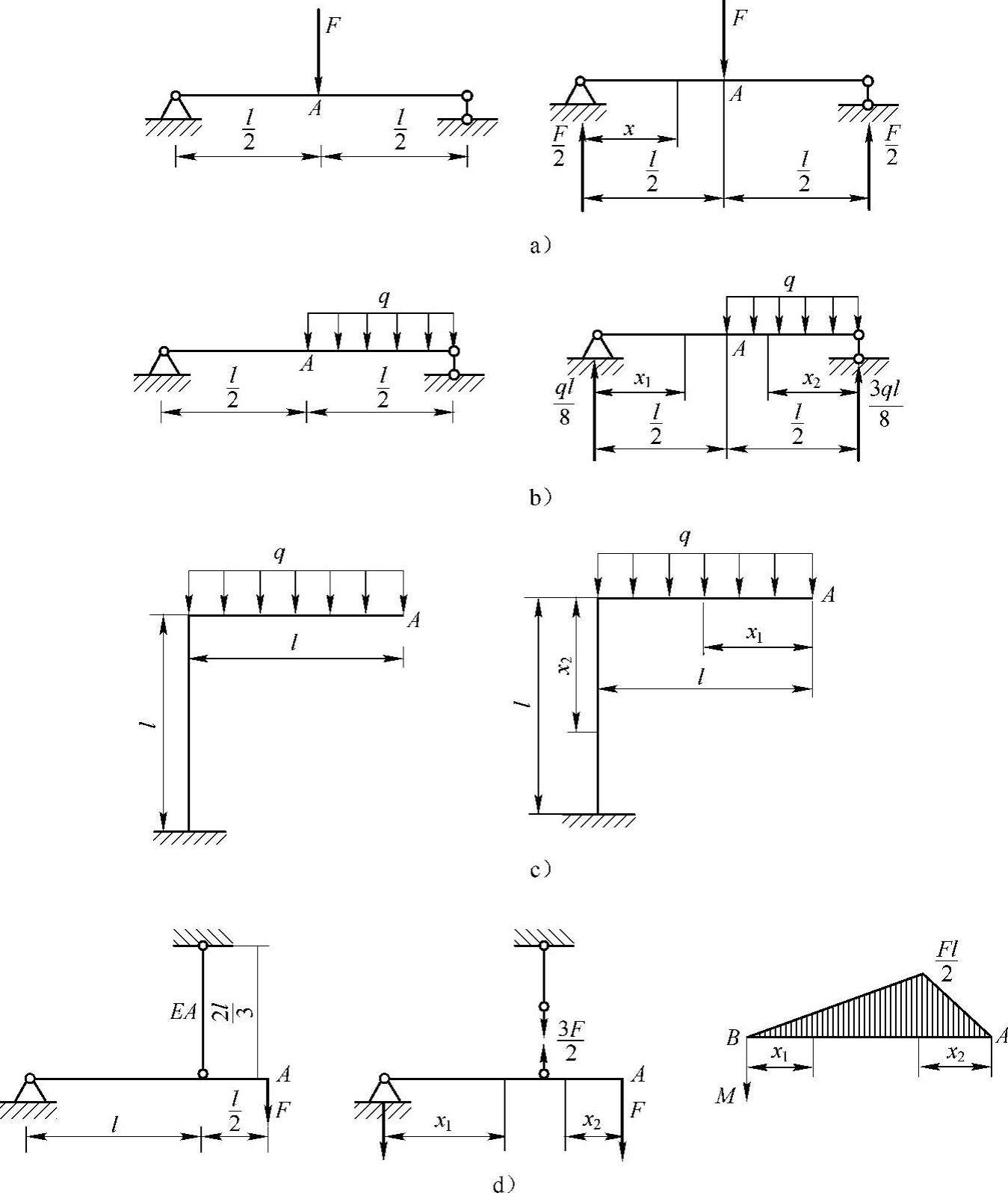
978-7-111-43425-2-Chapter12-20.jpg

图12-1 例12-1图

978-7-111-43425-2-Chapter12-21.jpg

利用对称性，得梁的弯曲应变能为

978-7-111-43425-2-Chapter12-22.jpg

b）梁的弯矩方程为

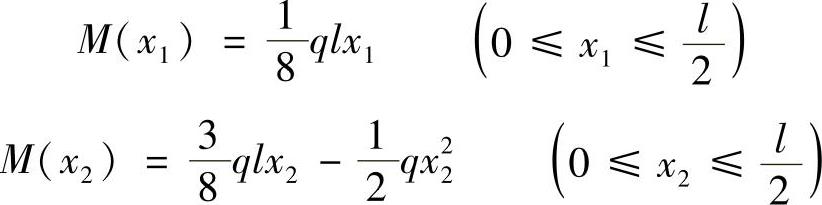
978-7-111-43425-2-Chapter12-23.jpg

梁的应变能为

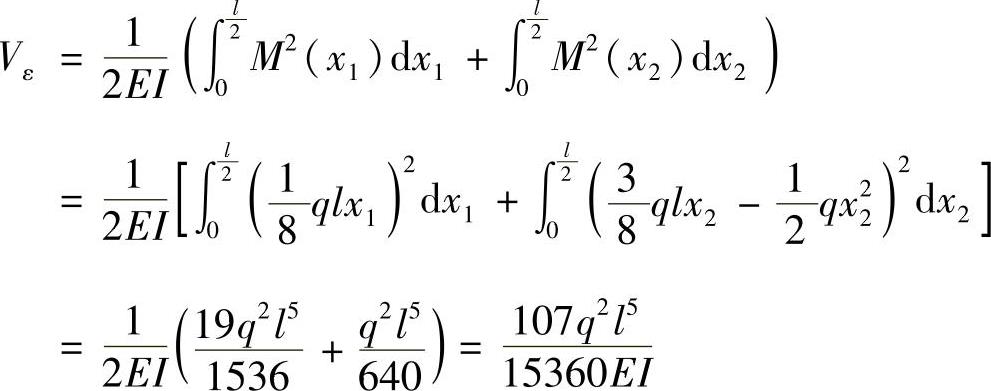
978-7-111-43425-2-Chapter12-24.jpg

c）刚架的弯矩方程为

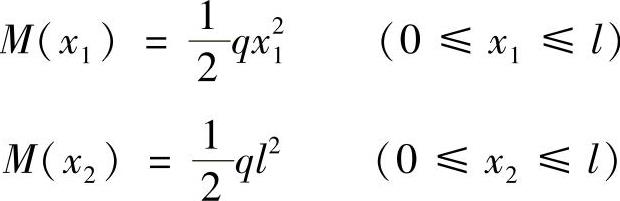
978-7-111-43425-2-Chapter12-25.jpg

刚架的应变能为

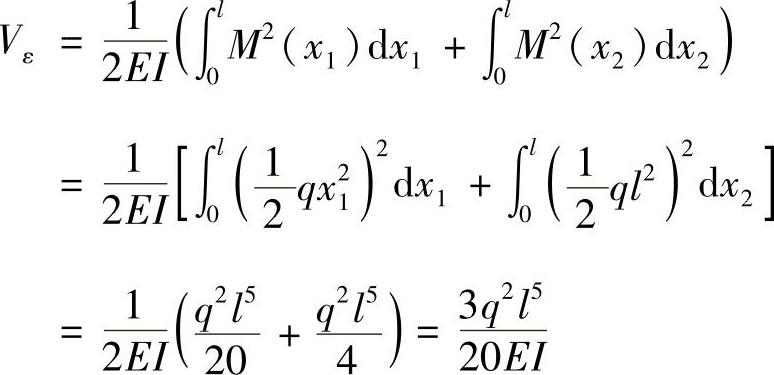
978-7-111-43425-2-Chapter12-26.jpg

d）结构中梁的弯矩方程为

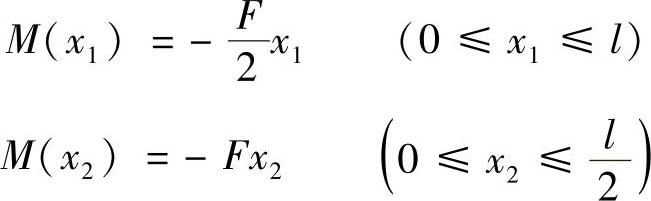
978-7-111-43425-2-Chapter12-27.jpg

拉杆的轴力为 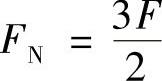978-7-111-43425-2-Chapter12-28.jpg

结构的应变能等于梁的弯曲应变能与拉杆的拉伸应变能的和，即

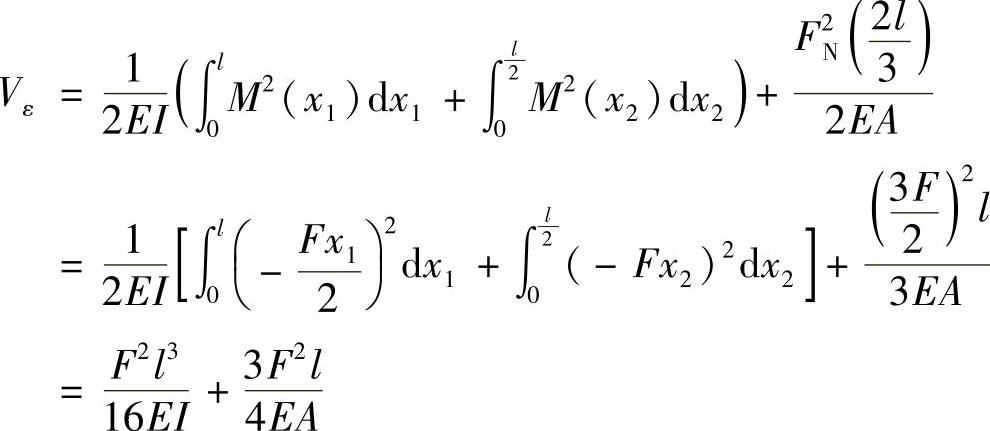
978-7-111-43425-2-Chapter12-29.jpg

例12-2 试求图12-2所示受扭圆轴内的应变能（d2=1.5d1）。

解：应变能为

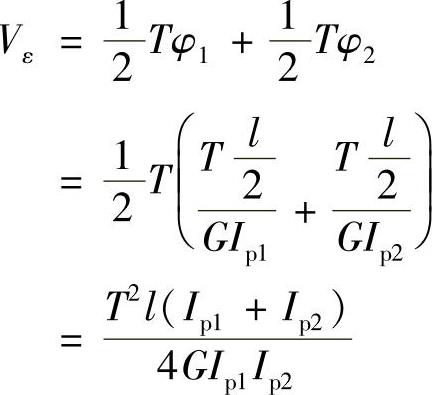
978-7-111-43425-2-Chapter12-30.jpg

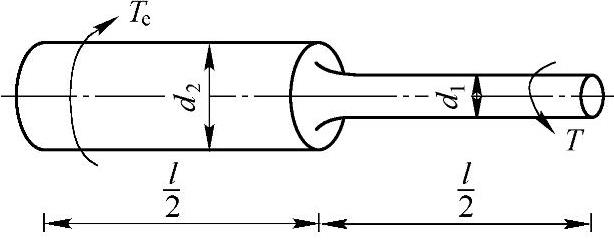
978-7-111-43425-2-Chapter12-31.jpg

图12-2 例12-2图

其中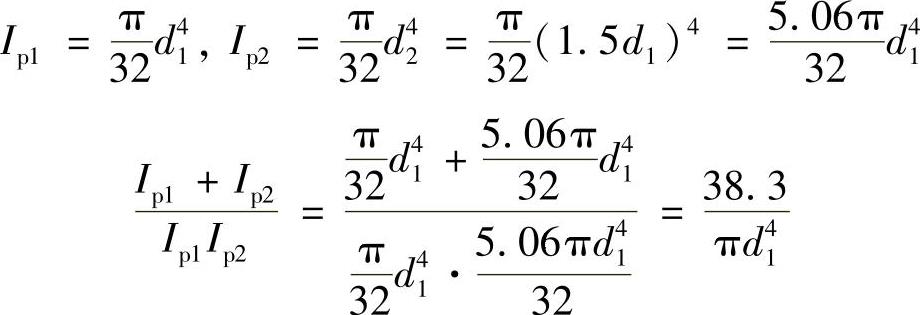，978-7-111-43425-2-Chapter12-32.jpg

因此 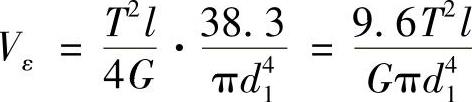978-7-111-43425-2-Chapter12-33.jpg

例12-3 应用能量法计算图12-3a所示梁中点的转角。

解：（1）外力分析，如图12-3b所示。

（2）内力分析，有

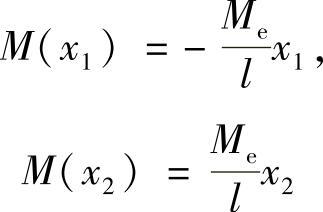
978-7-111-43425-2-Chapter12-34.jpg

（3）应变能和外力功计算，即

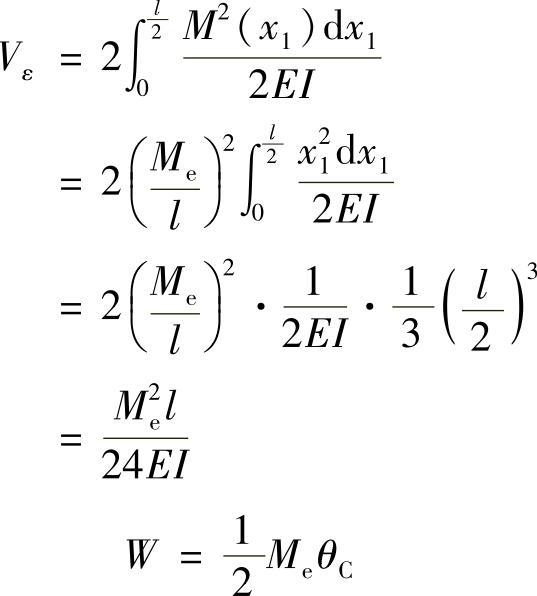
978-7-111-43425-2-Chapter12-35.jpg

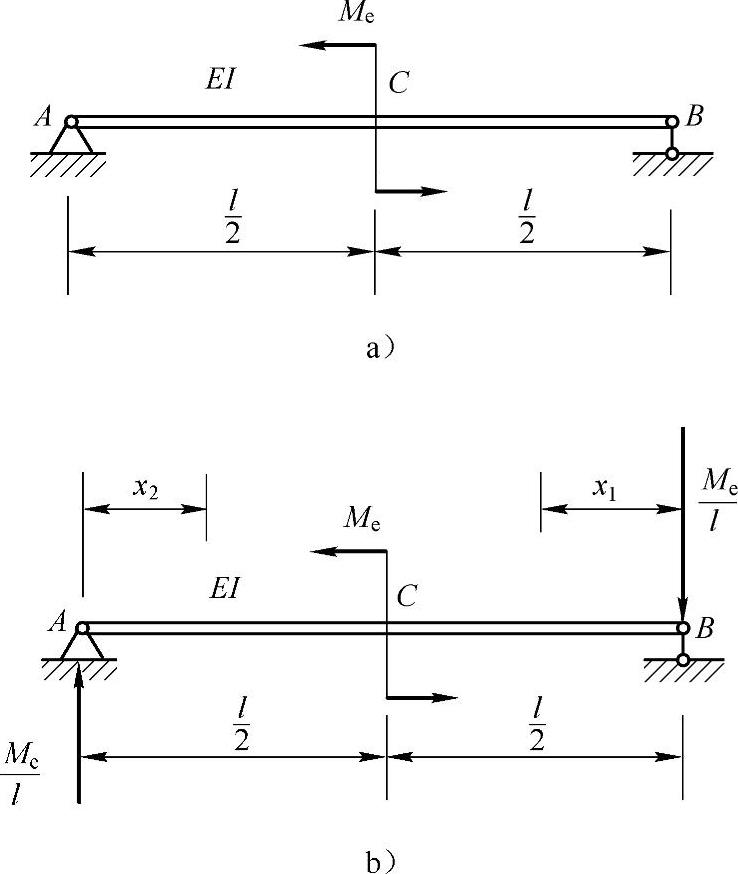
978-7-111-43425-2-Chapter12-36.jpg

图12-3 例12-3图

（4）应用能量法计算转角，由

W=Vε

得

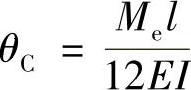
978-7-111-43425-2-Chapter12-37.jpg

例12-4 试用卡氏定理求图12-4所示各刚架截面A的位移和截面A，B的转角。略去剪力FS和轴力FN的影响，EI为已知。

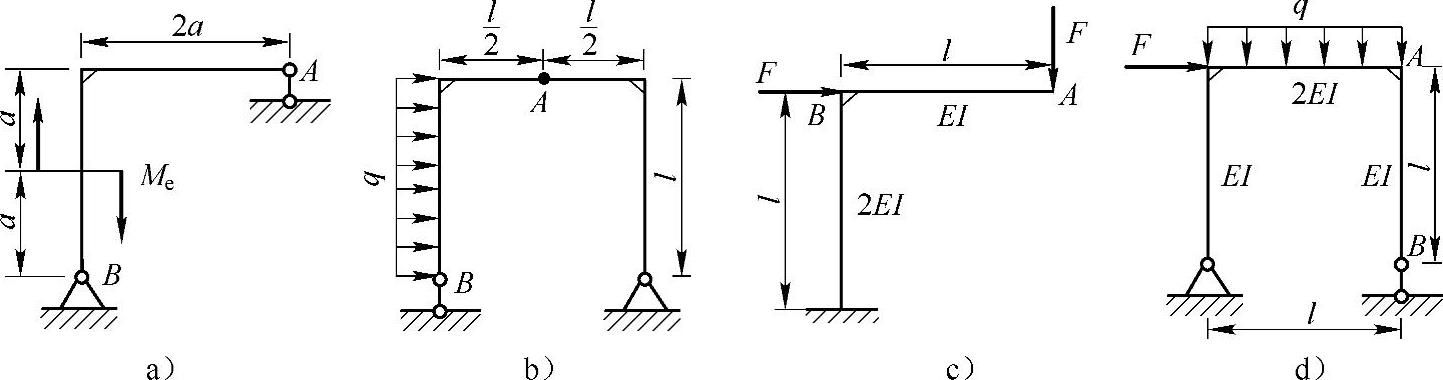
978-7-111-43425-2-Chapter12-38.jpg

图12-4 例12-4图

解：12-4a：

（1）求截面A的水平位移ΔHA。

截面A处添加一水平集中载荷F，如图12-5a所示，刚架的应变能为

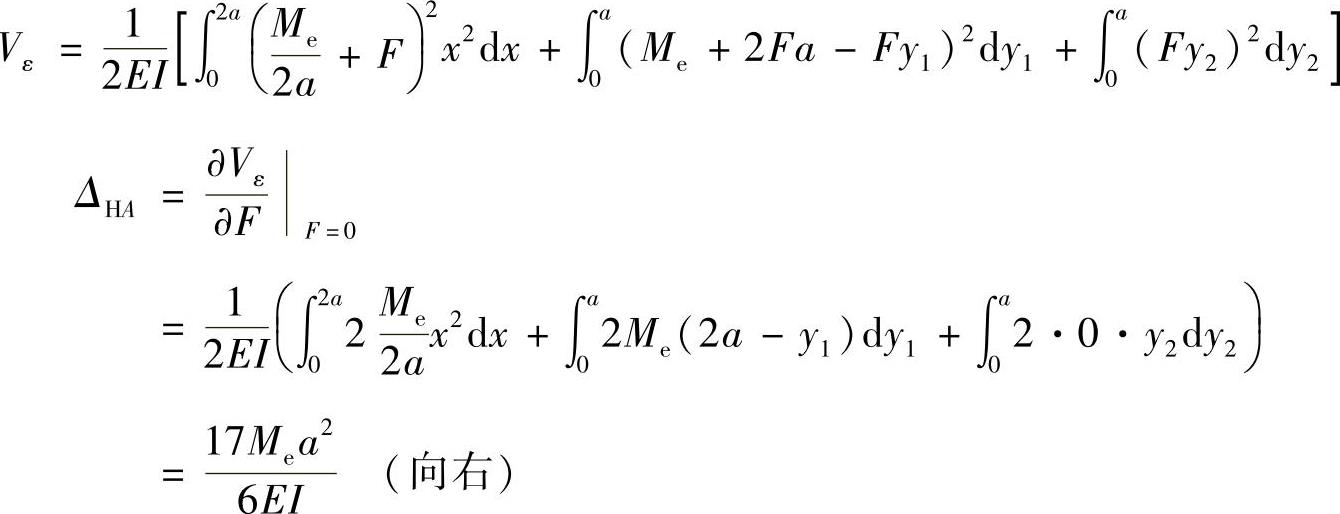
978-7-111-43425-2-Chapter12-39.jpg

（2）求截面A的转角θA。

截面A处添加一集中力偶矩MA，如图12-5b所示，刚架的应变能为

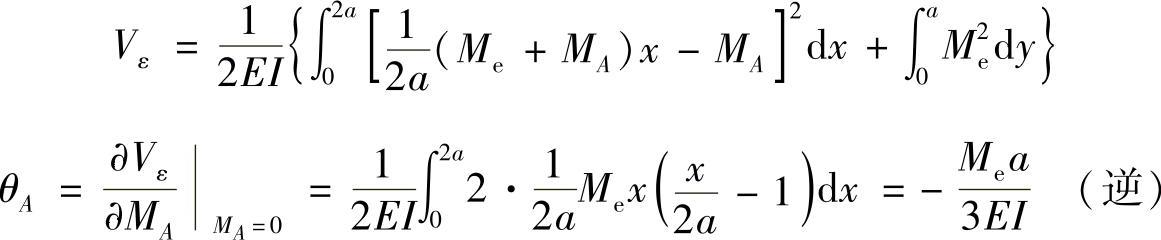
978-7-111-43425-2-Chapter12-40.jpg

（3）求截面B的转角θB。

截面B处添加力偶矩MB，如图12-5c所示，则刚架的应变能为

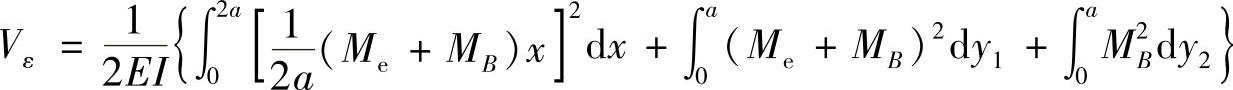
978-7-111-43425-2-Chapter12-41.jpg

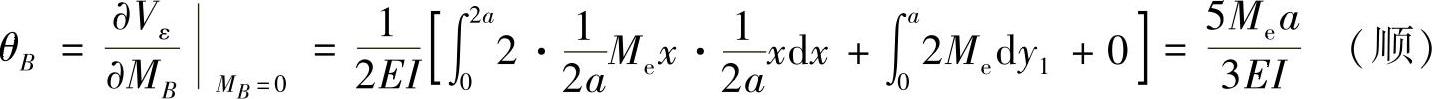
978-7-111-43425-2-Chapter12-42.jpg

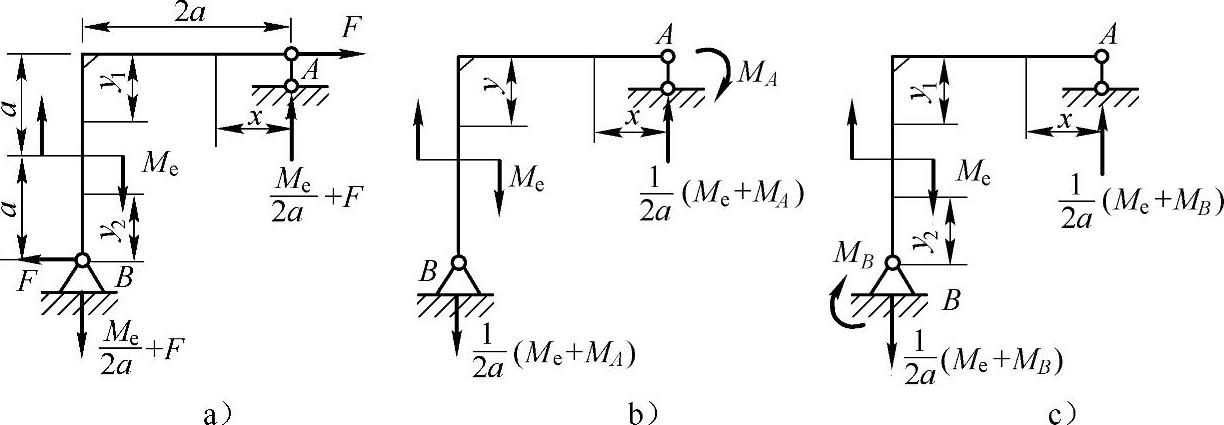
978-7-111-43425-2-Chapter12-43.jpg

图 12-5

图12-4b：

（1）求截面A的铅垂位移ΔVA。

截面A处添加一铅垂集中力F（图12-6a），刚架的应变能为

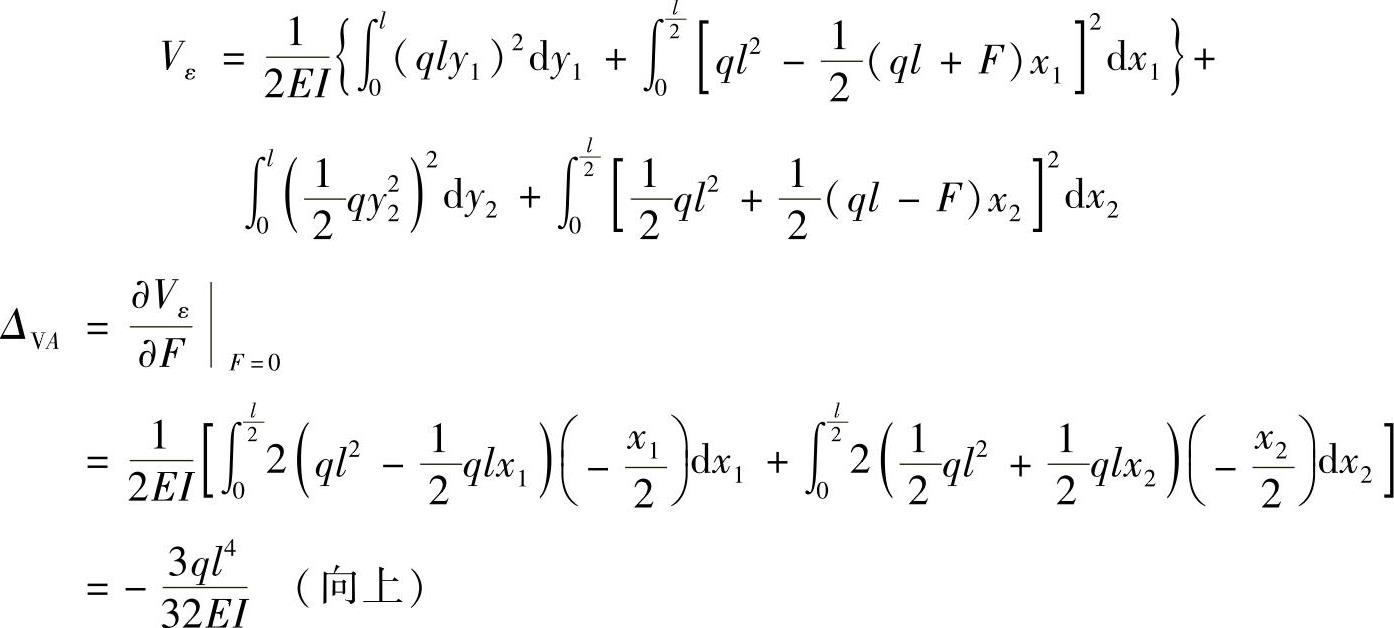
978-7-111-43425-2-Chapter12-44.jpg

（2）求截面A的水平位移ΔHA。

截面A处添加一水平集中力F（图12-6b），刚架的应变能为

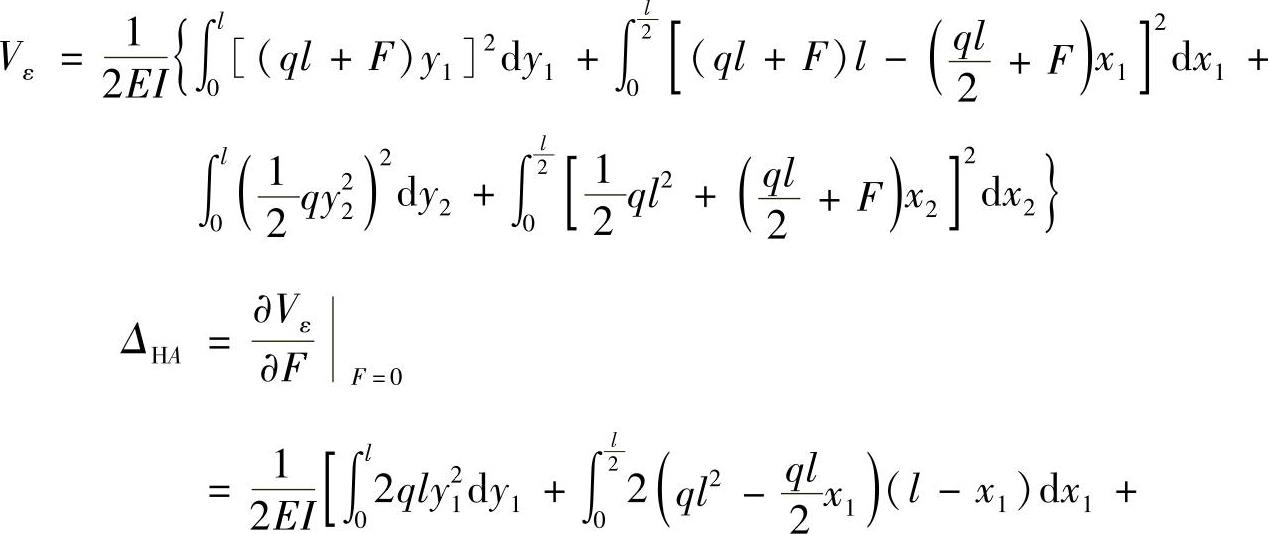
978-7-111-43425-2-Chapter12-45.jpg

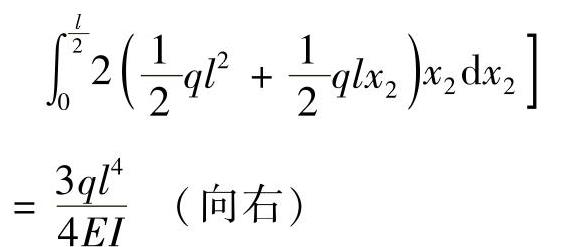
978-7-111-43425-2-Chapter12-46.jpg

（3）求截面A的转角θA。

在截面A处添加一集中力偶MA（图12-6c），刚架的应变能为

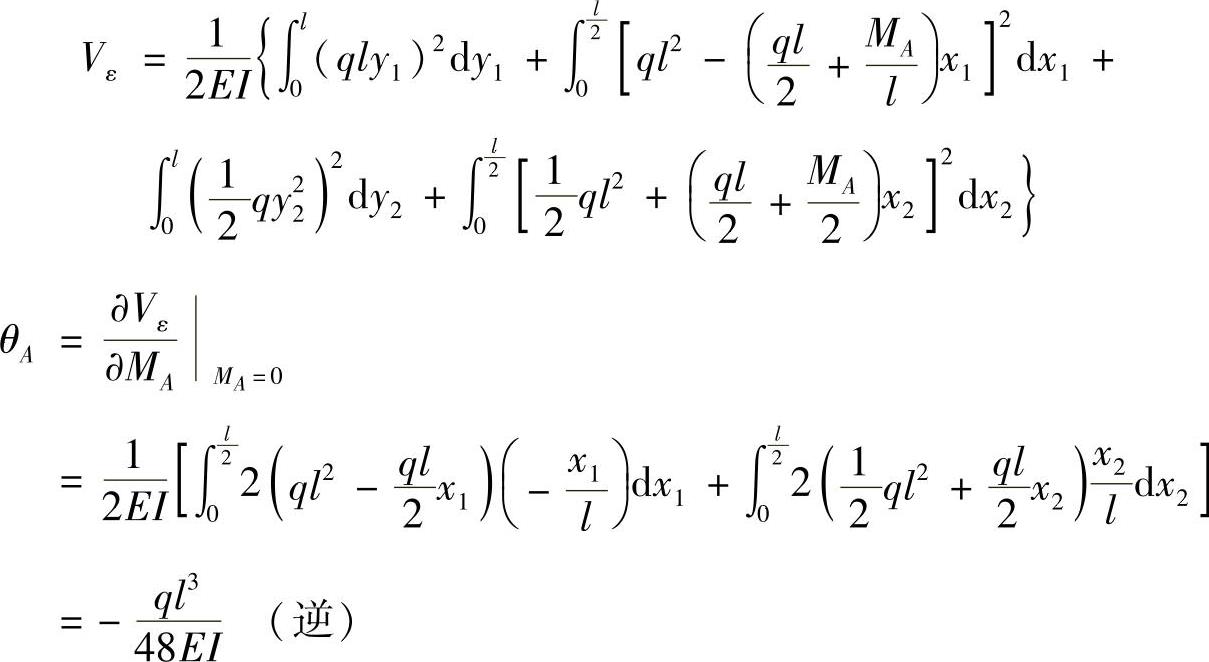
978-7-111-43425-2-Chapter12-47.jpg

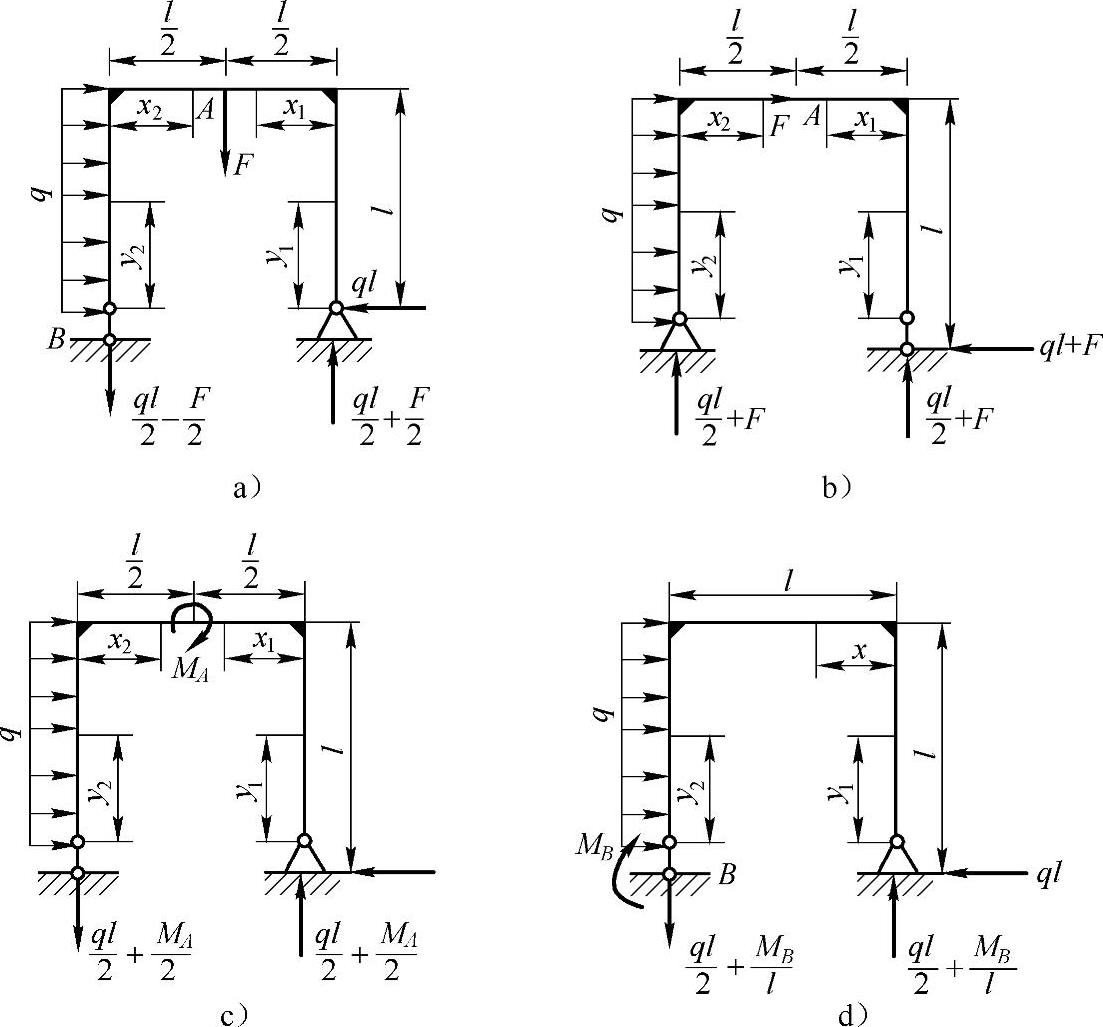
978-7-111-43425-2-Chapter12-48.jpg

图 12-6

（4）求截面B的转角θB。

截面B处添加一集中力偶MB（图12-6d），刚架的应变能为

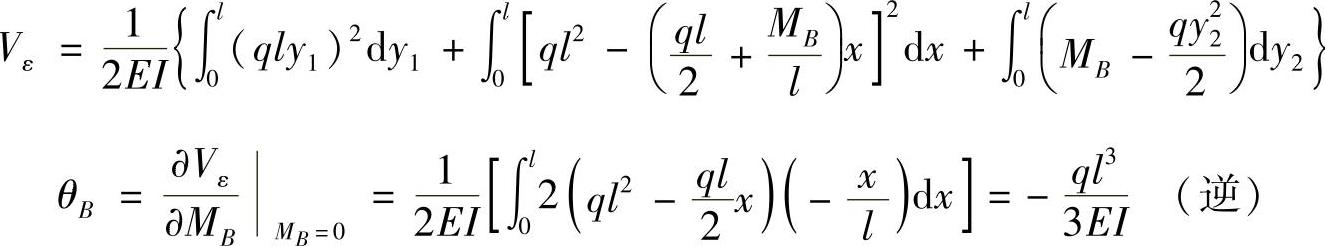
978-7-111-43425-2-Chapter12-49.jpg

图12-4c：

（1）截面A处的铅垂位移ΔVA。

令作用于A处的集中力F=F1，如图12-7a所示，则刚架的应变能为

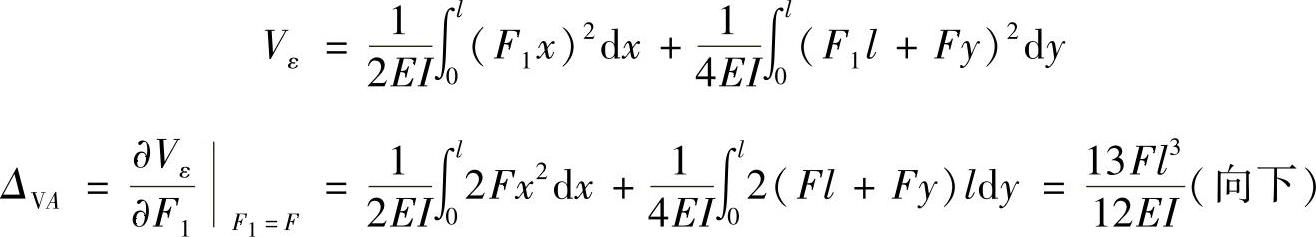
978-7-111-43425-2-Chapter12-50.jpg

（2）求截面A处的水平位移ΔHA。

令作用于截面B处的集中力F=F2，如图12-7b所示，则刚架的应变能为

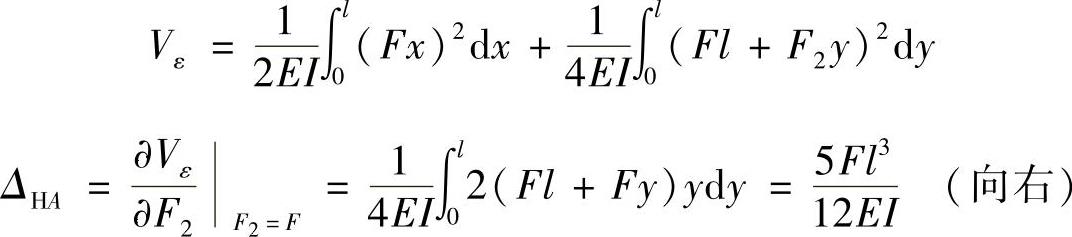
978-7-111-43425-2-Chapter12-51.jpg

（3）求截面A的转角θA。

在截面A处添加一力偶矩MA，如图12-7c所示，则刚架的应变能为

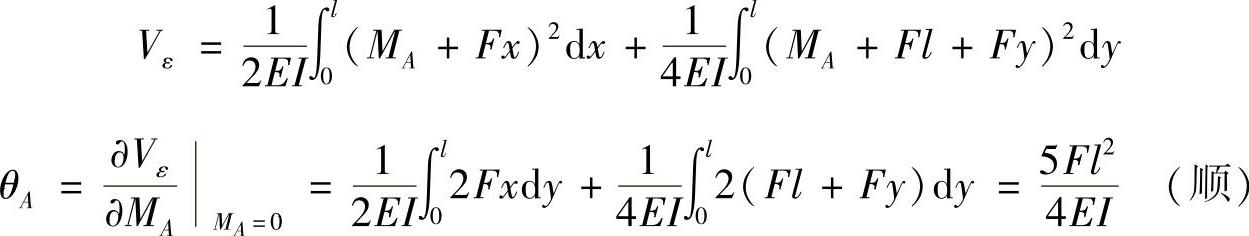
978-7-111-43425-2-Chapter12-52.jpg

（4）求截面B的转角θB。

在截面B处添加一力偶矩MB，如图12-7d所示，则刚架的应变能为

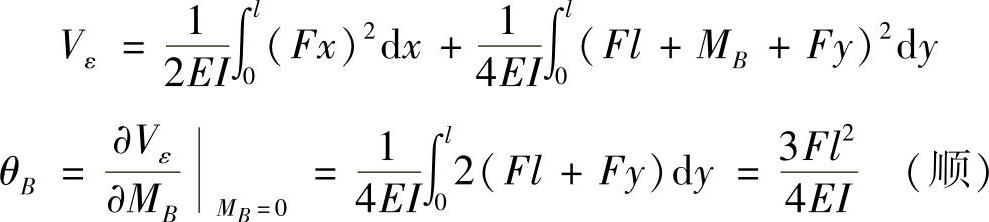
978-7-111-43425-2-Chapter12-53.jpg

图12-4d：

（1）求截面A处的水平位移ΔHA。

受力分析如图12-8a所示，则刚架的应变能为

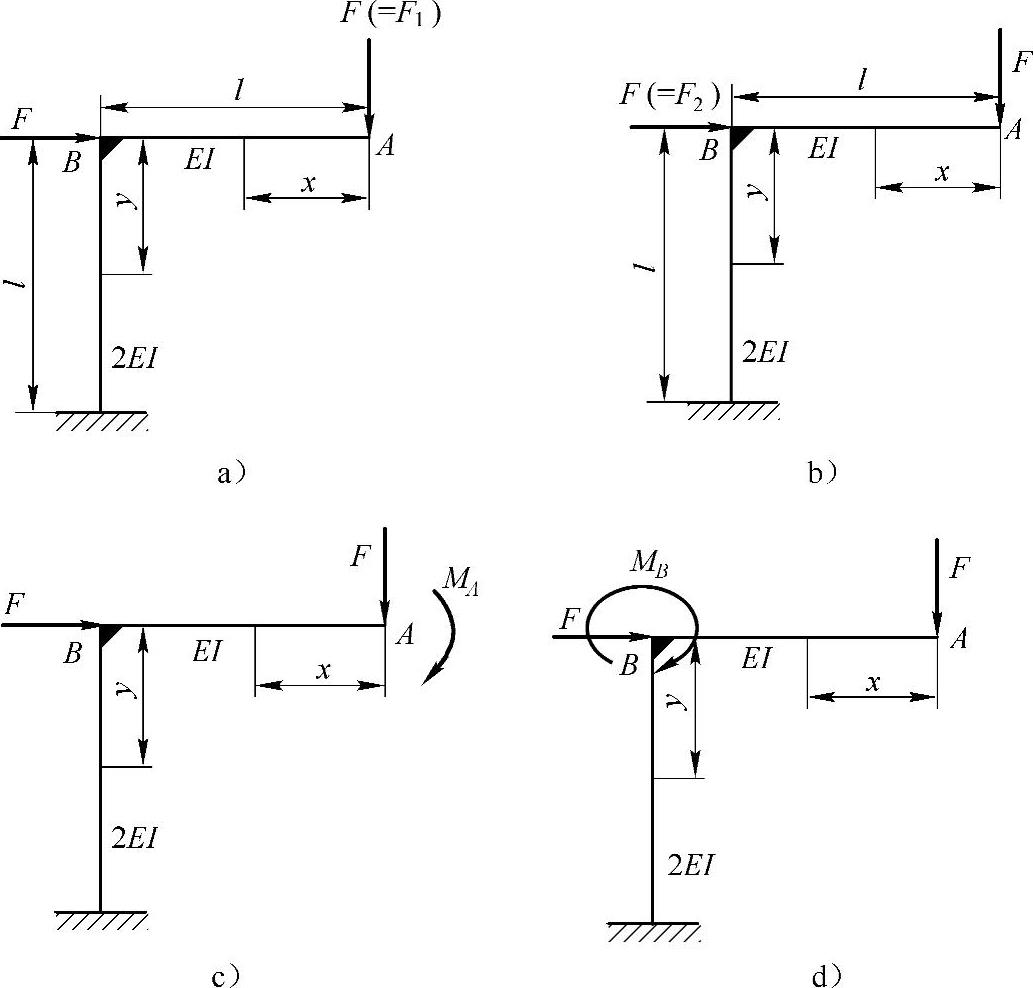
978-7-111-43425-2-Chapter12-54.jpg

图 12-7

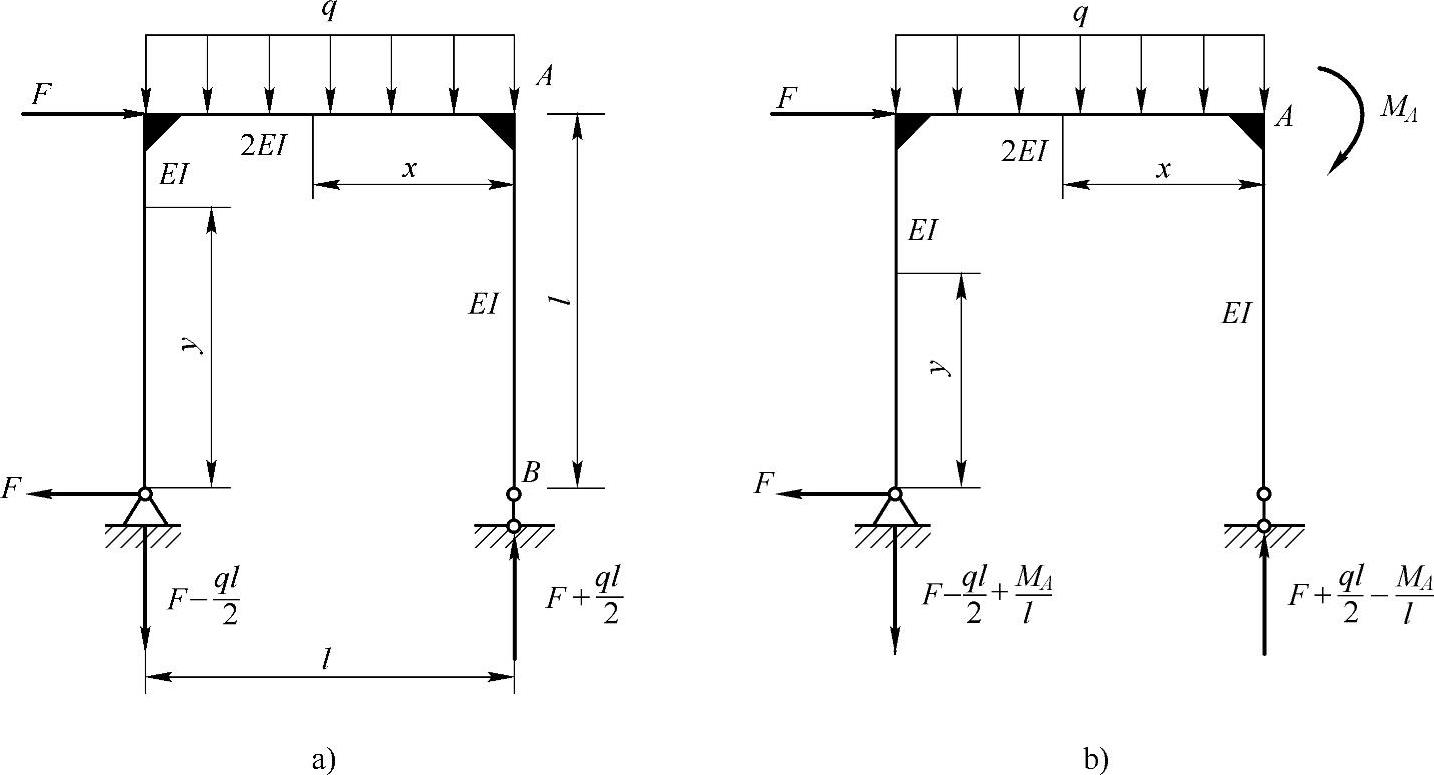
978-7-111-43425-2-Chapter12-55.jpg

图 12-8

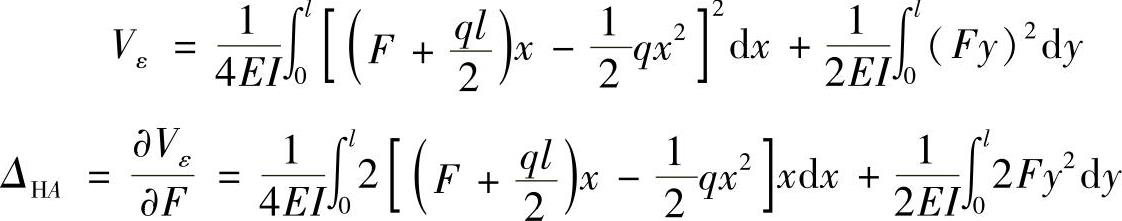
978-7-111-43425-2-Chapter12-56.jpg

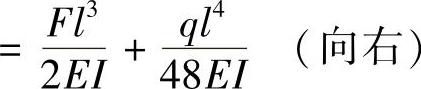
978-7-111-43425-2-Chapter12-57.jpg

（2）求截面A的转角θA。

在截面A处添加一力偶矩MA，如图12-8b所示，则刚架的应变能为

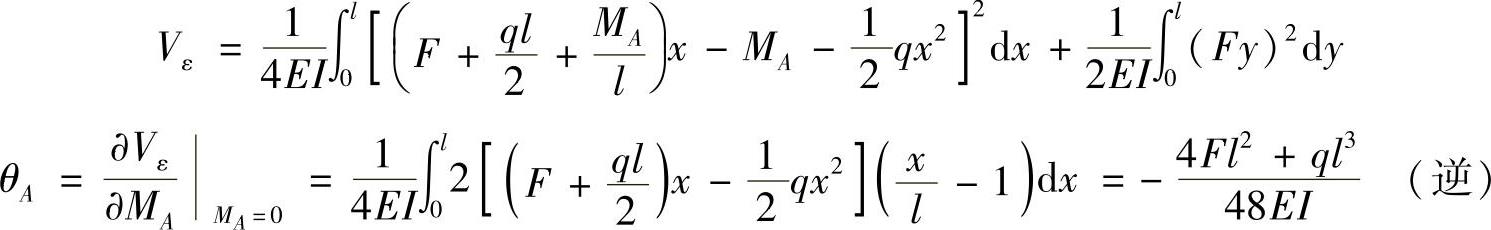
978-7-111-43425-2-Chapter12-58.jpg

（3）求截面B的转角θB。

因为刚架的AB段未承受横向力，所以AB段未发生弯曲变形，转角θB等于转角θA。

例12-5 已知图12-9a所示刚架各部分抗弯刚度均为EI，用单位载荷法计算B点水平位移、C点铅垂位移和C点转角。不计轴力对刚架变形的影响。

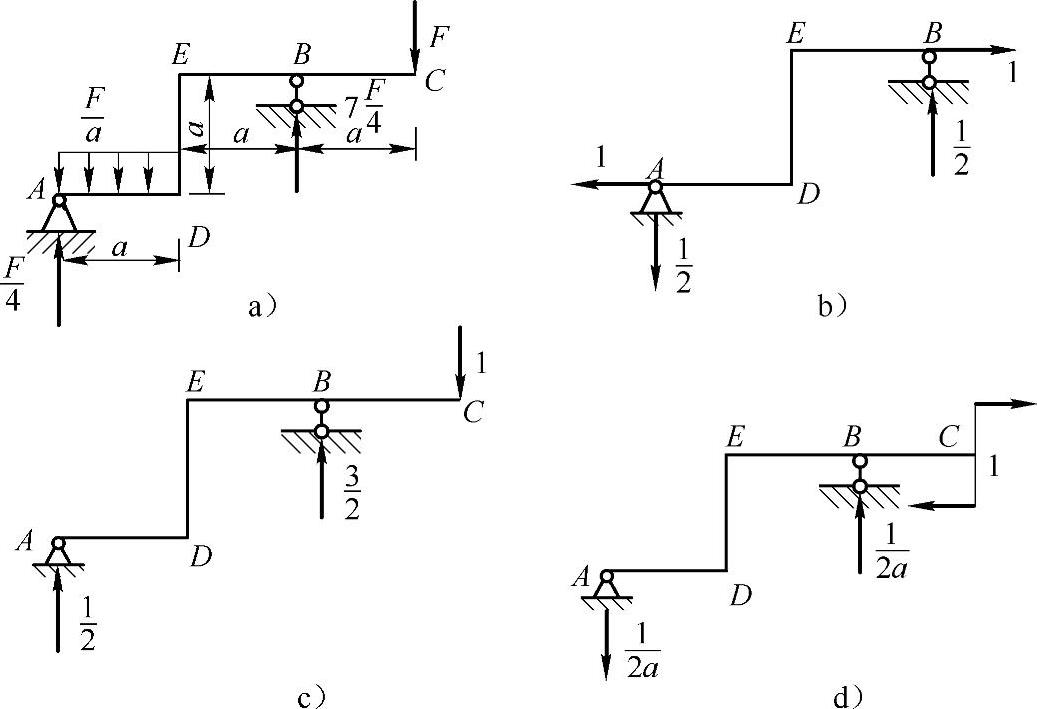
978-7-111-43425-2-Chapter12-59.jpg

图12-9 例12-5图

解：（1）写出各段弯矩方程。

在AD段，以A为原点，则

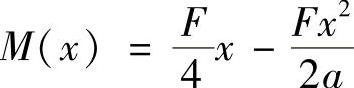
978-7-111-43425-2-Chapter12-60.jpg

在DE段，以D为原点，则

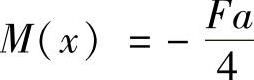
978-7-111-43425-2-Chapter12-61.jpg

在CB段，以C为原点，则

M（x）=-Fx

在BE段，以B为原点，则

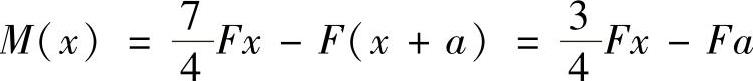
978-7-111-43425-2-Chapter12-62.jpg

（2）计算B点水平位移ΔB。

在B点加水平单位力，如图12-9b所示，则各段的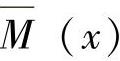978-7-111-43425-2-Chapter12-63.jpg为

在AD段，以A为原点，则 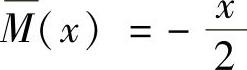978-7-111-43425-2-Chapter12-64.jpg

在DE段，以D为原点，则 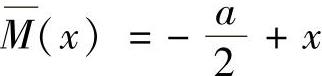978-7-111-43425-2-Chapter12-65.jpg

在CB段，以C为原点，则 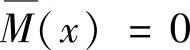978-7-111-43425-2-Chapter12-66.jpg

在BE段，以B为原点，则 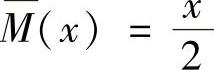978-7-111-43425-2-Chapter12-67.jpg

应用单位载荷法公式，得

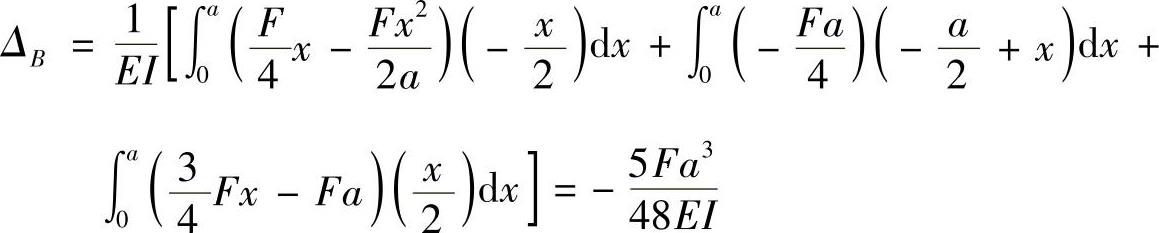
978-7-111-43425-2-Chapter12-68.jpg

其中，负号表示真实位移与所加单位力方向相反，即实际位移方向向左。

（3）计算C点铅垂位移ΔC。

在截面C加铅垂单位力，如图12-9c所示，则各段的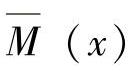978-7-111-43425-2-Chapter12-69.jpg为

在AD段，以A为原点，则 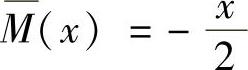978-7-111-43425-2-Chapter12-70.jpg

在DE段，以D为原点，则 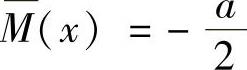978-7-111-43425-2-Chapter12-71.jpg

在CB段，以C为原点，则 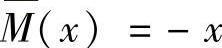978-7-111-43425-2-Chapter12-72.jpg

在BE段，以B为原点，则 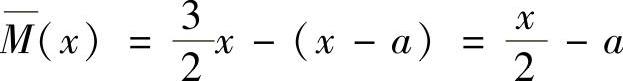978-7-111-43425-2-Chapter12-73.jpg

由此得

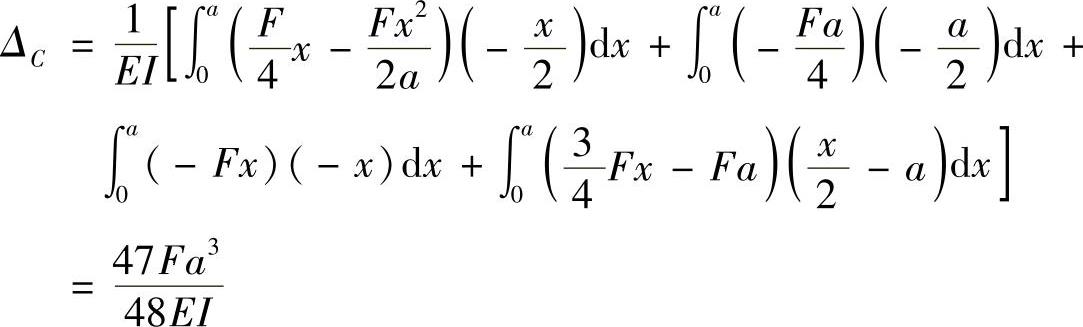
978-7-111-43425-2-Chapter12-74.jpg

（4）计算C点转角θC。

在C截面加单位力偶，如图12-9d所示，则各段的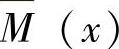978-7-111-43425-2-Chapter12-75.jpg为

在AD段，以A为原点，则 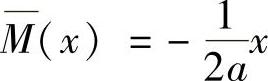978-7-111-43425-2-Chapter12-76.jpg

在DE段，以D为原点，则 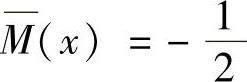978-7-111-43425-2-Chapter12-77.jpg

在CB段，以C为原点，则 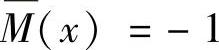978-7-111-43425-2-Chapter12-78.jpg

在BE段，以B为原点，则 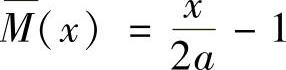978-7-111-43425-2-Chapter12-79.jpg

由此可得

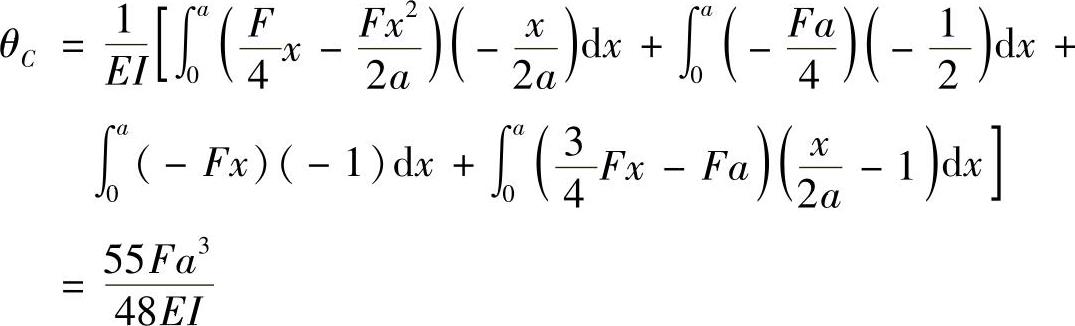
978-7-111-43425-2-Chapter12-80.jpg

例12-6 用单位载荷法求图12-10a所示曲杆A，B两点间的相对位移ΔAB。忽略轴力及剪力对曲杆变形的影响。

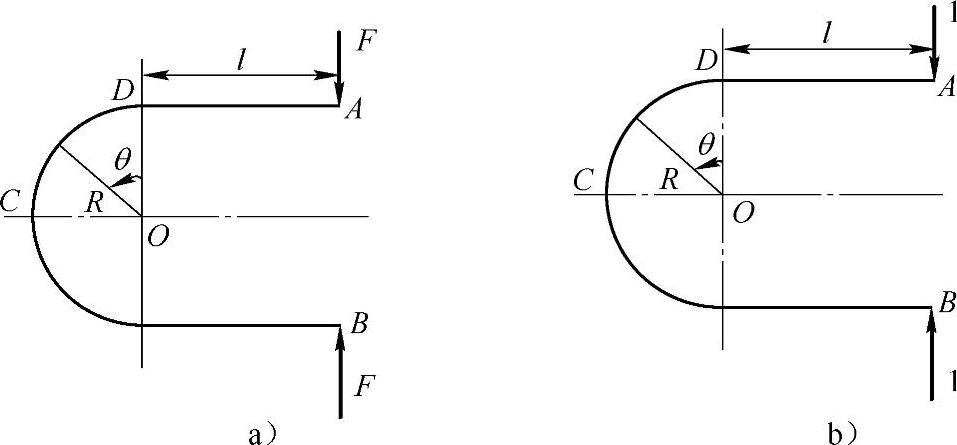
978-7-111-43425-2-Chapter12-81.jpg

图12-10 例12-6图

解：（1）列弯矩方程。

在AD段，以A为x轴的坐标原点，则

M（x）=Fx

在DC段，取极坐标如图12-10a所示，则

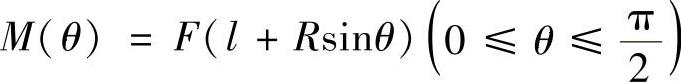
978-7-111-43425-2-Chapter12-82.jpg

（2）计算A，B两点间的相对位移ΔAB。

在A，B两点加单位力，如图12-10b所示则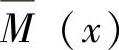978-7-111-43425-2-Chapter12-83.jpg为

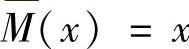
AD段： 978-7-111-43425-2-Chapter12-84.jpg

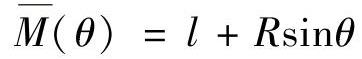
DC段： 978-7-111-43425-2-Chapter12-85.jpg

于是得

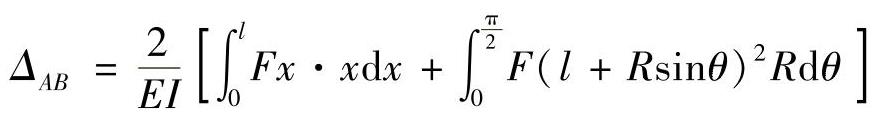
978-7-111-43425-2-Chapter12-86.jpg

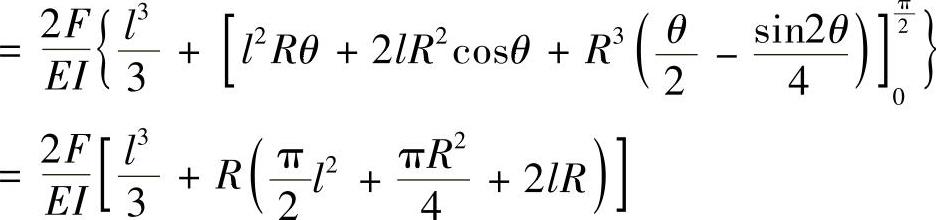
978-7-111-43425-2-Chapter12-87.jpg

例12-7 图12-11a所示为一水平放置的四分之一小曲率圆弧形曲杆。试计算在铅垂方向力F作用下，自由端B的铅垂位移。杆的EI和GIp均为已知。（不计剪力影响）

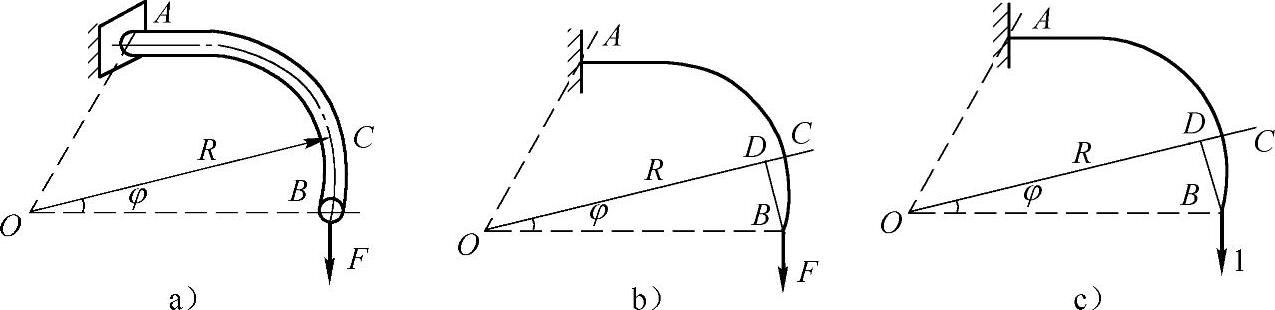
978-7-111-43425-2-Chapter12-88.jpg

图12-11 例12-7图

解：（1）写出弯矩方程和扭矩方程。

取图12-11b所示极坐标系，则有

弯矩方程 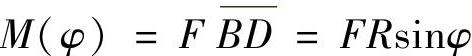978-7-111-43425-2-Chapter12-89.jpg

扭矩方程 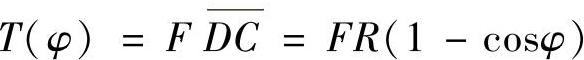978-7-111-43425-2-Chapter12-90.jpg

（2）计算B端铅垂位移。

在B处铅垂方向加单位力，如图12-11c所示，则

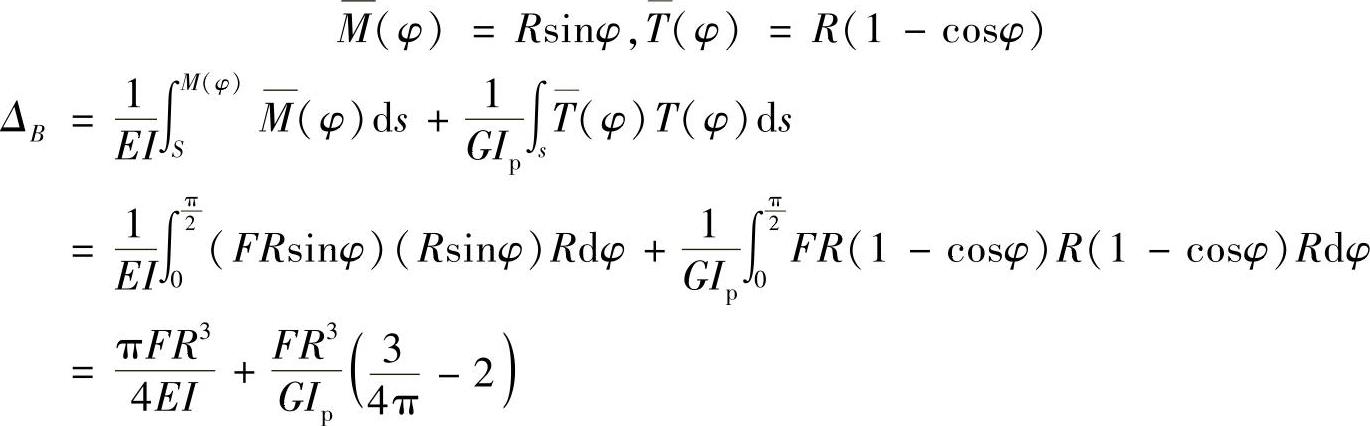
978-7-111-43425-2-Chapter12-91.jpg

例12-8 如图12-12所示长为l、直径为d的圆杆受一对横向压力F作用，求此杆长度的伸长量。已知E和μ。

解：由位移互等定理知：杆①的伸长量等于杆②直径的减少量。

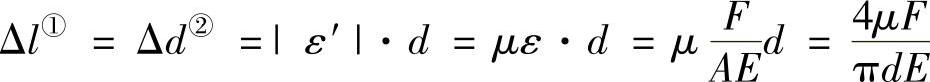
978-7-111-43425-2-Chapter12-92.jpg

例12-9 已知简支梁在均布载荷q作用下，梁的中点挠度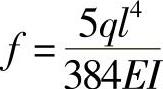978-7-111-43425-2-Chapter12-93.jpg（图12-13b）。求梁在中点集中力F作用下（图12-13a），梁的挠曲线与梁变形前的轴线所围成的面积ω。

解：根据功的互等定理，有

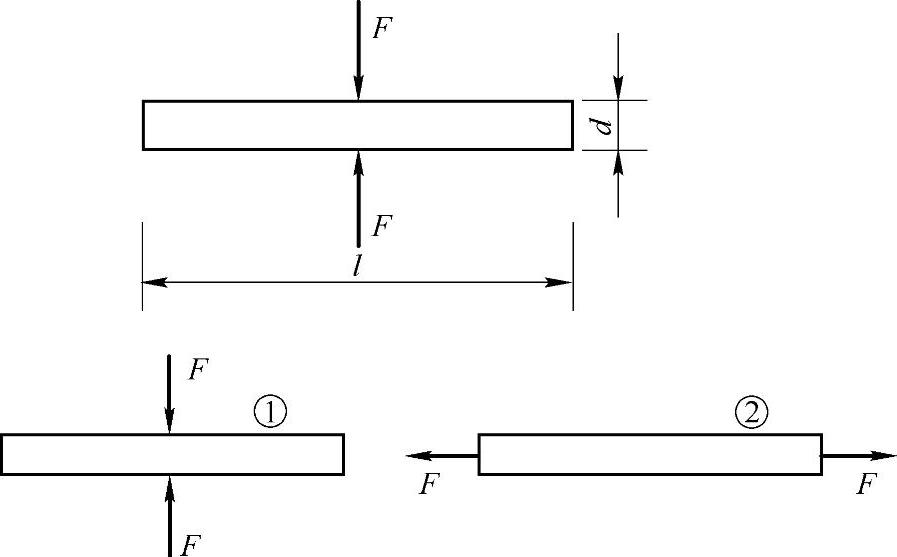
978-7-111-43425-2-Chapter12-94.jpg

图12-12 例12-8图

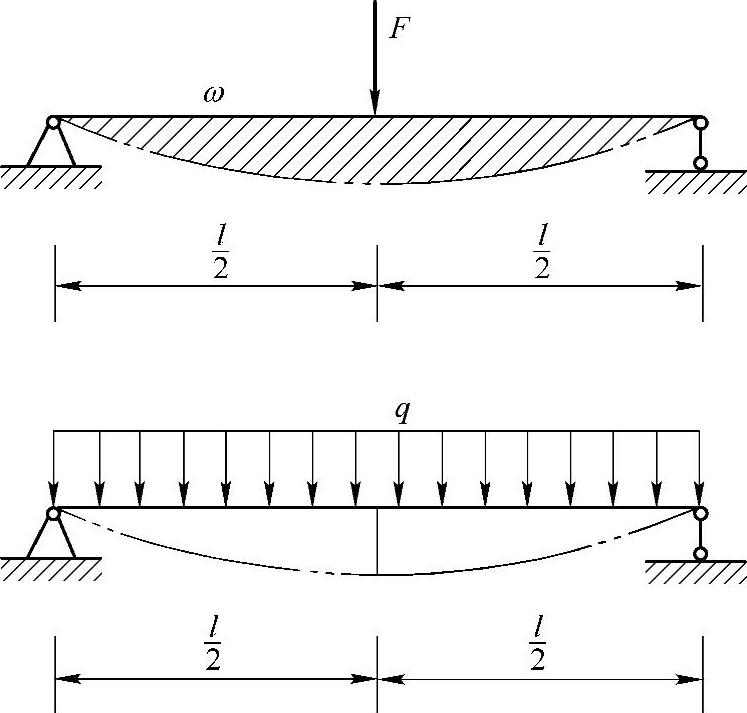
978-7-111-43425-2-Chapter12-95.jpg

图12-13 例12-9图

978-7-111-43425-2-Chapter12-96.jpg