7.4  习题

7.4 习题

习题7-1 微元受力如图7-14所示，图中应力单位为MPa。试根据不为零主应力的数目，它是（ ）。

（A）二向应力状态

（B）单向应力状态

（C）三向应力状态

（D）纯切应力状态

（参考答案：（B））

习题7-2 对于图7-15所示的应力状态（σ₁＞σ₂＞0），最大切应力作用面有以下四种，其中正确的是（ ）。

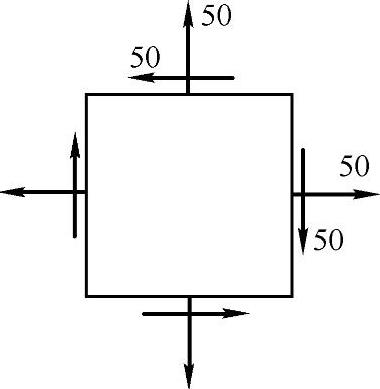
图7-14 习题7-1图

（A）平行于σ₂的面，其法线与σ₁夹45°角

（B）平行于σ₁的面，其法线与σ₂夹45°角

（C）垂直于σ₁和σ₂作用线组成平面的面，其法线与σ₁夹45°角

（D）垂直于σ₁和σ₂作用线组成平面的面，其法线与σ₂夹30°角

（参考答案：（A））

习题7-3 关于弹性体受力后某一方向的应力与应变的关系，有如下论述，其中正确的是（ ）。

（A）有应力一定有应变，有应变不一定有应力

（B）有应力不一定有应变，有应变一定有应力

（C）有应力不一定有应变，有应变不一定有应力

（D）有应力一定有应变，有应变不一定有应力

（参考答案：（A））

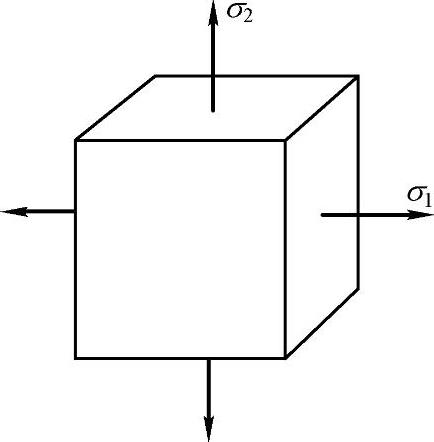
图7-15 习题7-2图

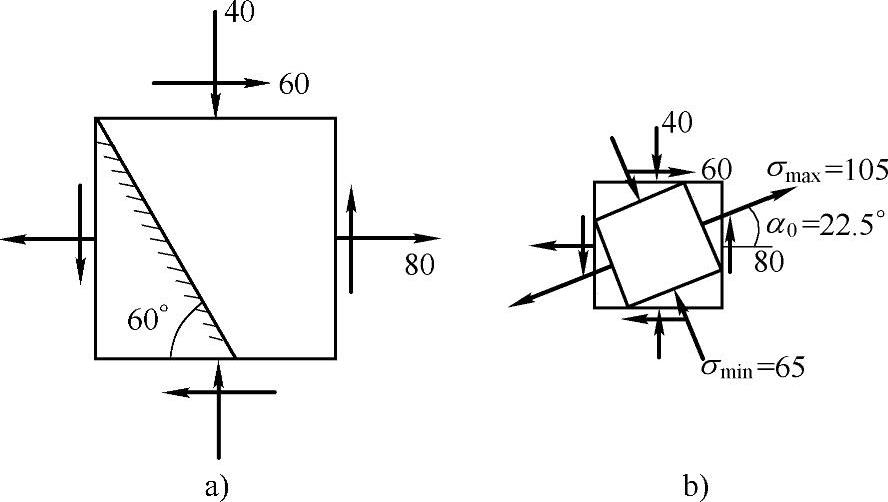
图7-16 习题7-4图

习题7-4 分别用解析法求图7-16a所示单元体的（1）指定斜截面上的正应力和切应力；（2）主应力值及主方向，并画在单元体上；（3）切应力最值。图中应力单位为MPa。（参考答案：（1）σ_α=102MPa，τ_α=22MPa；（2）σ₁=105MPa，σ₂=0，σ₃=-65MPa，α₀=22.5°或112.5°；（3）τ_max=85MPa，τ_min=-85MPa）

习题7-5 求图7-17所示应力状态的主应力和最大切应力（应力单位为Pa）。（参考答案：σ₁=130MPa，σ₂=30MPa，σ₃=-30MPa，τ_max=80MPa）

习题7-6 已知构件受力后其自由表面上一点处x方向的线应变ε_x=240×10^-6，y方向的线应变ε_y=-160×10^-6，试求该点处x和y截面上的正应力σ_x和σ_y，并求自由表面法线的线应变ε_z。已知材料的弹性模量E=210GPa，泊松比μ=0.3。（参考答案：ε_z=-34.3×10^-6）

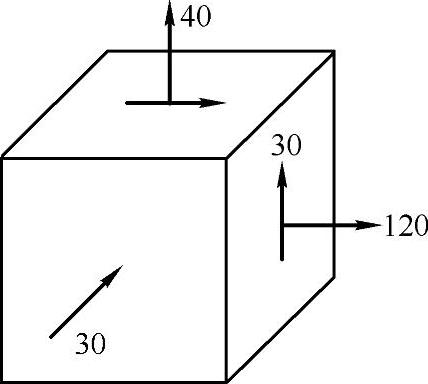
图7-17 习题7-5图

习题7-7 边长a=0.1m的铜质立方体置于刚性很大的钢块中的凹坑内（图7-18），钢块与凹坑之间无间隙。试求当铜块受均匀分布于顶面的竖向外加载荷F=300kN时，铜块内的主应力、最大切应力。已知铜的弹性模量E=100GPa，泊松比μ=0.34。铜块与钢块上凹坑之间的摩擦忽略不计。（参考答案：σ₁=σ₂=-15.5MPa，σ₃=-30MPa，τ_max=7.25MPa。）

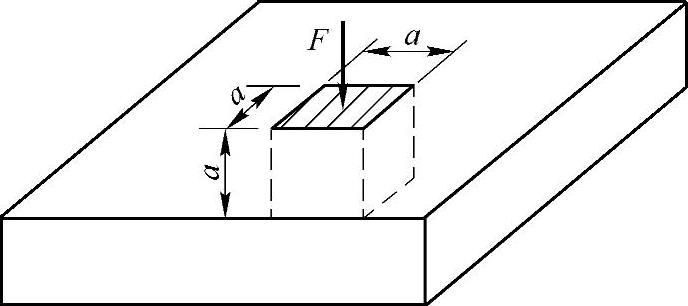
图7-18 习题7-7图

习题7-8 用Q235钢制成的实心圆截面杆，受轴向拉力F及扭转力偶矩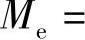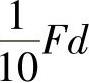作用。今测得圆杆表面k点处沿图7-19所示方向的线应变，ε=0.3。试求载荷F和M_e。若其许用应力[σ]=160MPa，试按第四强度理论校核杆的强度。（参考答案：F=2.01kN，M_e=2.01N·m，σ_r4=31.2MPa＜[σ]）

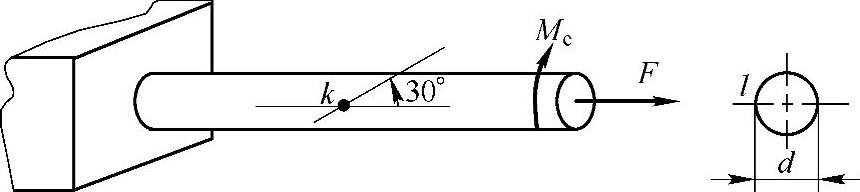
图7-19 习题7-8图