3.4  习题

3.4 习题

习题3-1 如图3-10所示阶梯形圆轴，AB段直径d₁=120mm，BC段直径d₂=100mm。外力偶矩M_A=20kN·m，M_B=34kN·m，M_C=14kN·m。材料的许用切应力[τ]=80MPa，切变模量G=80GPa，l₁=2m，l₂=1.5m，试校核该轴的强度，并计算截面C相对于截面A的扭转角φ_CA。（参考答案：τ_maxAB=59MPa，τ_maxBC=71.3MPa，φ_CA=0.125°）

习题3-2 如图3-11所示受扭转力偶作用的圆截面杆，长l=1m，直径d=20mm，材料的切变模量G=80GPa，两端截面的相对扭转角φ=0.1rad。试求此杆外表面任意处的切应变、横截面上的最大切应力和外力偶矩M。（参考答案：切应变λ=1×10^-3，τ_max=80MPa，M=125.6N·m）

习题3-3 一薄壁圆管如图3-12所示，两端承受力偶M_e的作用，使管产生扭转变形。已知圆管长l，管平均半径为R，横截面的上半圆壁厚为t₁，下半圆的壁厚为t₂，切变模量均为G。（1）试求扭转时横截面上的切应力；（2）试求圆管两端的相对扭转角。（参考答案：（1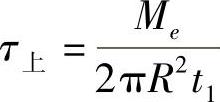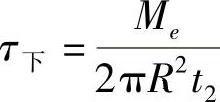），；（2）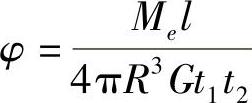

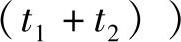
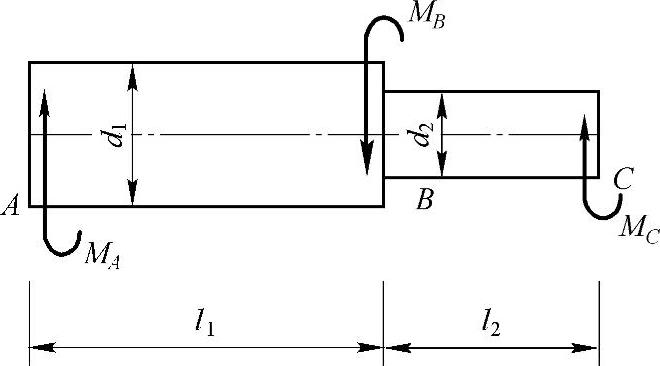
图3-10 习题3-1图

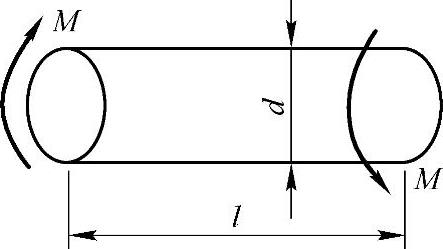
图3-11 习题3-2图

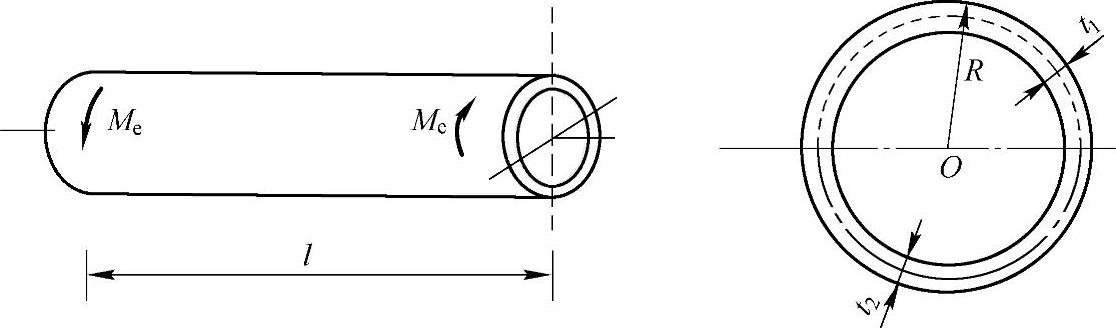
图3-12 习题3-3图

习题3-4 如图3-13所示三种截面形状（长宽比为2的矩形、正方形和圆形）的闭口薄壁杆，若截面中心线的长度、壁厚、材料和扭矩及杆长均相同，试计算三种截面上最大切应力之比和扭转角之比。（参考答案：τ_max，矩形∶τ_{max，正方形}∶τ_圆=1∶0.889∶0.698，θ_矩形∶θ_正方形∶θ_圆=1∶0.790∶0.487）

习题3-5 如图3-14所示T字形薄壁截面杆长为l=2m，材料的切变模量G=80GPa，受纯扭矩T=200N·m的作用，试求最大切应力及扭转角。（参考答案：τ_max=25MPa，φ=3.58°）

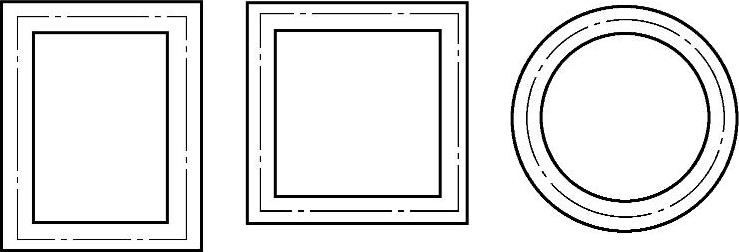
图3-13 习题3-4图

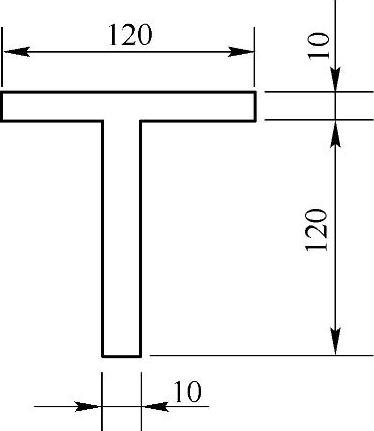
图3-14 习题3-5图

习题3-6 外径为120mm、厚度为5mm的薄壁圆杆，受T=4kN·m的扭矩作用，试按下列两种方式计算切应力。

（1）按闭口薄壁杆件扭转的近似理论计算；

（2）按空心圆截面杆扭转的精确理论计算。

（参考答案：（1）τ_max=38.5MPa；（2）τ_max=40.1MPa）

习题3-7 某桥式起重机，若其传动轴的转速为27r/min，传递功率为3kW，材料的许用扭转切应力[τ]=40MPa，切变模量G=80GPa，轴的许用单位长度扭转角[φ]=1（°）/m。试选择轴的直径。（参考答案：d=53mm）

习题3-8 某空心钢轴的外径D=100mm、内径d=50mm，若要求轴在2m内的最大扭转角不超过1.5°，问它所能承受的最大扭矩为多少？并求出此时轴内的最大切应力。已知材料的切变模量G=82GPa。（参考答案：最大扭矩T_max=9870N·m，最大切应力τ_max=53.6MPa）

习题3-9 如图3-15所示，阶梯形圆轴上装有三个带轮。已知各段轴的直径分别为d₁=38mm，d₂=75mm，主动轮B的输入功率P₃=32kW，从动轮A，C的输出功率分别为P₁=14kW，P₂=18kW；轴的额定转速n=240r/min，材料的许用扭转切应力[τ]=60MPa，切变模量G=80GPa，轴的许用单位长度扭转角[φ′]=1.8（°）/m，试校核该轴的强度和刚度。（参考答案：τ_ADmax=51.6MPa，τ_CBmax=15.3MPa，强度满足；φ_AD′=1.9（°）/m，φ′_CB=0.29（°）/m，不满足刚度要求）

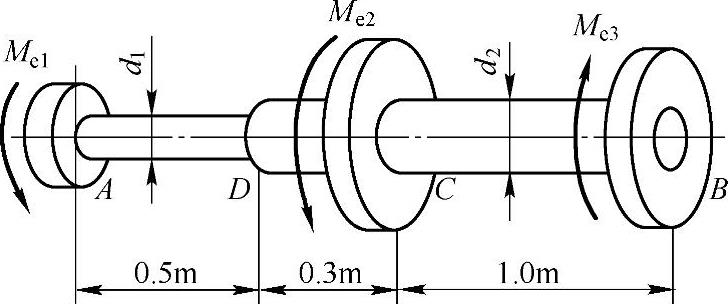
图3-15 习题3-9图

习题3-10 如图3-16所示，矩形截面钢杆受到扭转外力偶矩M_e=3kN·m的作用。已知材料的切变模量G=80GPa，试求：（1）杆内的最大切应力；（2）横截面短边中点处的切应力；（3）杆的单位长度扭转角。（参考答案：（1）τ_max=40.1MPa；（2）τ=34.4MPa；（3）φ′=0.564（°）/m）

习题3-11 空心钢轴的外径D=100mm，内径d=50mm，已知间距为l=2.7m的两横截面的相对扭转角φ=1.8°，材料的切变模量G=80GPa。试求：（1）轴内的最大切应力；（2）当轴以n=80r/min的速度旋转时，轴所传递的功率。（参考答案：（1）τ_max=46.5MPa；（2）P=71.8kW）

习题3-12 直径d=25mm的钢圆杆，受轴向力60kN作用时，在标距为200mm的长度内伸长了0.113mm。当其承受一对扭转外力偶矩M_e=0.2kN·m时，在标距为200mm的长度内相对扭转了0.732°的角度。试求钢材的弹性常数E，G和_μ。（参考答案：E=216GPa，G=81.6GPa，μ=0.324）

习题3-13 已知实心圆轴的转速n=300r/min，传递的功率P=330kW，轴材料的许用切应力[τ]=60MPa，切变模量G=80GPa。若要求在2m长度的相对扭转角不超过1°，试求该轴的直径。（参考答案：d≥111mm）

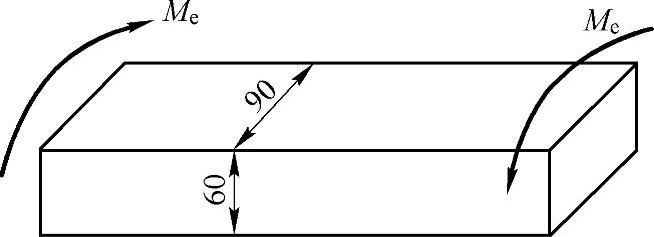
图3-16 习题3-10图

习题3-14 有一壁厚为25mm、内径为250mm的空心薄壁圆管，其长度为1m，作用在轴两端面内的外力偶矩为180kN·m。试确定管中的最大切应力，并求管内的应变能。已知材料的切变模量G=80GPa。（参考答案：τ_max=65.5MPa，V_ε=492N·m）

习题3-15 图3-17所示为薄壁杆的两种不同形状的横截面，其壁厚及管壁中线的周长均相同。两杆的长度和材料也相同，当在两端承受相同的一对扭转外力偶矩时，试求：（1）最大切应力之比；（2）相对扭转角之比。（参考答案：（1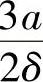），（2））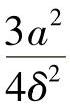

习题3-16 有一外径为100mm、内径为80mm的空心圆轴，与一直径为80mm的实心圆轴用键相联结，如图3-18所示。在A轮处由电动机带动，输入功率P₁=150kW，在B，C两轮处分别负载P₂=75kW，P₃=75kW。若已知轴的转速为n=300r/min，许用切应力[τ]=45MPa；键的尺寸为10mm×10mm×30mm，其许用应力[τ]=100MPa和[σ_bs]=280MPa。（1）作扭矩图；（2）校核空心轴及实心轴的强度（不考虑键槽的影响）；（3）求所需键数n。（参考答案：（1）T₁=4.78kN·m，T₂=2.39kN·m，T₃=2.39kN·m；（2）AB段：τ_max=41.2MPa，BC段：τ_max=23.8MPa，强度满足要求；（3）n=2）

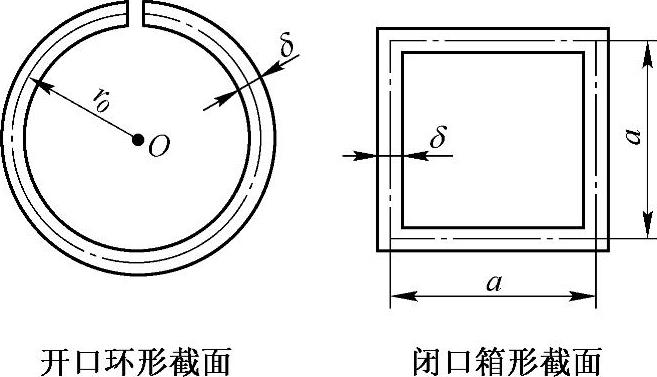
图3-17 习题3-15图

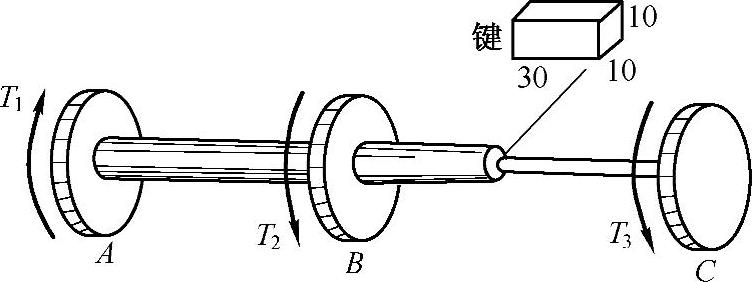
图3-18 习题3-16图

习题3-17 圆轴受力如图3-19所示，已知：D=30mm，d=15mm，[τ]=50MPa，[φ]=2.5（°）/m，G=80GPa，试对此轴进行强度和刚度校核。（参考答案：BC段：τ_max=49.9MPa，DE段：τ_max=47.5MPa，强度满足要求；BC段：φ_max=2.38（°）/m，DE段：φ_max=2.27（°）/m，刚度满足要求）

习题3-18 一矩形截面杆，截面尺寸h×b=90mm×60mm，承受的扭矩为3.5kN·m。试计算杆内的最大切应力。如果改为截面面积相等的圆截面杆，再计算杆内的最大切应力，并比较两者的大小。（参考答案：矩形截面τ_max1=46.8MPa，圆形截面τ_max2=31.2MPa）

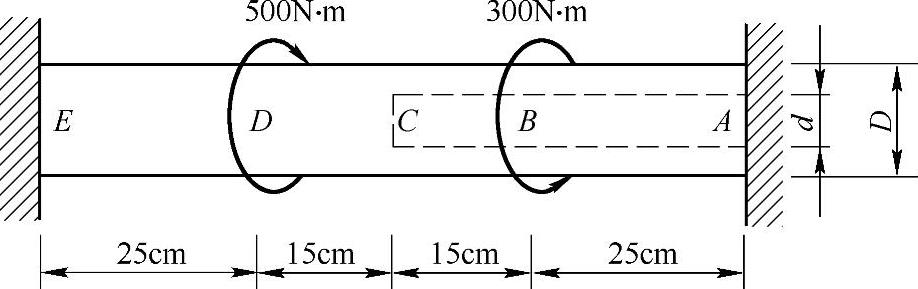
图3-19 习题3-17图

习题3-19 一矩形截面等直钢杆，其横截面尺寸h×b=100mm×50mm，长度l=2m，在杆的两端受到一对矩为M_e=4kN·m的外力偶的作用。已知钢的许用扭转切应力[τ]=100MPa，切变模量G=80GPa；轴的许用单位长度扭转角[φ′]=1（°）/m。试校核该杆的强度和刚度。（参考答案：τ_max=65.0MPa，φ′=1.0（°）/m）

习题3-20 簧杆直径d=18mm的圆柱形密圈螺旋弹簧，受拉力F=0.5kN作用，弹簧的平均直径为D=125mm，材料的切变模量G=80GPa。试求：（1）簧杆内的最大切应力；（2）为使其伸长量等于6mm所需的弹簧有效圈数。（参考答案：（1）τ_max=32.8MPa；（2）n=6.4圈）