11.3  例题解析

11.3 例题解析

例11-1 一点交变应力的循环曲线如图11-5所示，确定该交变应力的最大应力σ_max、最小应力σ_min，应力幅σ_a、平均应力σ_m和循环特征r。

解：由图示特性曲线可得最大应力和最小应力分别为

σ_max =30MPa，σ_min=-60MPa

所以应力幅和平均应力分别为

σ_a =45MPa，σ_m=-15MPa

则循环特征为

r=-2

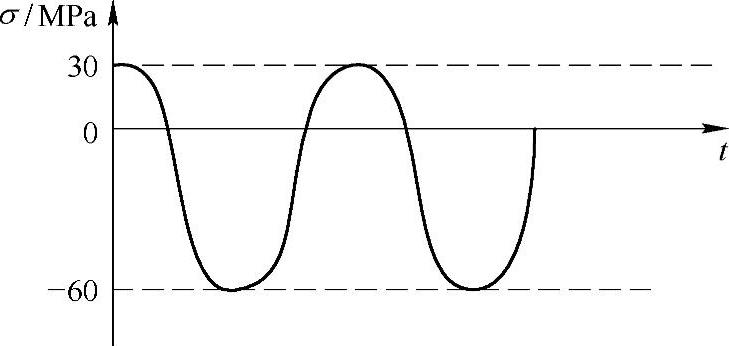
图11-5 例11-1图

例11-2 试计算图11-6所示各交变应力的循环特征和应力幅。

解：（a）循环特征为

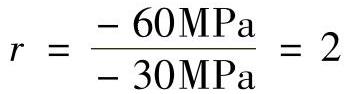
应力幅为

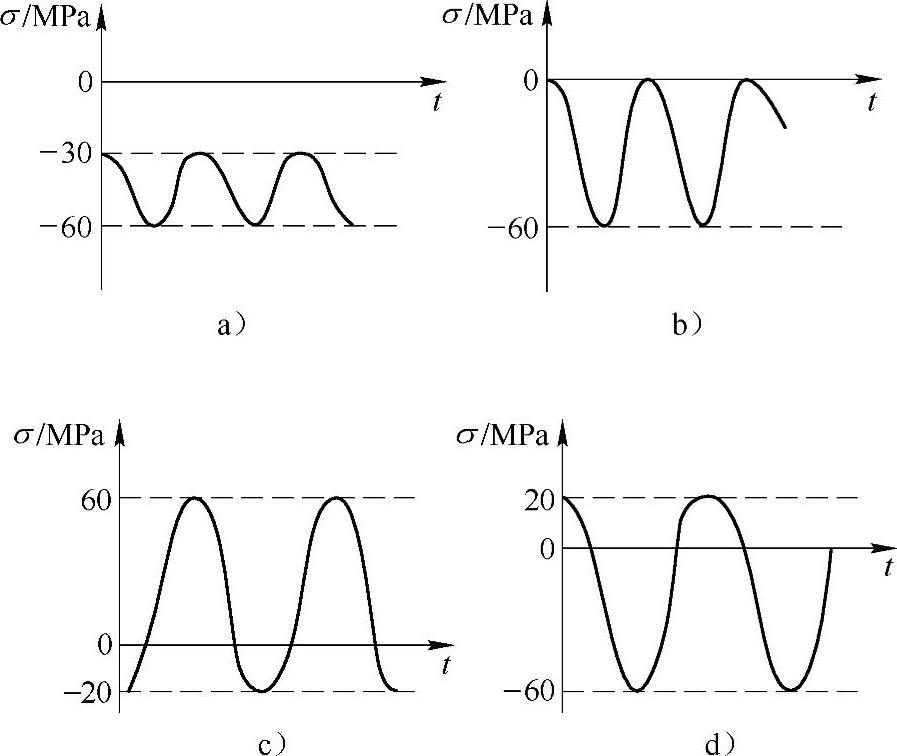
图11-6 例11-2图

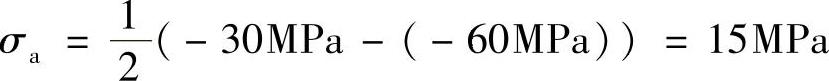
（b）循环特征为

r=-∞

应力幅为

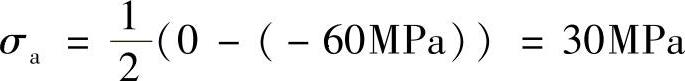
（c）循环特征为

应力幅为

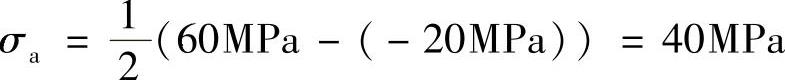
（d）循环特征为

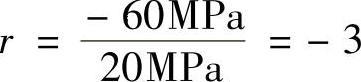
应力幅为

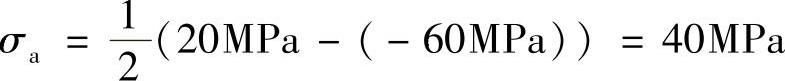
例11-3 图11-7a所示为直径d=30mm的钢圆轴，受横向力F₂=0.2kN和轴向拉力F₁=5kN的联合作用。当轴以匀角速ω转动时，试绘出跨中截面上k点处的正应力随时间变化的曲线，并计算其循环特征和应力幅。

解：跨中截面上k点处的正应力为

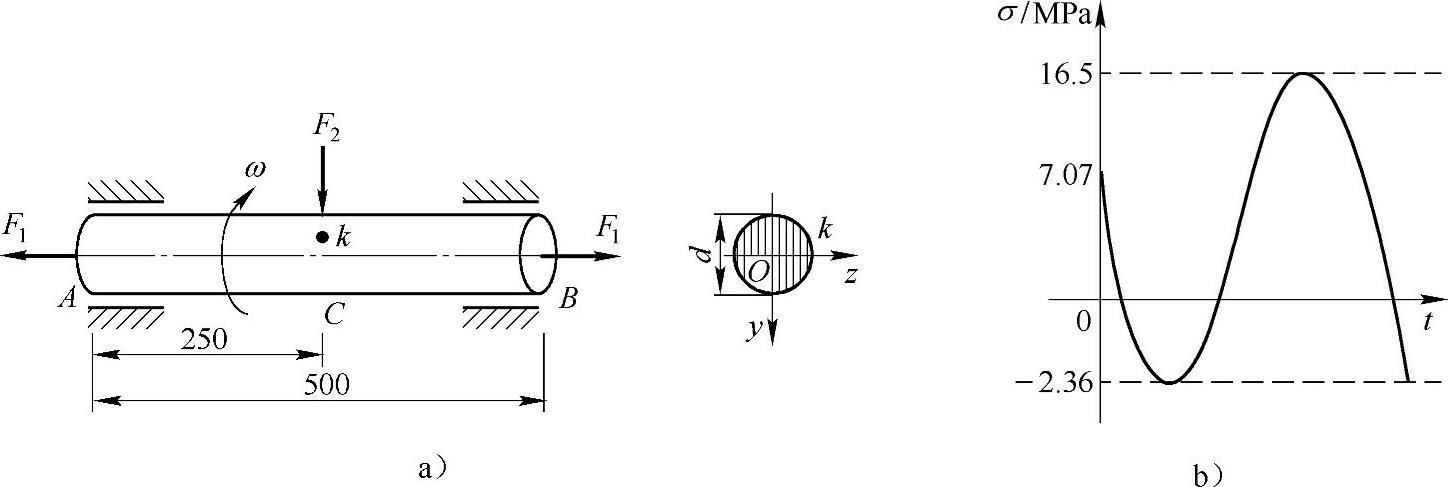
图11-7 例11-3图

跨中截面上k点处的正应力随时间变化曲线如图11-7b所示。

其循环特征

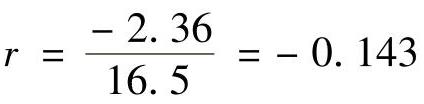
应力幅为

Δσ=[16.5-（-2.36）]MPa=18.86MPa