5.3  例题解析

5.3 例题解析

例5-1 图5-4所示桥式起重机大梁上小车的每个轮子对大梁的压力均为F，小车的轮距为d，大梁的跨度为l。试问小车在什么位置时梁内的弯矩最大？其最大弯矩值等于多少？最大弯矩在何截面？

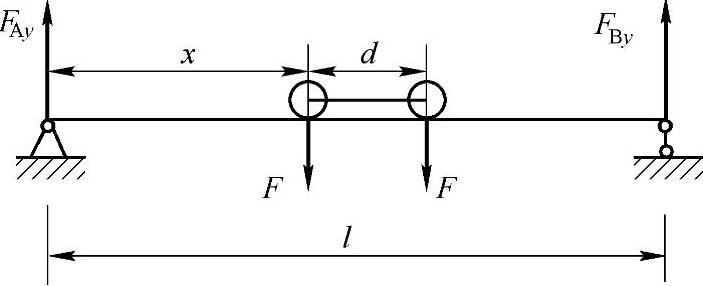
图5-4 例5-1图

解：求支座约束力，作内力图如图5-4所示。

当小车的左轮运动到距梁左端A任意x位置时，由ΣM_A=0得

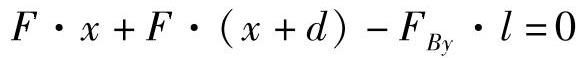
即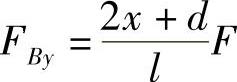

由ΣF_y=0得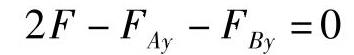

即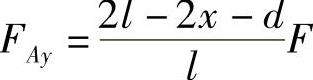

则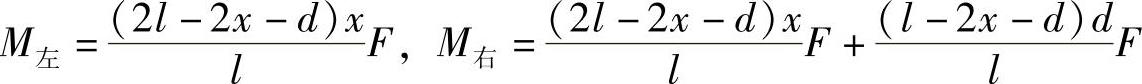

下面求最大弯矩及其所在截面和小车的位置：

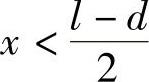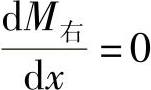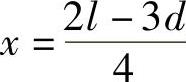当l-2x-d＞0时，即时，小车右轮所在截面上的弯矩为最大弯矩，即M_右=M_max，令，得，此时

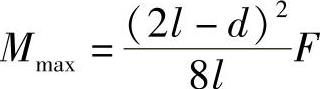
当l-2x-d＜0时，即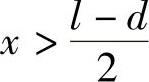时，小车左轮所在截面上的弯矩为最大弯矩，

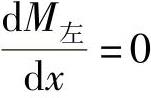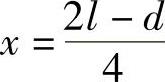即M_左=M_max，令，得，此时

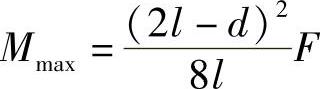
其中，弯矩图如图5-5所示。

例5-2 长度l=250mm、截面宽度b=25mm、高度h=0.8mm的薄钢尺，由于两端外力偶矩的作用而弯成中心角为60°的圆弧。已知钢的弹性模量E=210GPa，试求钢尺横截面上的最大正应力。

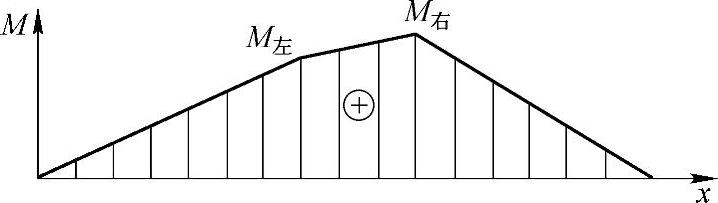
图5-5 弯矩图

解：根据题意 ，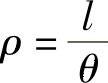

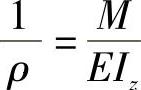
可以得到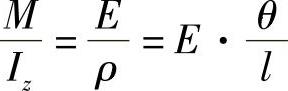

故钢尺横截面上的最大正应力为

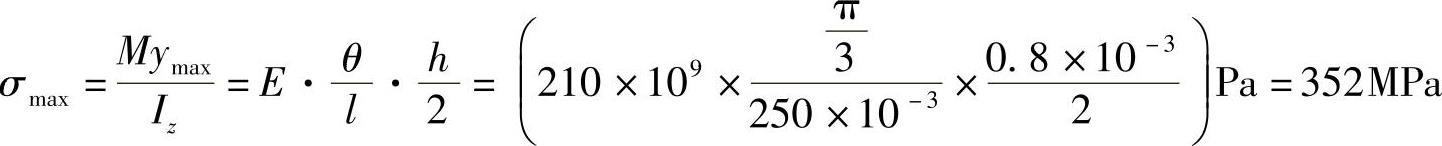
例5-3 图5-6所示为矩形截面简支梁。试求1—1截面上a，b两点的正应力和切应力。

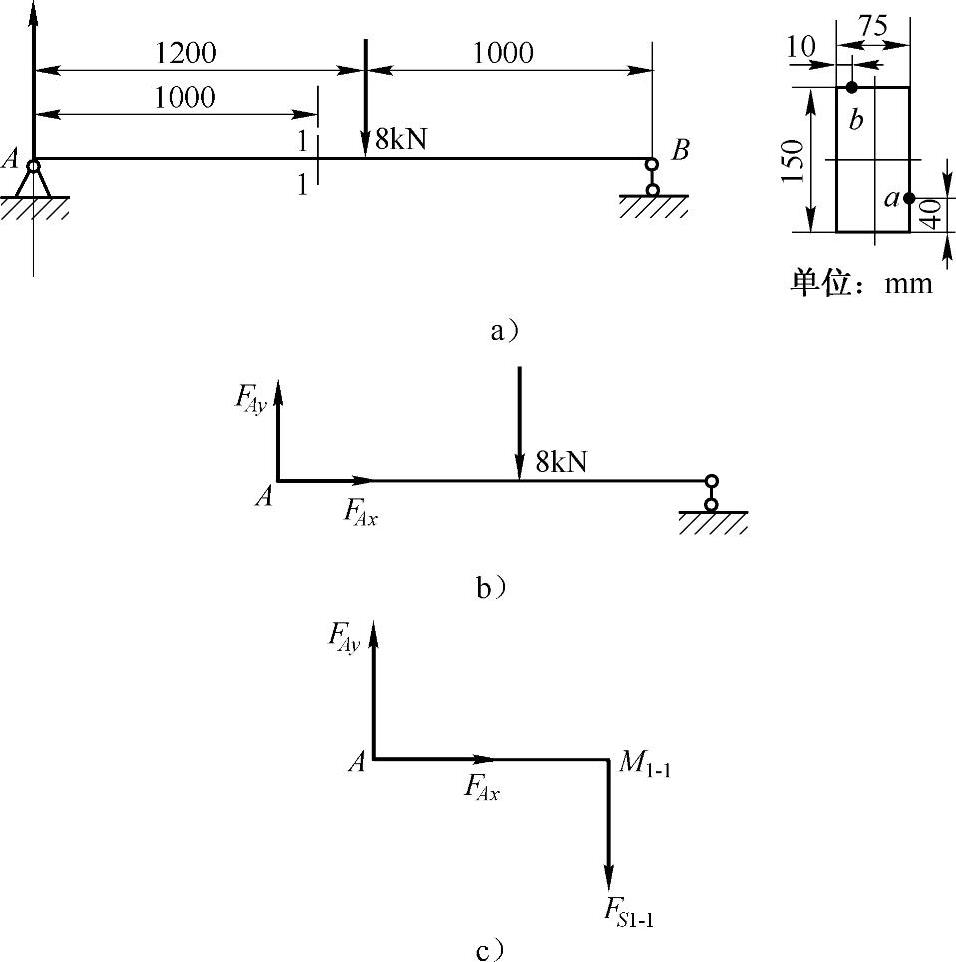
图5-6 例5-3图

解：（1）求1—1截面上的剪力和弯矩。先求支座A处的支反力，如图5-6b所示，有

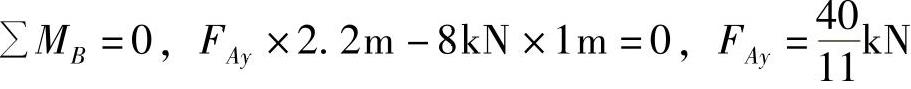
再列图5-6c所示的平衡方程，有

ΣF_y=0，F_Ay-F_S1-1=0

ΣM_A=0，F_S1-1×1m-M_1-1=0

所以1—1截面上的剪力和弯矩分别为

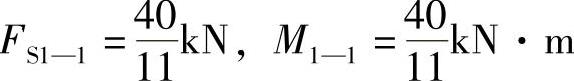
（2）求1—1截面上a，b两点的应力。

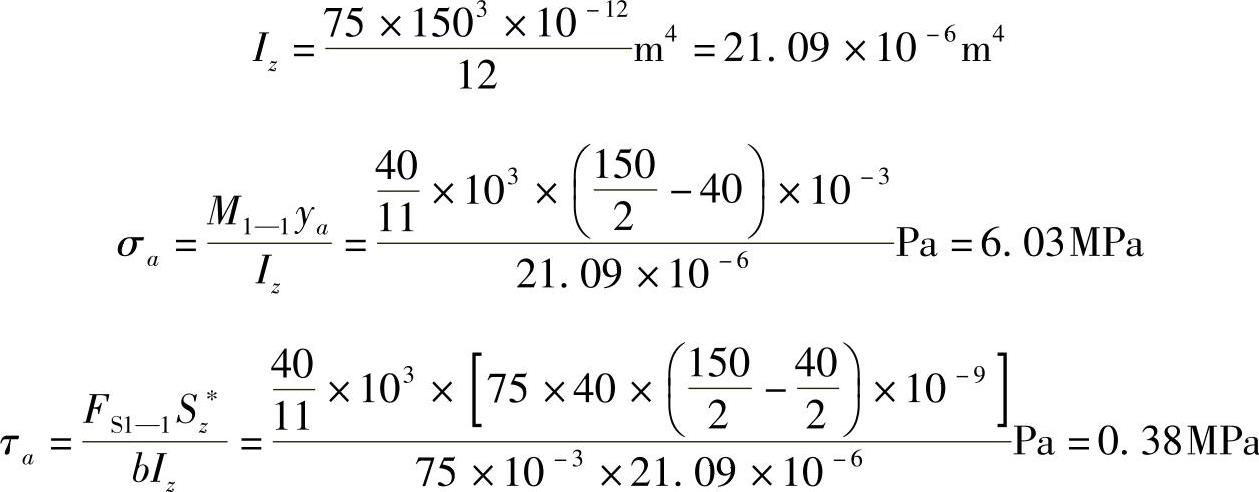
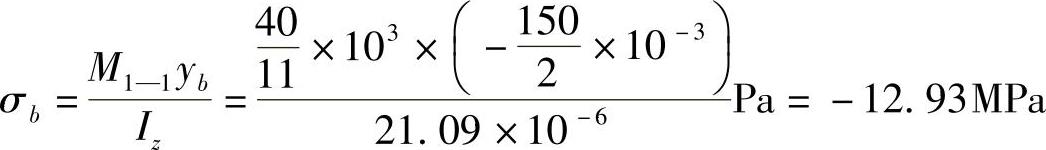
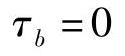
例5-4 如图5-7所示钢油管外径D=762mm，壁厚t=9mm，油的密度ρ₁=8.46×10²kg/m³，钢的密度ρ₂=7.76×10³kg/m³，钢管的许用正应力[σ]=170MPa。若将油管简支在支墩上，试求允许的最大跨长l。

解：（1）作油管的受力简图。

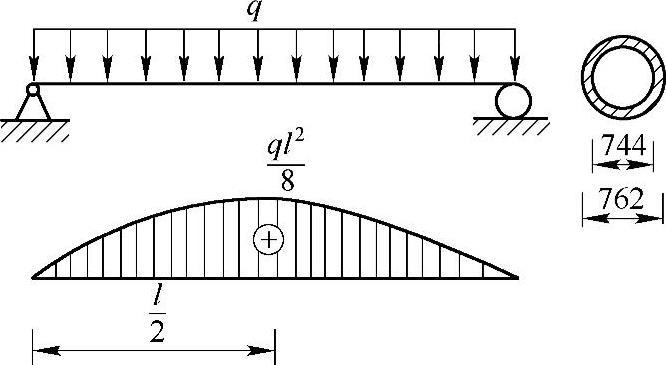
图5-7 例5-4图

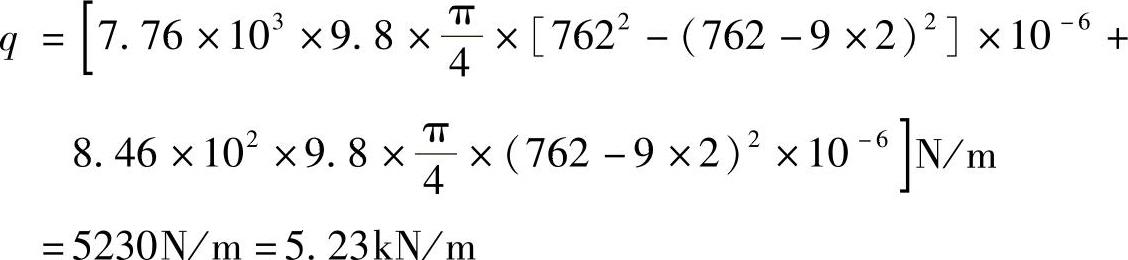
（2）求允许的最大跨长l。

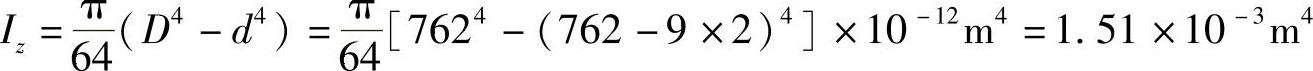
由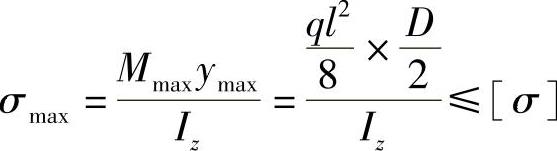，得到

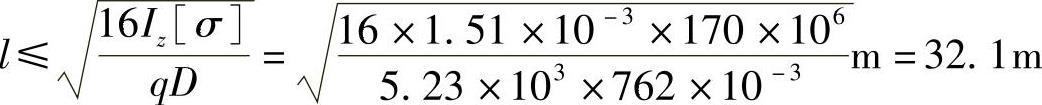
所以允许的最大跨长为32.1m。

例5-5 图5-8所示正方形截面悬臂木梁承受载荷作用。已知木材的许用正应力[σ]=10MPa。现需要在梁的C截面中性轴处钻一直径为d的圆孔，试问在保证该梁强度的条件下，圆孔的最大直径d可达多少（不考虑圆孔处应力集中的影响）？

解：C截面为危险截面。

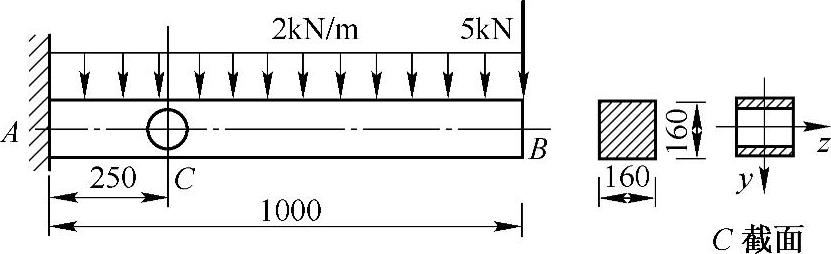
图5-8 例5-5图

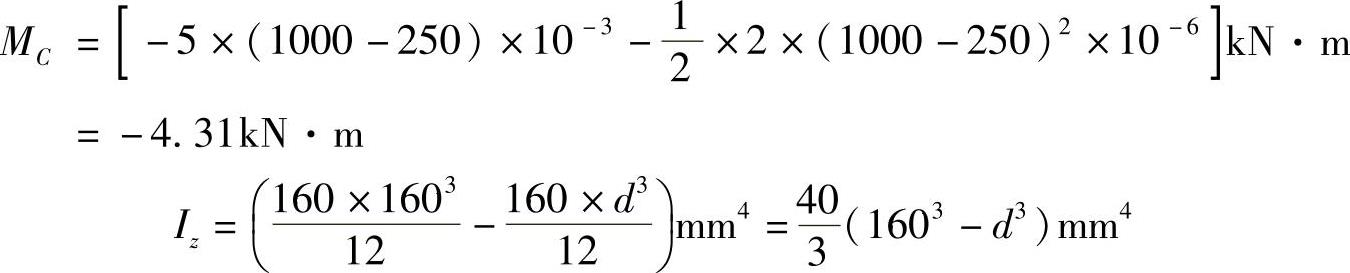
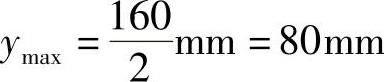
由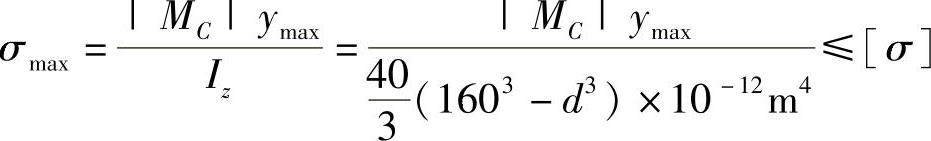，可得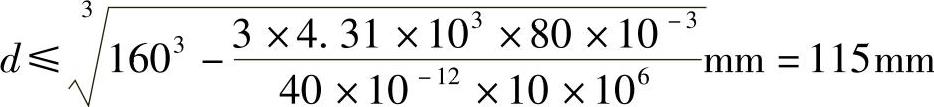

例5-6 图5-9a所示T形截面铸铁梁承受载荷作用。已知铸铁的许用拉应力[σ_t]=40MPa，许用压应力[σ_c]=160MPa。试按正应力强度条件校核梁的强度。若载荷不变，但将T形横截面倒置成⊥形，是否合理？为什么？

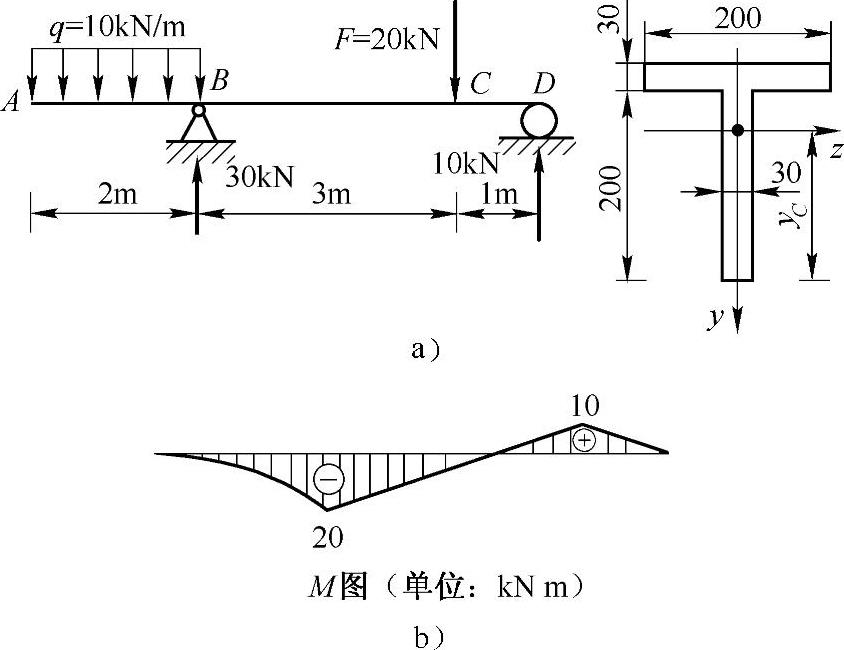
图5-9 例5-6图

解：（1）作M图，如图5-9b所示，求I_zC。

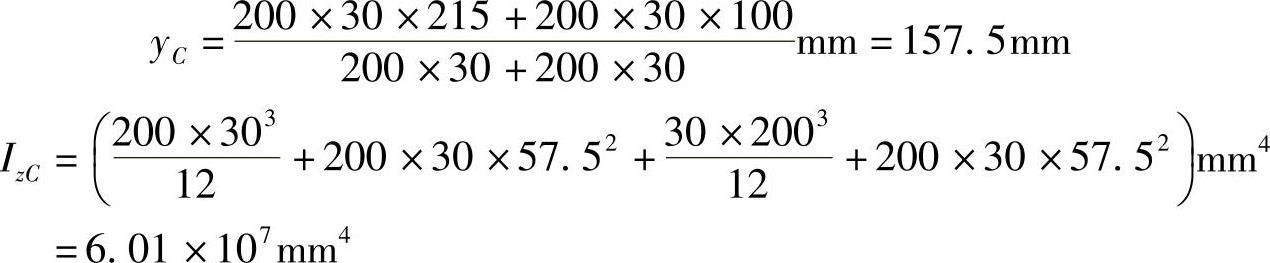
（2）强度校核

B截面：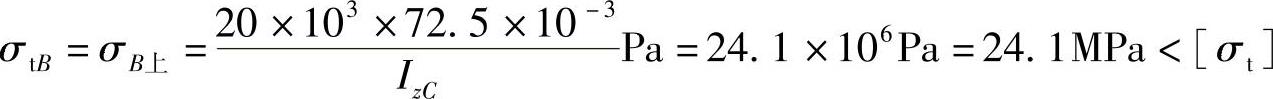

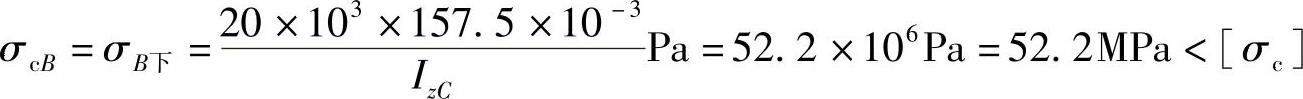
C截面：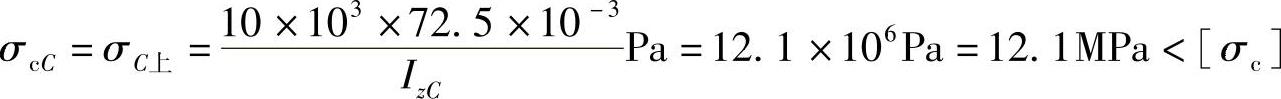

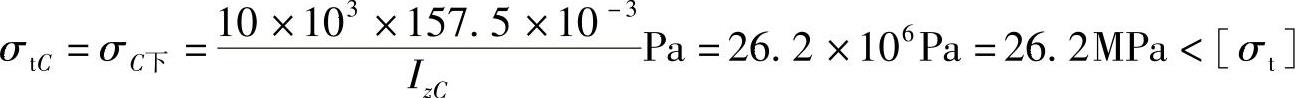
（3）若倒置成⊥形时，σ_tB=σ_B上=52.2MPa＞[σ_t]，所以不合理。

例5-7 若图5-10a所示梁的许用正应力[σ]=160MPa，许用切应力[τ]=100MPa，试选择工字钢的型号。

解：（1）求支反力，作剪力、弯矩图，如图5-10b、c所示

F_Smax=22kN，M_max=16.2kN·m

（2）按正应力强度条件选择工字钢型号。

由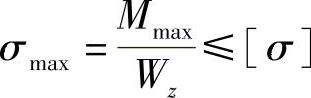，得到

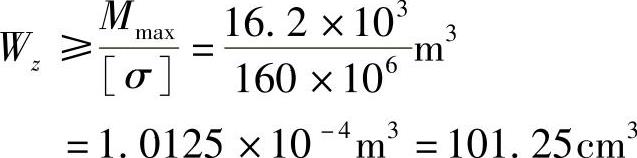
查表选14工字钢，其中，

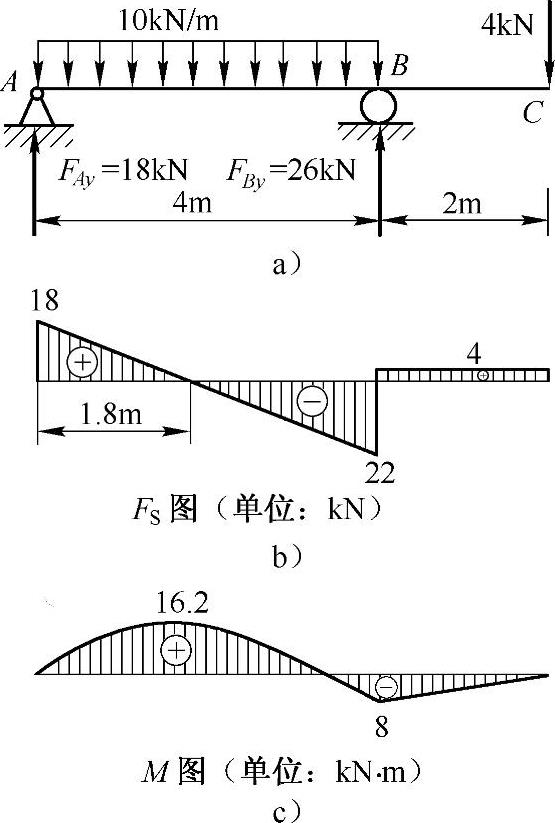
图5-10 例5-7图

W_z=102cm³，b=5.5mm，I_z/S_z∗=12.0cm

（3）切应力强度条件校核。

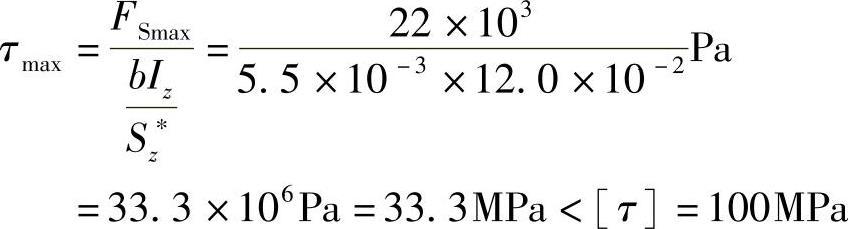
满足切应力强度条件。

综上所述，所以选择14工字钢。