3.3  例题解析

3.3 例题解析

例3-1 试作如图3-1a所示圆轴的扭矩图，并求B截面相对A截面的相对扭转角及AB段中最大相对扭转角（相对于截面A）。设T，a，G，d均为已知，t是均布扭转力偶矩的集度。

解：扭矩图如图3-1b所示，有

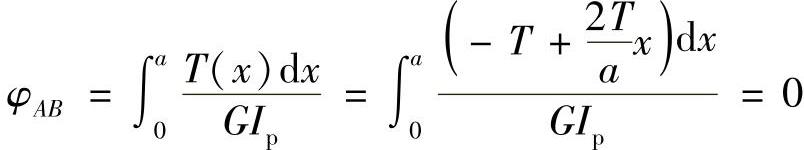
AB段内对A截面最大相对扭转角是a/2处截面对A截面的扭转角，即

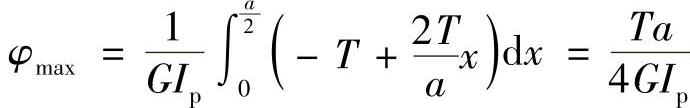
例3-2 图3-2a所示为一端固定，另一端自由的圆轴，承受的载荷是按线性规律分布的分布力偶t（x），其最大分布集度为t₀。已知轴长为L，直径为d，材料的切变模量为G。（1）试绘出扭矩图；（2）求B端扭转角φ_AB。

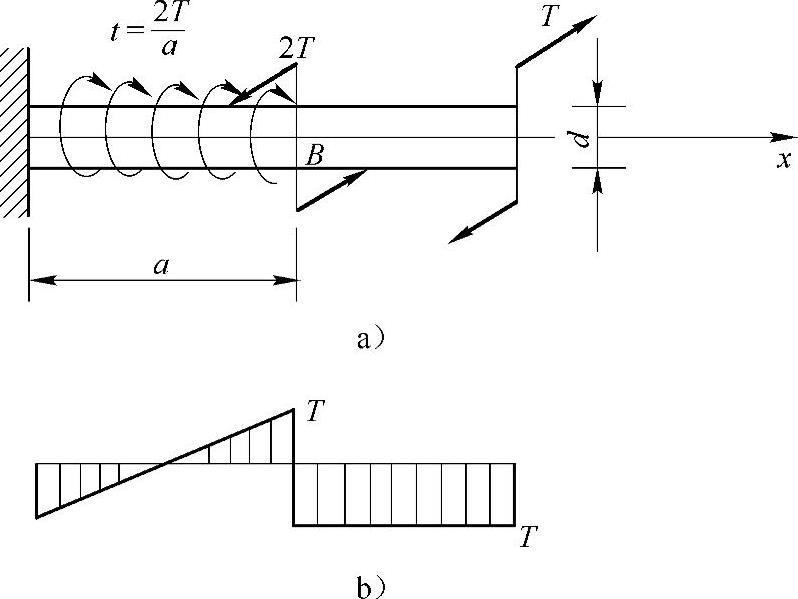
图3-1 例3-1图

解：（1）作扭矩图，有

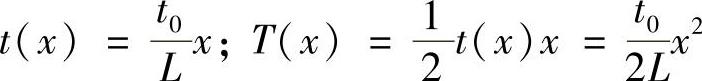
扭矩图如图3-2b所示。

（2）如图3-2a所示，在x处取dx微段，其两端的相对扭转角为

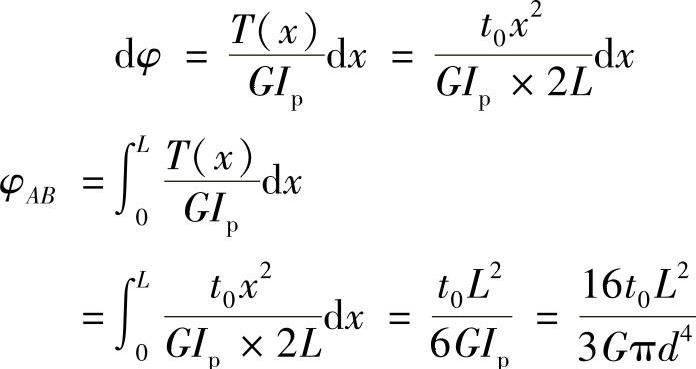
例3-3 有三根轴，横截面面积、杆长和材料均相同，截面形状分别为圆形、正方形和h/b=2的矩形，试比较它们的抗扭刚度。

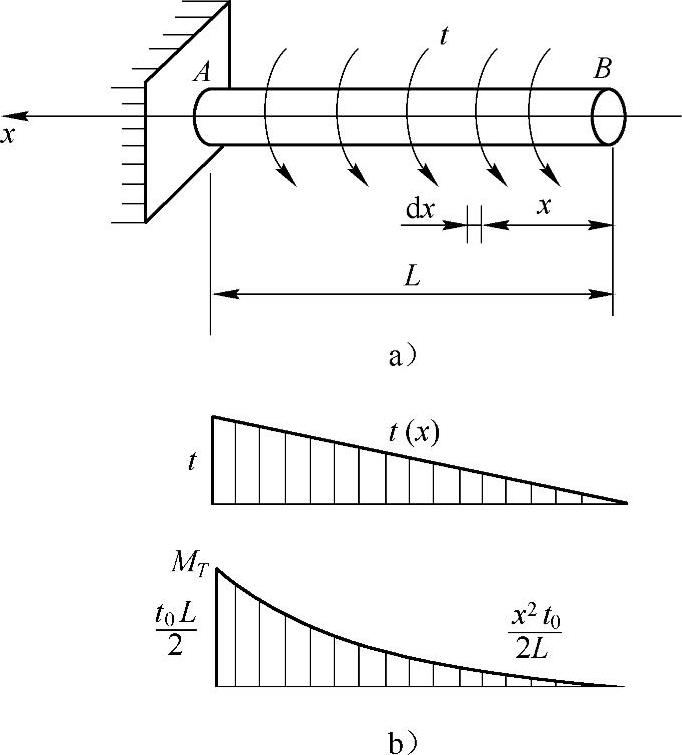
图3-2 例3-2图

解：设圆形截面的直径为d，正方形截面的边长为a；根据题意知矩形截面的高为h，宽为b。

由面积相等得πd²/4=a²=hb，且h/b=2，由此得到，’。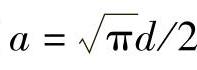

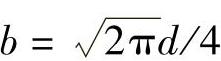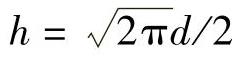对于矩形截面，杆件抗扭刚度计算公式为

GI_t=Gβb³h

其中，对于正方形截面杆件，β=0.141，则GI_t=0.0869d⁴G。

对于h/b=2的矩形截面杆件，β=0.229，则，GI_t=0.0706d⁴G。

对于圆形截面，杆件抗扭刚度为。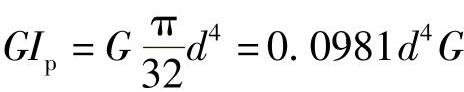

所以圆形截面、正方形截面和矩形截面杆件的抗扭刚度之比为

GI_p∶GI_t1∶GI_t2=1∶0.886∶0.720

例3-4 图3-3所示圆轴，其端部AB段截面因安装手轮被加工成正方形。设正方形边长为a，圆轴直径为d。试从强度方面求轴的许用扭矩因此降低了多少百分率？

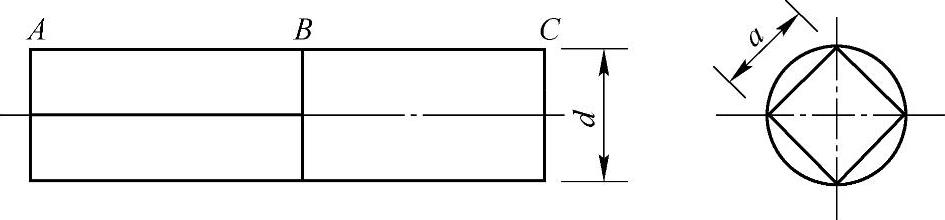
图3-3 例3-4图

解：由图得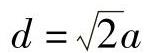

正方形：α=0.208，，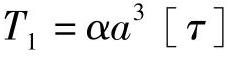

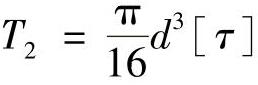
则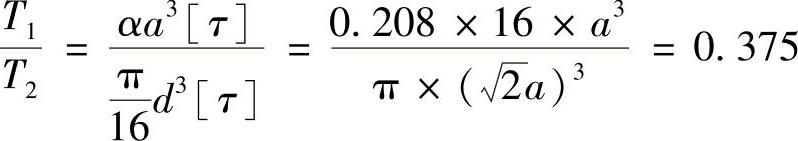

降低百分率为（1-0.375）×100%=62.5%。

例3-5 密圈螺旋弹簧，簧圈平均半径R=20mm，材料许用切应力[τ]=480MPa，切变模量G=80GPa，若欲使该弹簧在轴向载荷F=1kN作用下恰好产生λ=30mm的轴向变形，试确定弹簧丝的直径d和弹簧的圈数n。

解：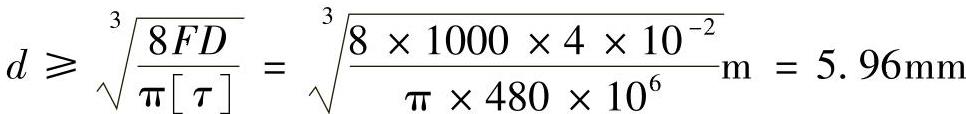

若取d=6mm，则

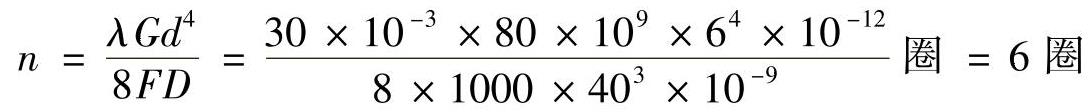
例3-6 圆轴受力如图3-4a所示，外直径为D，孔直径d=D/2，材料的切变模量为G，又设长度a，力偶矩M均为已知。（1）画轴的扭矩图；（2）求A截面的扭转角。

解：（1）轴的扭矩图如图3-4b所示。

（2）由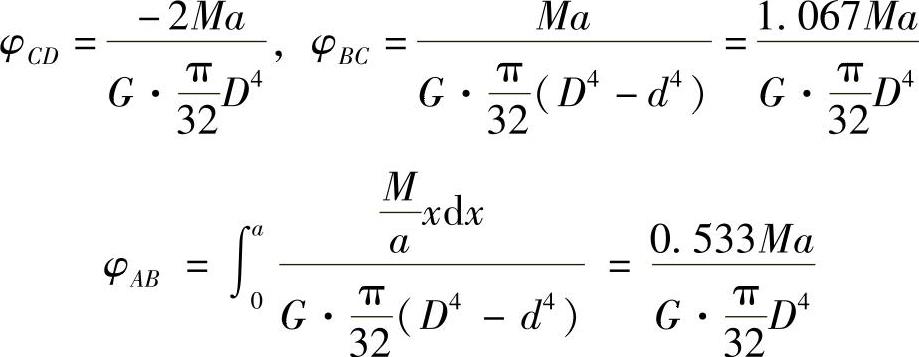

故A端扭转角为

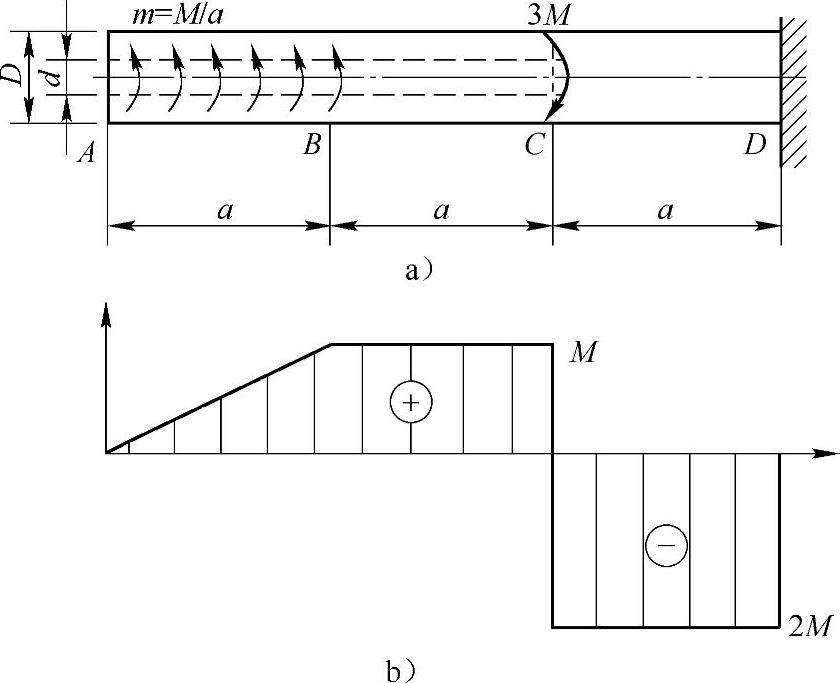
图3-4 例3-6图

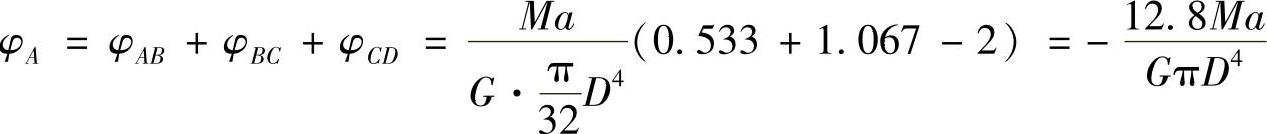
例3-7 如图3-5所示圆截面杆AB左端固定，承受均布力偶作用，其力偶矩集度为m=20（N·m）/m。已知直径d=20mm，l=2m，材料的切变模量G=80GPa，[τ]=30MPa，单位长度的许用扭转角[φ]=2（°）/m。试进行强度和刚度校核，并计算A，B两截面的相对转角φ_BA。

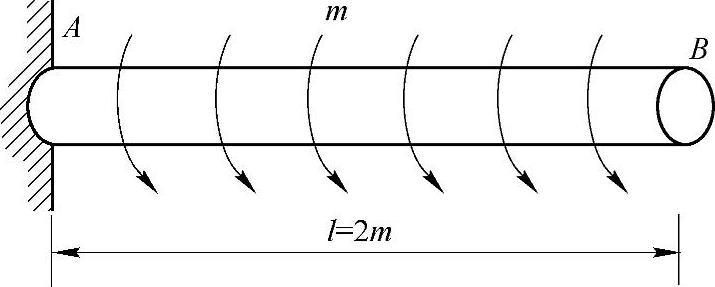
图3-5 例3-7图

解：（1）强度校核。A截面扭矩最大，其值为

T_max=ml=20（N·m）/m×2m=40N·m

最大切应力为

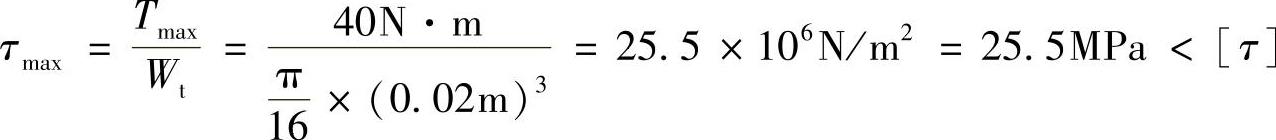
所以满足强度条件。

（2）刚度校核。杆单位长度最大扭转角为

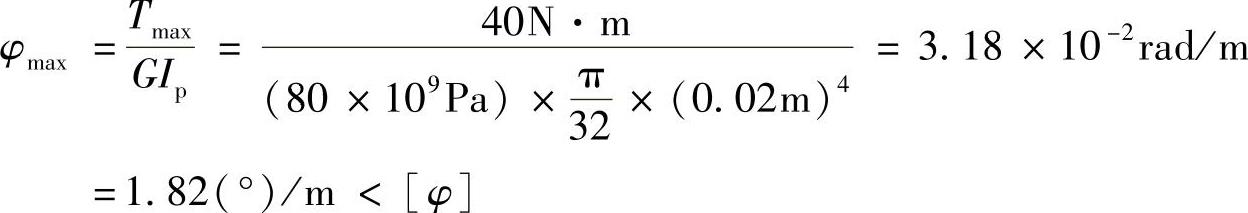
所以满足刚度条件。

（3）A，B两截面的相对扭转角为

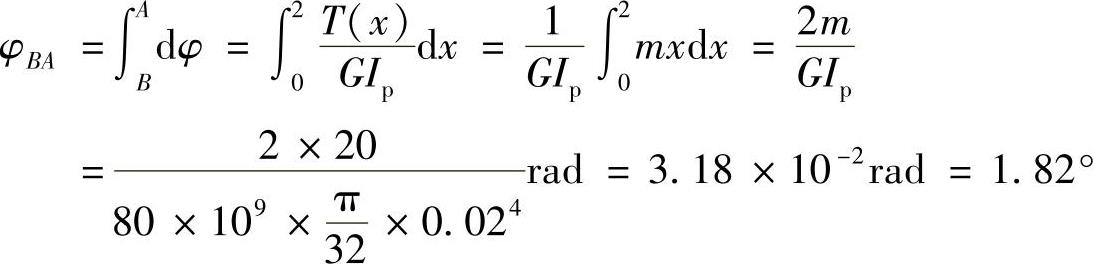
例3-8 如图3-6a所示传动轴的转速n=600r/min，主动轮2输入功率P₂=350kW，从动轮1，3，4分别输出P₁=100kW，P₃=130kW，P₄=120kW。已知[τ]=60MPa，[φ]=1（°）/m，G=80GPa，试画出该传动轴的扭矩图，并确定该等直径传动轴的直径。

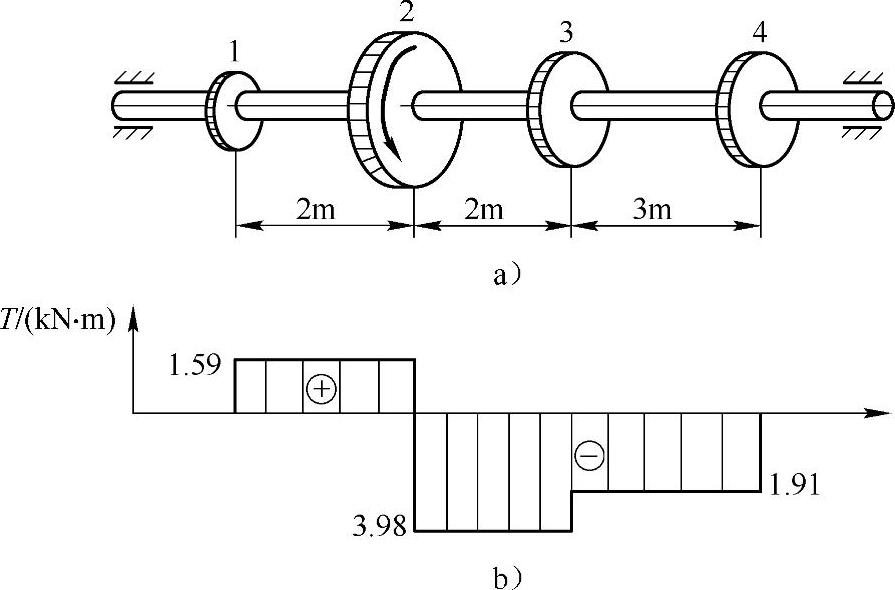
图3-6 例3-8图

解：根据功率转化为扭矩的关系，1，2，3，4各截面的扭矩分别如下：

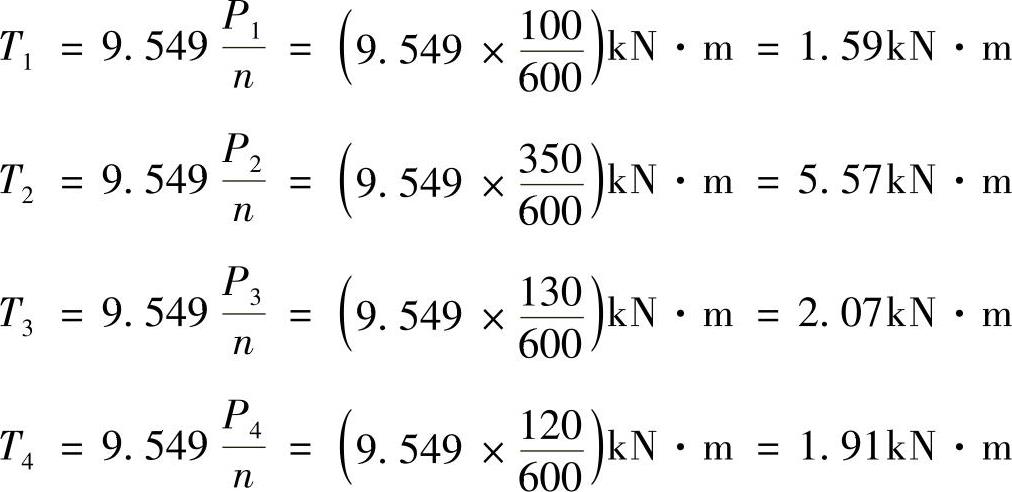
扭矩图如图3-6b所示。

由强度条件有

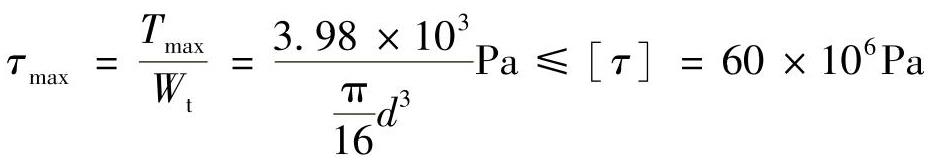
求得 d≥0.07m

由刚度条件有

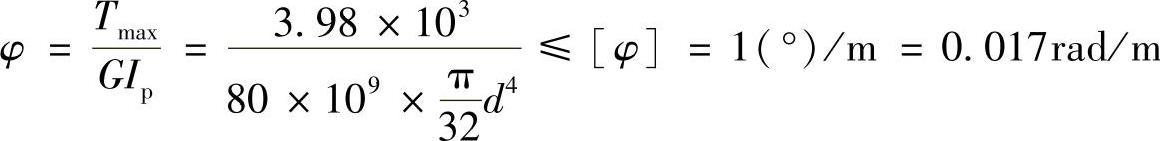
求得d≥0.074m，所以，该轴直径应不小于74mm。

例3-9 如图3-7所示两端固定的阶梯圆轴，在截面C上受扭转力偶矩T_C的作用。已知D₁=7cm，D₂=5cm，[τ]=60MPa，试求最大的扭转力偶矩T_C。

解：设AC段扭矩为T₁，BC段扭矩为T₂，则由平衡条件有

T₁+T₂=T_C （a）

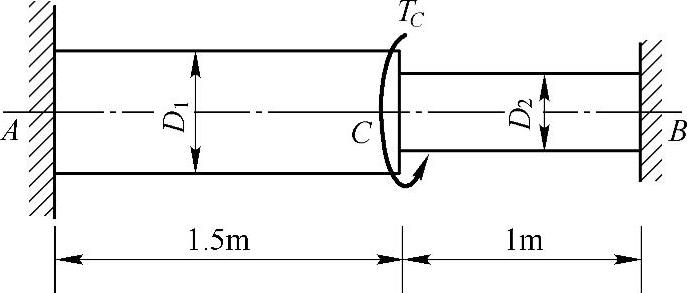
图3-7 例3-9图

变形条件为C截面左右两侧转角相等，即

φ_CA=φ_CB，即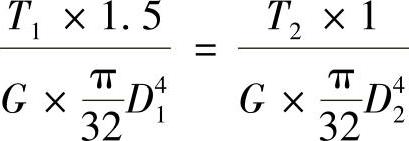

从而有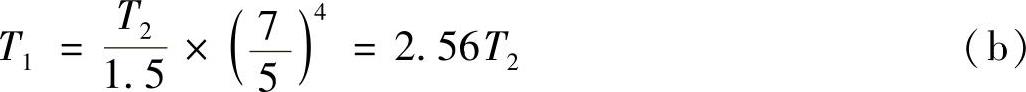

由式（a）、式（b）解得

T₁ =0.72T_C，T₂=0.28T_C

列强度条件如下：

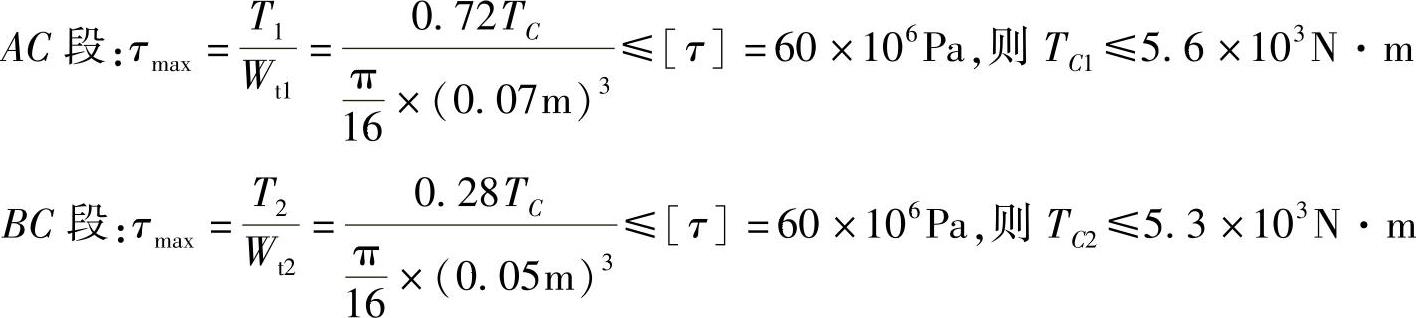
所以[T_C]=5.3×10³N·m。

例3-10 如图3-8所示，一组合轴由直径d=75mm的钢杆与外面紧包的黄铜管组成。已知切变模量G_钢=80GPa，G_铜=10GPa。试问：（1）如果组合轴两端受扭转力偶T作用，两种材料分担同样大小的力偶矩，则黄铜管的外径D为多少？（2）如果T=16kN·m，则每种材料中产生的最大扭转切应力为多少？

解：设钢杆为1杆，铜杆为2杆。

（1）两杆扭转角相等，即φ₁=φ₂，即

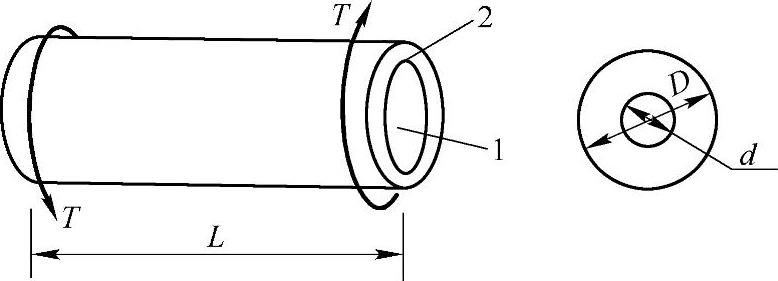
图3-8 例3-10图

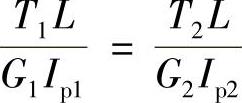
因T₁=T₂，所以G₁I_p1=G₂I_p2，即

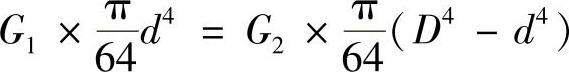
则 G₁d⁴=G₂（D⁴-d⁴）

从而得到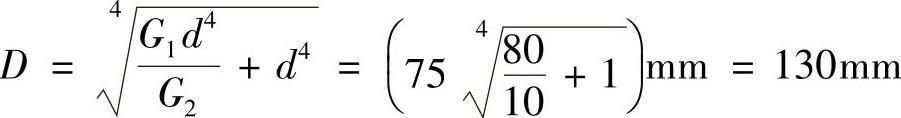

（2）最大切应力

实心钢轴：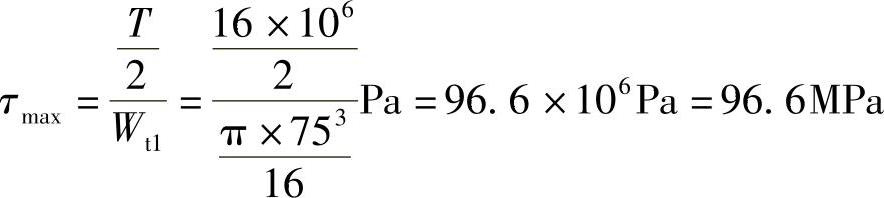

空心铜管：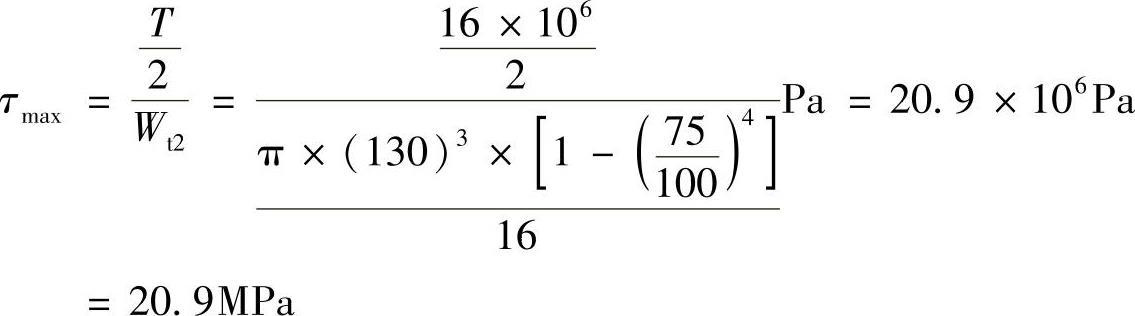

例3-11 有一薄壁圆管的平均直径为R，壁厚为t。另有一实心圆轴的直径为D，二者材料相同，横截面面积相同，长度均为L，各自承受不同扭矩，如果二者的最大切应力相同。试问：管的应变能与实心轴的应变能之比值是多少？

解：设薄壁圆管为杆1，实心轴为杆2。则

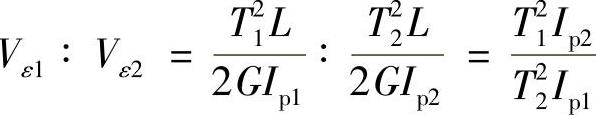
又τ_1max=τ_2max，即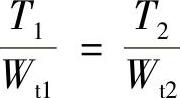

又A₁=A₂，即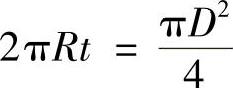

所以

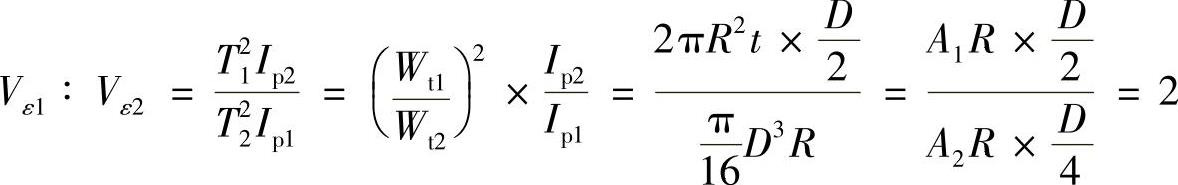
即V_ε1∶V_ε2=2∶1。

例3-12 如图3-9所示，实心轴和空心轴通过牙嵌离合器连接，已知轴的转速n=120r/min，传递功率P=8.5kW，材料的许用切应力[τ]=45MPa。试确定实心轴的直径D₁和内、外径比α=0.5的空心轴的外径D₂。

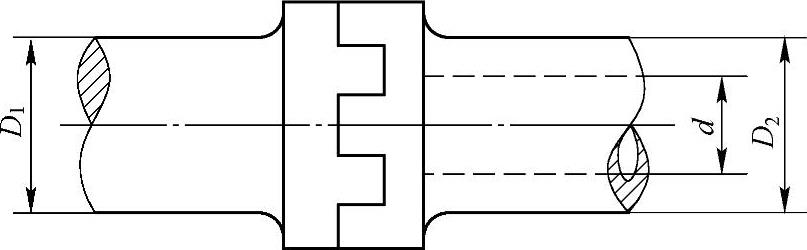
图3-9 例3-12图

解：轴传递的扭矩

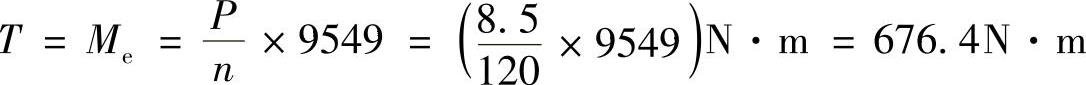
根据扭转圆轴的强度条件

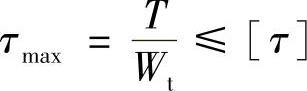
对于实心轴，有

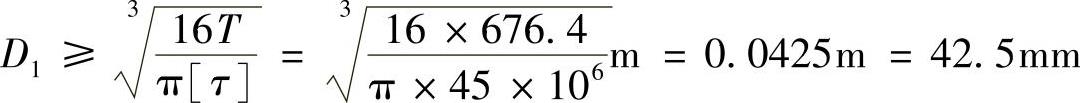
故可取实心轴的直径为D₁=43mm。

对于空心轴，则有

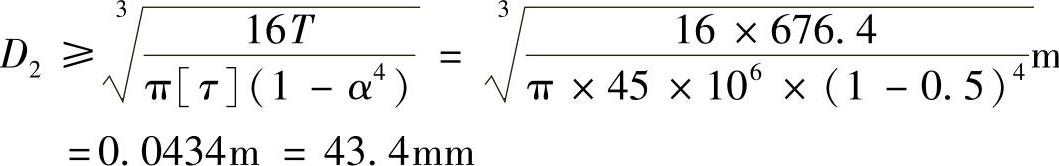
故可取空心轴的直径为D₂=44mm。