4.1.5 载荷集度、剪力和弯矩间的关系
2025年10月13日
4.1.5 载荷集度
、剪力和弯矩间的关系
(1)直梁q(x),FS(x)和M(x)间的导数关系: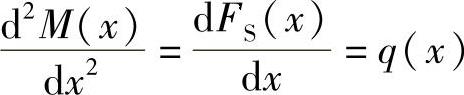 。公式的几何意义是:①剪力图上某点处的切线斜率等于该点处载荷集度的大小;②弯矩图上某点处的切线斜率等于该点处剪力的大小。
。公式的几何意义是:①剪力图上某点处的切线斜率等于该点处载荷集度的大小;②弯矩图上某点处的切线斜率等于该点处剪力的大小。
(2)在几种载荷下剪力图与弯矩图的特征(表4-1)
表 4-1
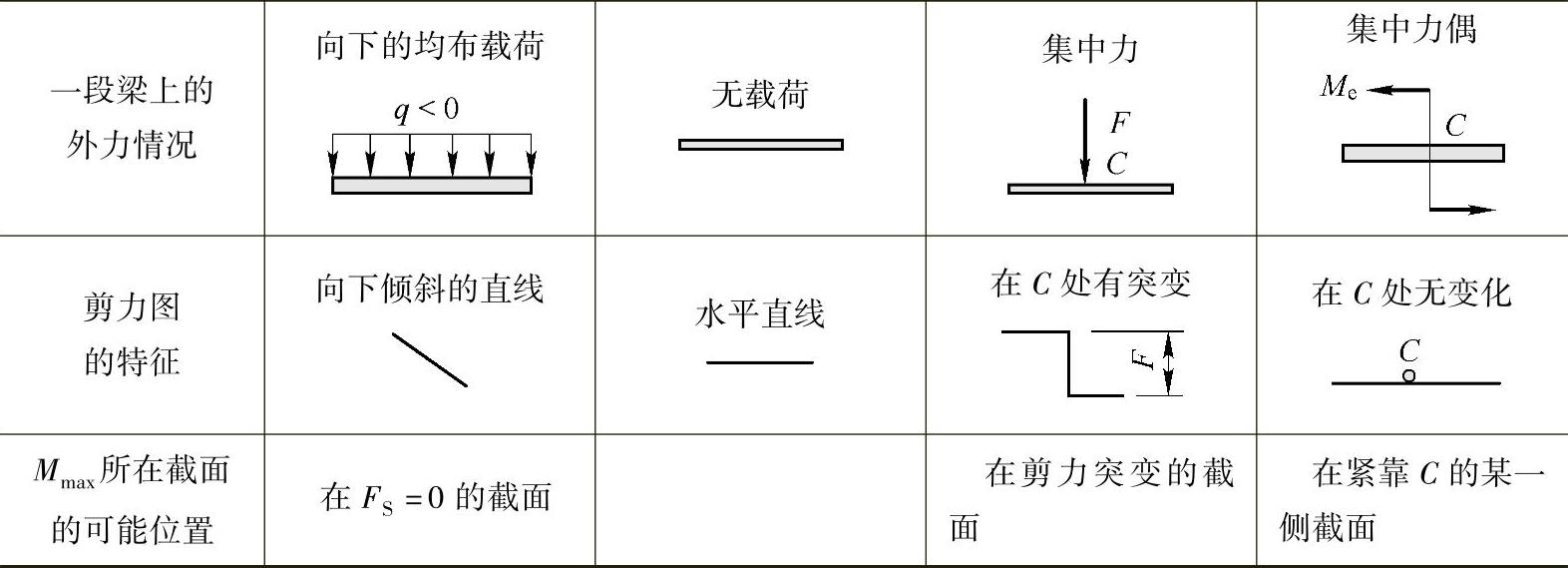
(3)q(x),FS(x)和M(x)间的积分关系
1)当两个横截面间无集中力作用时,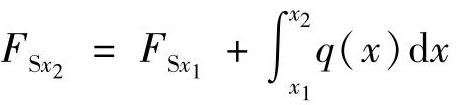 ,式中,
,式中,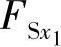 和
和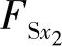 分别为在x=x1和x=x2处两个横截面上的剪力,等号右边积分的几何意义是,上述两横截面间分布载荷图的面积。
分别为在x=x1和x=x2处两个横截面上的剪力,等号右边积分的几何意义是,上述两横截面间分布载荷图的面积。
2)当两个横截面间无集中力偶作用时,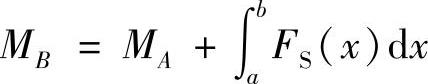 ,式中,MA和MB分别为在x=a和x=b处两个横截面上的弯矩,等号右边积分的几何意义是两个横截面间剪力图的面积。
,式中,MA和MB分别为在x=a和x=b处两个横截面上的弯矩,等号右边积分的几何意义是两个横截面间剪力图的面积。
(4)叠加原理:多个载荷同时作用于结构而引起的内力等于每个载荷单独作用于结构而引起的内力的代数和。适用条件:所求参数(内力、应力、位移)必然与载荷满足线性关系,即在弹性限度内满足胡克定律。
(5)按叠加原理作弯矩图
步骤:①分别作出各项载荷单独作用下梁的弯矩图;②将其相应的纵坐标叠加。
