首页> 图书频道> 工学> 工业技术

6.4  习题

2025年10月13日
版权
6.4 习题

习题6-1 用积分法求如图6-6所示梁A截面的挠度和B截面的转角。EI为已知常数。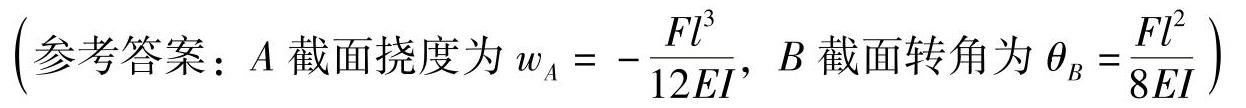978-7-111-43425-2-Chapter06-34.jpg

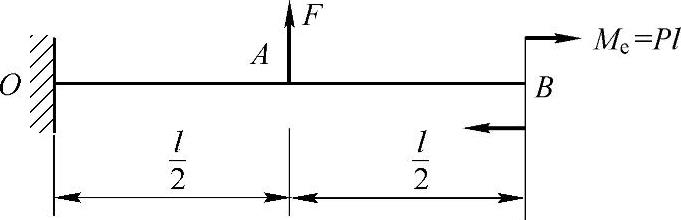
978-7-111-43425-2-Chapter06-35.jpg

图6-6 习题6-1图

习题6-2 简支梁受三角形分布载荷作用，如图6-7所示。

978-7-111-43425-2-Chapter06-36.jpg

图6-7 习题6-2图

（1）试导出该梁的挠曲线方程；

（2）确定该梁的最大挠度。

978-7-111-43425-2-Chapter06-37.jpg

习题6-3 用叠加法求如图6-8所示各梁截面A的挠度和转角。EI为已知常数。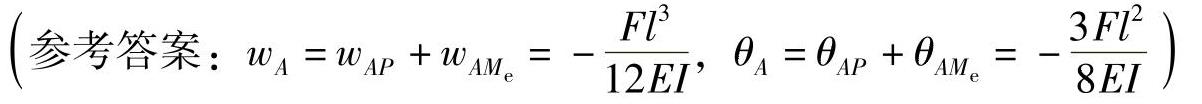978-7-111-43425-2-Chapter06-38.jpg

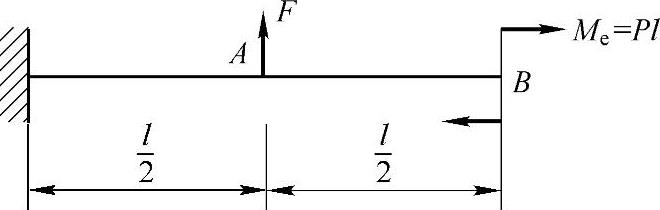
978-7-111-43425-2-Chapter06-39.jpg

图6-8 习题6-3图

习题6-4 图6-9所示悬臂梁的抗弯刚度EI=30kN·m2，弹簧的刚度k=175×103N/m，梁端与弹簧间的空隙为δ=1.25mm。当F=450N时，试问弹簧将分担多大的力？（参考答案：Ft=82.6N）

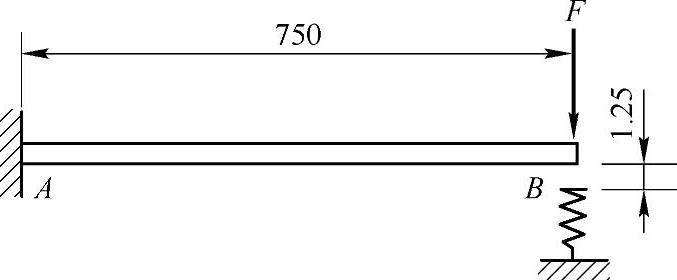
978-7-111-43425-2-Chapter06-40.jpg

图6-9 习题6-4图

习题6-5 用叠加法求图6-10所示

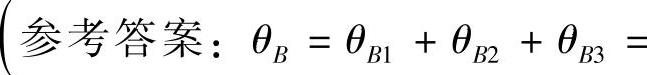
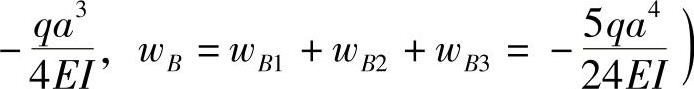
外伸梁外伸端的挠度和转角，设EI为常量。978-7-111-43425-2-Chapter06-41.jpg978-7-111-43425-2-Chapter06-42.jpg

习题6-6 图6-11所示悬臂梁AD和BE的抗弯刚度同为EI=24×106N·m2，由钢杆CD相连接。CD杆的长度l=5m，横截面积A=3×10-4m2，弹性横量E=200GPa。若F=50N，试求悬臂梁AD在D点的挠度。（参考答案：wD=-0.56mm）

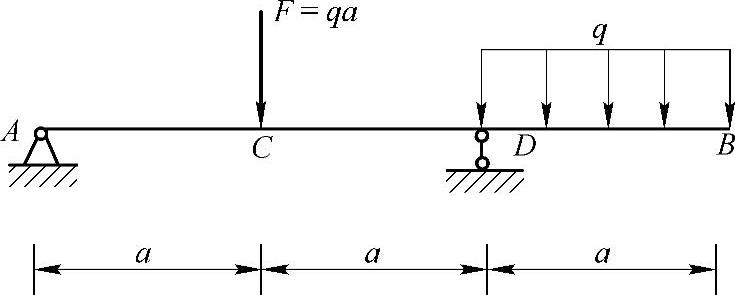
978-7-111-43425-2-Chapter06-43.jpg

图6-10 习题6-5图

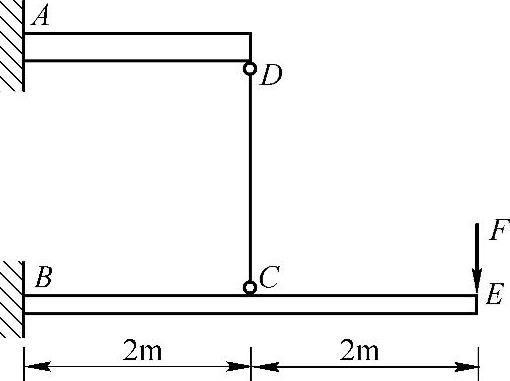
978-7-111-43425-2-Chapter06-44.jpg

图6-11 习题6-6图