基于层次分析法的博士后评估
1970年T.I.SAATY 教授提出一种多则决策方法Analytic Hierarchy Process,简称AHP(层次分析)法[1],该方法作为一种定性与定量分析相结合的综合性评价方法,具有简便、灵活、实用等特点,在多个领域得到广泛应用。鉴于层次分析法能将复杂问题进行有效分解,拟用层次分析法对博士后研究人员评估指标体系进行评价。建立合理的博士后评估指标体系是进行评估工作的前提和基础[2]。在借鉴结构方程模型思想[3]的基础上,根据一般研究人员能力的判定要素,并考虑博士后的实际情况,对各影响因素进行总结和分析,建立了一个多指标评价体系。该体系共有三个层次,每一个层次的评价指标都是由上一个层次的评价指标拓展而来,上一个层次的指标评价结果又是下一个层次指标评价结果的反馈。第一级为目标层,是博士后综合能力的总体评价,其权重为A;第二级为准则层,为反映博士后能力不同侧面的4项评价指标,包括科研绩效(第一或者主要完成人)、创新性、复合性、成果产出,其权重为(B1、B2、B3、B4),对指标进行两两比较,得到一个判断矩阵;第三级是第二级指标的进一步细化,由体现不同方面的44项指标构成。
层次分析法作为一种科学的决策分析方法,在评价博士后综合能力方面,彰显出较大的优越性,在很大程度上摒弃了人的主观性,有助于保证结果的客观和有效性。由于各评价指标在整个体系中的地位及重要性均有差异,因此需要根据其重要性进行赋值,可采用专家打分法将各个因素进行评定[4]。在采用层次分析法进行问题分析时,构造问题的判断矩阵是其中最重要的环节。构造判断矩阵的方法是:将每个具有向下隶属关系的因子作为判断矩阵的第一个影响因子,其包含的每个影响因子排列在其后的第一行以及第一列中。根据层次分析法相关准则,对每两个影响因子做两两一组的判断,其重要性标度值具体如表5.2所示[5]。
表5.2 重要性标度含义表

假设判断矩阵为A=(aij)n×n,依据数学方法对其进行单层次的排序[6]。一致性检验的步骤[7]如下。
(一)计算一致性指标C.I.(Consistency Index)的计算
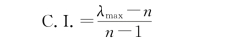
(二)平均随机一致性指标R.I.(Random Index)的确定(https://www.daowen.com)
对n=1,…,9,Saaty用数学随机方法利用500个样本值构造出相应矩阵,并分析了R.I.的值,如表5.3所示。
表5.3 R.I.的值

表5.3是Saaty从n=1,…,9的数字及其倒数中随机地选取任意数字建立的正互反矩阵,可得到λmax的平均值![]() ,并有
,并有
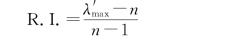
(三)对一致性比例C.R.进行分析比较
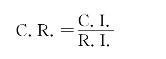
若C.R.<0.1,构造出的A 一致性可以被接受;若C.R.>0.1,构造出的A 不可接受,因此需对A 进行修订。
