10.1.4 受力特点及影响因素
组合梁斜拉桥桥面板剪力滞后、混凝土收缩徐变、钢-混界面滑移等多种效应互相关联,精细化分析才能对其准确模拟。概念设计中应抓住主要矛盾,适当简化。
1.剪力滞后效应
目前各国规范对梁式桥桥面板有效宽度作了规定,但该规定并不适用于组合梁斜拉桥。组合梁斜拉桥主梁不仅承受弯矩而且承受轴力,因此分别对应有弯矩有效分布宽度及轴力有效分布宽度。弯矩有效分布宽度与有效跨度有关,而轴力有效分布宽度与拉索水平轴力的扩散相关。理论上讲,桥轴向同一位置有效分布宽度在不同施工阶段及成桥阶段不断变化,而且由于在正常使用状态及承载能力状态下主梁轴力、弯矩所占比例不同,桥面板有效宽度也理应有所区别。
同时考虑主梁两种有效分布宽度,在设计计算中会带来不便。相比之下,在弯矩和轴力共同作用下的桥面板有效宽度系数更易于实际操作。对组合梁斜拉桥桥面板统一有效宽度系数的研究表明,重庆江津观音岩长江大桥的有效宽度系数在0.75~0.95,武汉二七长江大桥的有效宽度系数在0.748~0.916。基于美国已建18座组合梁斜拉桥基本参数,在理论分析基础上,拟合出适合于组合梁斜拉桥的修正有效分布宽度折线图(见图10.3),发现有效宽度仅与主梁竖向支座的纵向间距、桥面板板厚及桥面实际宽度有关。值得注意的是,主塔处主梁有无竖向支座,对该区域桥面板有效宽度影响较大。与国内相关研究相比,除支座附近有效宽度更为不利以外,国内外研究结论总体上较为吻合。
2.收缩徐变效应
组合梁斜拉桥混凝土收缩徐变有其自身规律,其整体时变响应总体上是不利的,在结构设计时必须考虑。以两塔斜拉桥为例,成桥后混凝土收缩徐变将引起索力的变化,特别是边跨拉索索力会较大幅度地减小。索力改变将使主塔上塔柱水平力不再平衡,塔顶向中跨偏移,塔底出现向中跨侧顺桥向弯矩,主梁中跨下挠,全长出现不同程度的负弯矩及轴向拉力。相应地,主梁桥面板产生不同程度的拉应力,钢主梁压应力则有较大幅度的增加。独塔斜拉桥则由于结构体系的不同,收缩徐变的影响相对较小。
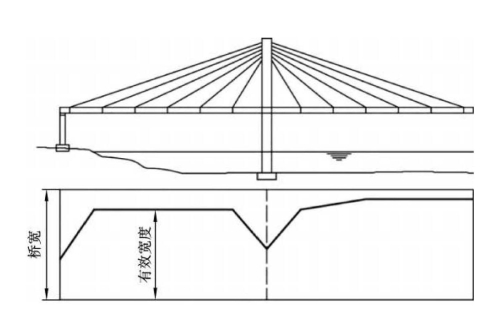
图10.3 组合梁斜拉桥桥面板有效分布宽度(https://www.daowen.com)
组合梁斜拉桥主梁在承受负弯矩或轴向拉力时会表现出其不利的一面,为了减轻组合梁的收缩徐变效应,可延长混凝土桥面板龄期。另外,不同结构体系下组合梁斜拉桥的时效响应有所不同。在主塔处设置竖向支座时,主塔收缩徐变将使梁塔交接处主梁产生局部负弯矩峰值。设置辅助墩除使辅助墩附近主梁出现负弯矩峰值外,将使组合梁斜拉桥的整体时变效应更为明显。在体系确定时,单纯从时变效应角度来讲,全漂浮体系(主塔处无支座、不设置辅助墩)较其他体系更为合理。
3.连接件设计及其滑移效应
混凝土桥面板与钢梁之间一般采用剪力钉连接,结合成整体后共同受力。对大跨组合梁斜拉桥,一方面应考虑剪力钉自身受力,另一方面须考虑其柔性对结构整体受力是否产生影响。
组合梁斜拉桥界面连接件设计时,应考虑竖向荷载、拉索索力、预应力、收缩徐变等荷载的作用及其组合,尤其应注意辅助墩处、拉索锚固点、预应力束端部等位置的剪力钉合理布置。在实际工程设计时,对于剪力钉滑移,主要考虑其对剪力钉自身受力的影响,而基本不须考虑对主梁钢结构及混凝土桥面板等其他结构静力响应的影响。
4.非线性及稳定
对大跨斜拉桥,基于非线性有限元施工过程模拟得到的成桥状态,是进行结构运营荷载、动力、稳定等方面精确分析的基础。非线性可分为几何非线性及材料非线性。关于拉索垂度、P-δ、大位移等几何非线性效应,组合梁斜拉桥与其他斜拉桥并无本质上的区别。混凝土材料的徐变、塔梁间纵向非线性约束、钢-混界面滑移等均属于材料非线性范畴。精确计算时,应对各项非线性效应进行同步计算,简单的叠加原理不再适用。千米级组合梁斜拉桥几何非线性效应研究表明,几何非线性使结构活载效应均有不同程度增加,影响系数在15%以内,收缩徐变工况受几何非线性的影响相对较小,影响系数在5%以内。
随着斜拉桥跨径的不断增大,桥塔高耸化、主梁纤细化使稳定问题更为突出。在不同的施工阶段及成桥阶段,不同斜拉桥在不同的荷载条件下,塔、梁均可能成为稳定控制因素。由于主梁自重原因,对千米级组合梁斜拉桥应重点关注主梁面内失稳问题。
