第一节  函数

第一节 函数

一、区间与邻域

1.区间

定义1.1 满足不等式a＜x＜b（a＜b）的所有实数x的集合，称为以a、b为端点的开区间，记作（a，b）.

类似地，有闭区间[a，b]={x|a≤x≤b}，半开区间（a，b]={x|a＜x≤b}和[a，b）={x|a≤x＜b}，它们称为有限区间.而区间（a，+∞）、[a，+∞）、（-∞，a）、（-∞，a]称为无限区间.

2.邻域

定义1.2 设a∈R，δ>0，数集{x|x-a＜δ}称为a的δ邻域，记为

U（a，δ）={x||x-a＜δ}=（a-δ，a+δ）.

a称为邻域的中心；δ称为邻域的半径.常又表示为U（a），简称为a的邻域.

去掉中心a的数集{x|0＜x-a＜δ}称为a的去心δ邻域，记为

U°（a，δ）={x|0＜x-a＜δ}=（a-δ，a+δ）-{a}.

常又表示为U°（a），简称为a的去心δ邻域.

类似地，数集{x|0＜x-a＜δ}称为a的右邻域，数集{x|-δ＜x-a＜0}称为a的左邻域.

二、函数概念

1.变量

在研究数学的过程中常常涉及到各种各样的量，其中，变化的量称为变量，不变化的量称为常量或常数.函数是考察变量之间关系的重要概念.

例如，球的半径r与该球的体积V的关系为

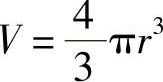
式中，π是圆周率，它是常量.

对于任意r∈[0，+∞），都对应一个球的体积V.r和V都是变量，它们之间的关系可以用函数来表达.

2.函数定义

定义1.3 设D是非空数集，若对D中任意数x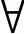（x∈D），按照某一确定的对应法则f，总有唯一确定的数y∈R与之对应，则称f是定义在D上的函数，记为

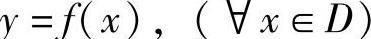
简写为“y=f（x）”，或称“f（x）是x的函数（值）”.其中，数x称为自变量，数y称为因变量.

数集D称为函数f的定义域，函数值的集合f（D）={f（x）|x∈D}称为函数f的值域.函数的两要素为定义域和对应法则，与变量用何符号表示没有关系.

3.单值函数与多值函数

在函数y=f（x）的定义中，要求对应于x值的y值是唯一确定的，这种函数也称为单值函数.如果取消唯一这个要求，即对应于x值，可以有两个以上确定的y值与之对应，那么函数y=f（x）称为多值函数.例如，函数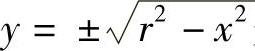是多（双）值函数.

以后若不特别声明，只讨论单值函数.

4.函数举例

例1 取整函数y=[x]，表示对于任意x∈R，对应的y是不超过x的最大整数.

如[2.5]=2，[3]=3，[0]=0，[-π]=-4，图形（见图1-1）.

例2 符号函数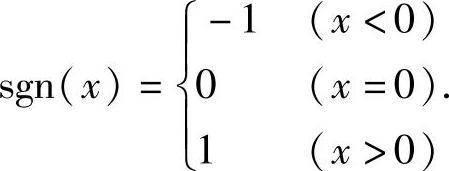

例3 绝对值函数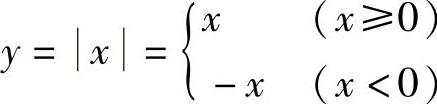，图形（见图1-2）.

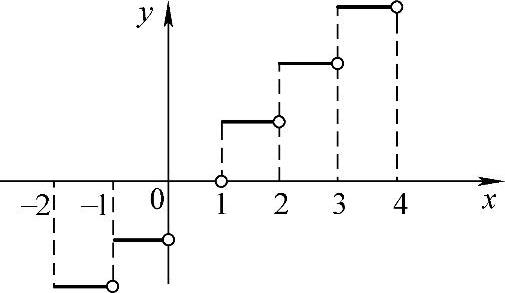
图1-1

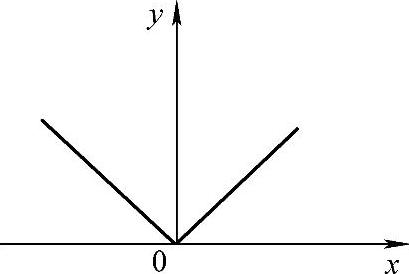
图1-2

上述几个函数的定义域被分成了若干部分，而在不同部分上，函数值用不同的表达式表示，这样的函数称为分段函数.

三、函数性质

1.有界性

定义1.4 设函数f（x）在数集A上有定义，若存在M>0，使得任意x∈A，有f（x）≤M，则称函数f（x）在A上有界，否则称f（x）在A上无界.

例如，函数y=sinx在（-∞，+∞）内是有界的，因为对于任意x∈R，都有|sinx≤1.函数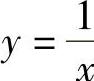在（0，1）内是无界的，在[2，+∞）上是有界的.

2.单调性

定义1.5 设函数f（x）在数集A上有定义，若对任意x₁，x₂∈A，当x₁＜x₂时，有f（x₁）＜f（x₂）（或f（x₁）＞f（x₂）），则称函数f（x）在A上是严格单调增加（或严格单调减少）的；若将上述不等式改为f（x₁）≤f（x₂）（或f（x₁）≥f（x₂）），则称函数f（x）在A上是单调增加（或单调减少）的.

例如，函数y=x³在（-∞，+∞）内是严格单调增加的.函数y=2x²+1在（-∞，0）内是严格单调减少的，在[0，+∞）内是严格单调增加的.因此，y=2x²+1在（-∞，+∞）内不是单调函数.

3.奇偶性

定义1.6 设函数f（x）定义在数集A上，若对于任意x∈A，有-x∈A，且

f（-x）=-f（x）（或f（-x）=f（x））

则称函数f（x）是奇函数（或偶函数）.奇函数的图像关于原点对称，偶函数的图像关于y轴对称.

例如，函数y=x⁴+3x²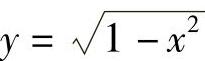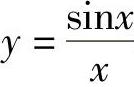，，都是偶函数.函数y=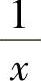，y=x³，y=xcosx都是奇函数.

4.周期性

定义1.7 设函数f（x）定义在数集A上，若存在l>0，对于任意x∈A，有x±l∈A，且f（x±l）=f（x），则称函数f（x）是周期函数，l称为函数f（x）的周期.

由定义可知，周期不唯一.若l是函数f（x）的周期，则2l也是它的周期，nl（n∈N）也是它的周期.若函数f（x）有最小的正周期，通常称之为函数f（x）的基本周期，简称为周期.

例如，正弦函数y=sinx就是周期函数，周期为2π.再如，常数函数y=1也是周期函数，任意正实数都是它的周期，它没有基本周期.

四、复合函数与反函数

1.复合函数

定义1.8 设函数z=f（y）定义在数集B上，函数y=φ（x）定义在数集A上，且φ（A）⊂B（φ（A）是B的一个非空子集）.对于任意x∈A，按照对应关系φ，对应唯一一个y∈B，若再按照对应关系f，对应唯一一个z，即对于任意x∈A，对应唯一一个z.于是可以在A上定义一个函数，表示为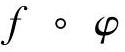，称为函数y=φ（x）与z=f（y）的复合函数，即

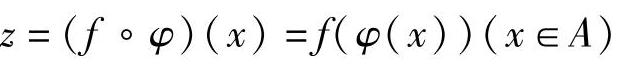
其中，y称为中间变量.

例如，函数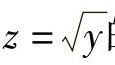的定义域是区间[0，+∞），函数y=1-x²的定义域是R.为使其生成复合函数，必须要求

y=1-x²≥0，即-1≤x≤1于是，对于任意x∈[-1，1]，函数y=1-x²与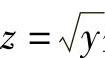生成了复合函数

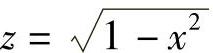
又如，3个函数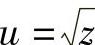，z=lny，y=2x+3，生成的复合函数是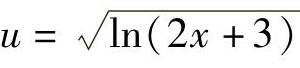,x∈[-1，+∞）.

2.反函数

定义1.9 设函数y=f（x），x∈I.若对任意y∈f（I），有唯一确定的x∈I与之对应，使f（x）=y，则在f（I）上定义了一个函数，记为

x=f^-1（y），y∈f（I）

称为函数y=f（x）的反函数.原来的函数y=f（x）称为直接函数.

按照书写习惯，将自变量写成x，因变量写成y，所以反函数x=f^-1（y）常常被写作y=f^-1（x）.

反函数y=f^-1（x）的图像与直接函数y=f（x）的图像关于直线y=x对称（见图1-3）.

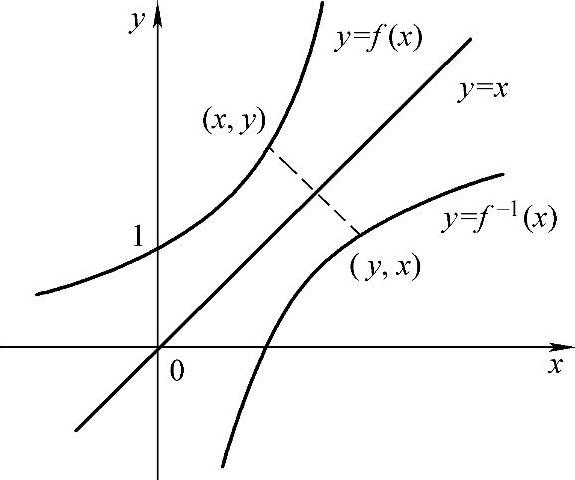
图1-3

定理1.1 若函数y=f（x）在某区间I上严格单调增加（或严格单调减少），则函数y=f（x）存在反函数，且反函数x=f^-1（y）在f（I）上也严格单调增加（或严格单调减少）.

定理1.1中“严格”两字不可忽略.如单调函数y=[x]（取整函数）非严格单调，不存在反函数.

函数是严格单调的仅是存在反函数的充分条件，如函数

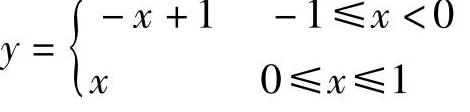
在区间[-1，1]上不是单调函数，但它存在反函数

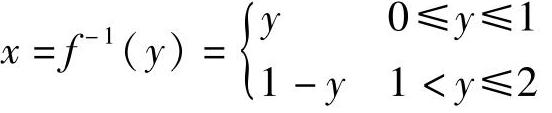
五、初等函数

1.基本初等函数

（1）常数函数

y=C；

（2）幂函数

y=x^α；

（3）指数函数

y=a^x，（a>0，a≠1）.特例y=e^x；

（4）对数函数

y=log_ax，（a>0，a≠1）.特例y=lnx；

（5）三角函数

y=sinx，y=cosx，y=tanx，y=cotx，y=secx，y=cscx；

（6）反三角函数

y=arcsinx，y=arccosx，y=arctanx，y=arccotx.

2.初等函数的定义

定义1.10 由常数和基本初等函数经过有限次的四则运算和有限次的函数复合步骤所生成的并可用一个式子表达的函数称为初等函数.

例如，函数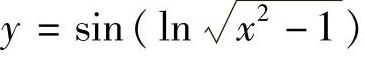是一个初等函数，它是由y=sinu，u=lnv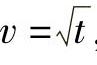，，t=x²-1经过四则运算及复合而得.

由定义可知，那些不能用一个式子表达的分段函数，都不是初等函数.