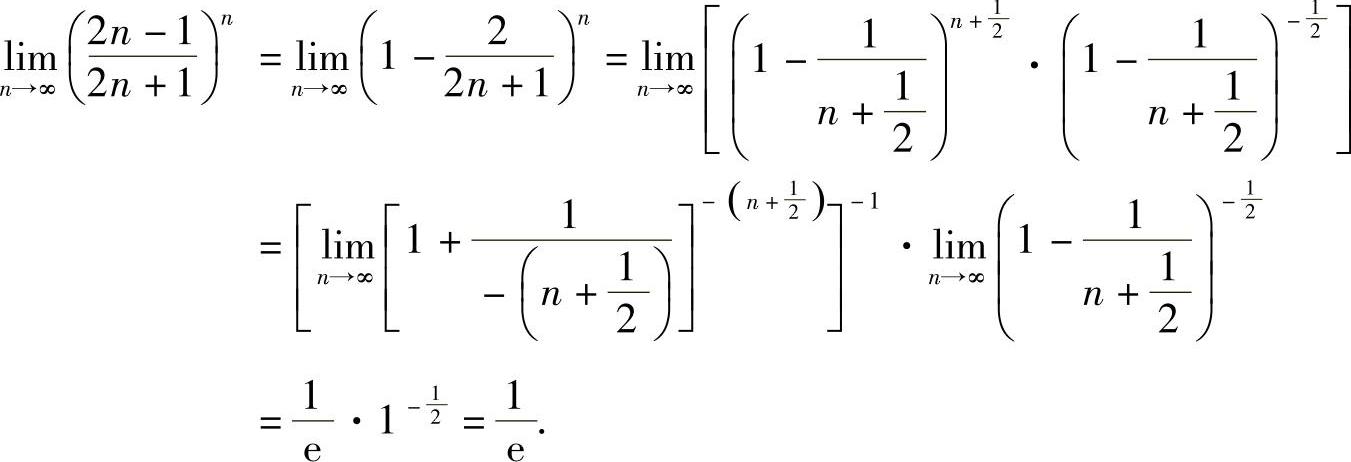两个重要极限

第五节 两个重要极限

一、极限存在准则Ⅰ与第一个重要极限

1.准则Ⅰ（夹逼准则）

定理1.11 若函数f（x）、g（x）、h（x）在点x₀的某去心邻域内满足条件：

（1）g（x）≤f（x）≤h（x），（2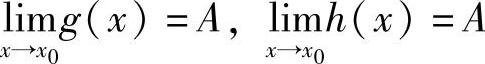），则.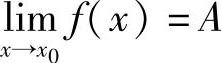

证 对于任意给定的ε＞0，存在δ₁＞0，当0＜|x-x₀|＜δ₁时，有|g（x）-A|＜ε，从而（A-ε）＜g（x），存在δ₂＞0，当0＜|x-x₀|＜δ₂时，有|h（x）-A|＜ε，从而h（x）＜（A+ε），取δ=min{δ₁，δ₂}，则当0＜|x-x₀|＜δ时，有

A-ε＜g（x）≤f（x）≤h（x）＜A+ε

所以有.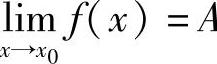

2.第一个重要极限

作为准则Ⅰ的应用，下面将证明第一个重要极限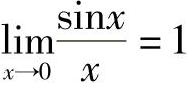

证 由第三节例6，可知sinx＜x＜tanx，以sinx除各项得

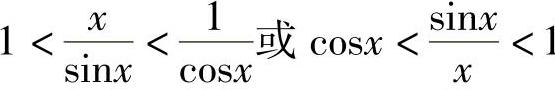
从而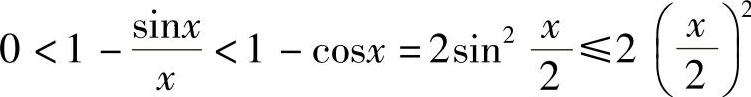.当x→0时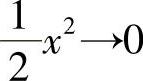，，利用准则Ⅰ，有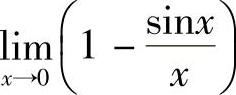=0即.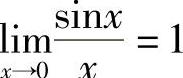

类似地，有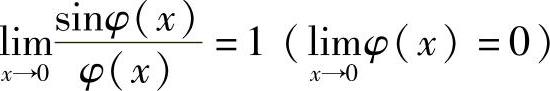（即极限为0的函数的正弦与其本身的比值的极限为1）.

例1 求.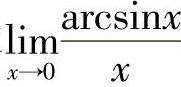

解 令t=arcsinx，则.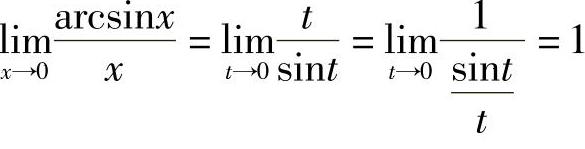

例2 求.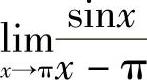

解 令t=π-x，则.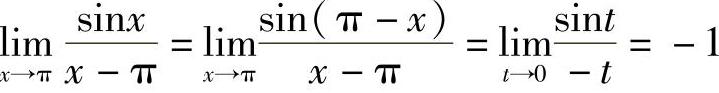

例3 求.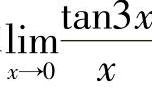

解 .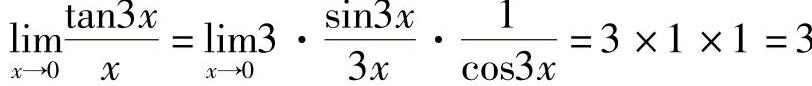

例4 .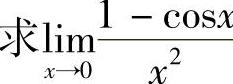

解 .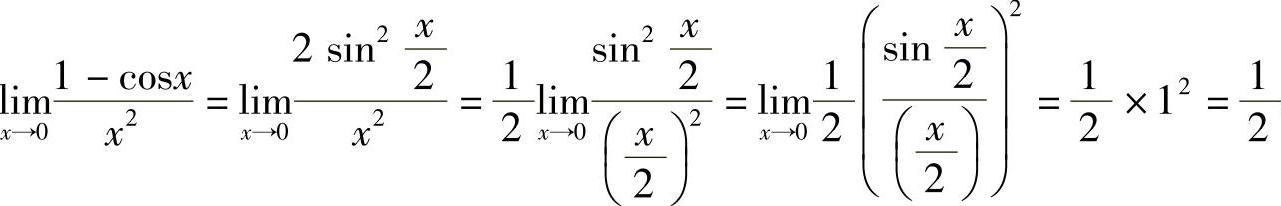

二、极限存在准则Ⅱ与第二个重要极限

1.准则Ⅱ（单调有界准则）单调有界数列必有极限.

如果数列{x_n}满足：x₁≤x₂≤…≤x_n≤x_n+1≤…，就称之为单调增加数列；如果数列{x_n}满足：x₁≥x₂≥…≥x_n≥x_n+1≥…，就称之为单调减少数列；同理亦有严格单增数列或严格单减数列.通称为单调数列和严格单调数列.

如果存在M，使得x_n≤M（n=1，2，…），就称数列{x_n}有上界；如果存在M，使得x_n≥M（n=1，2，…），就称数列{x_n}有下界.统称为有界数列.

准则Ⅱ的证明从略.

准则Ⅱ可推广到函数情形中去，在此不再赘述.

例5 证明数列

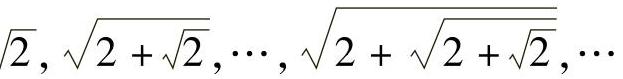
收敛，并求其极限.(https://www.daowen.com)

解 数列显然是单调递增的，是否有界很容易用数学归纳法证明，而且a_n+1=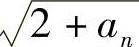，利用单调有界准则，设其极限为A，则有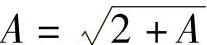，可得A=2.

2.第二个重要极限

作为准则Ⅱ的一个应用，下面来证明第二个重要极限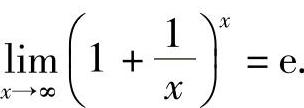

证 设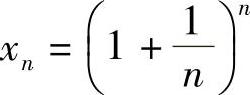，先证明数列{x_n}收敛.对任意的0≤a＜b和正整数n，都满足不等式

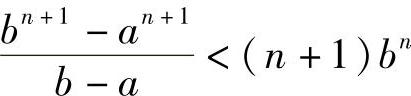
事实上，

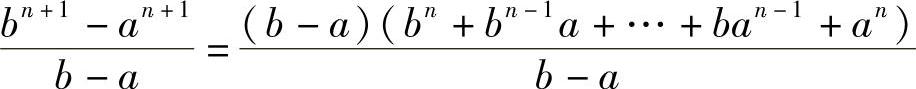
=bⁿ+b^n-1a+…+ba^n-1+aⁿ＜（n+1）bⁿ

该不等式又可变形为

bⁿ[（n+1）a-nb]＜aⁿ⁺¹，（0≤a＜b，n为正整数）

在此不等式中，取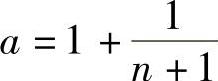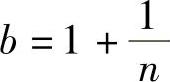，，则有0≤a＜b，就有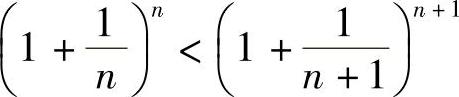，故{x_n}单调增加，

取a=1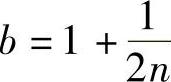，，又有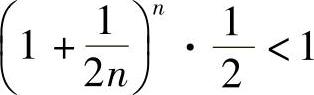对任何正整数n都成立，所以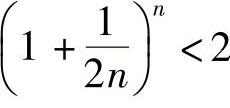，即.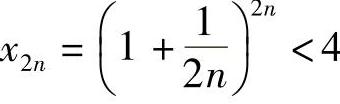

又因为x_2n-1＜x_2n，所以x_n＜4，即数列{x_n}有界.

由单调有界原理，数列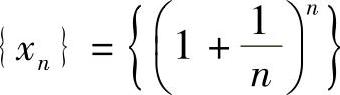有极限，将此极限记为e，则

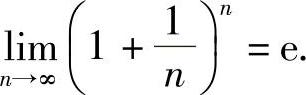
e是一个无理数，它的值是e=2.718281828459045…

类似地，可以证明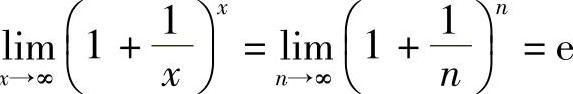，这里从略.

设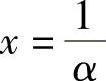，则x→∞⇔α→0，也可以得到.

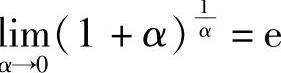类似地，有.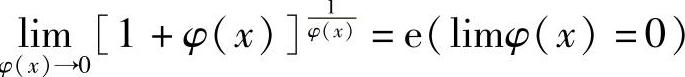

指数函数y=e^x及自然对数y=lnx中的底就是这个常数e.

例6 求.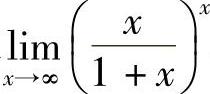

解 .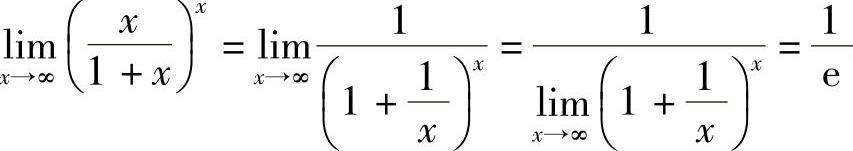

例7 求.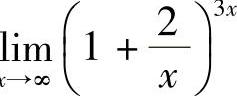

解 令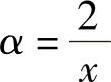，则当x→∞时α→0.故

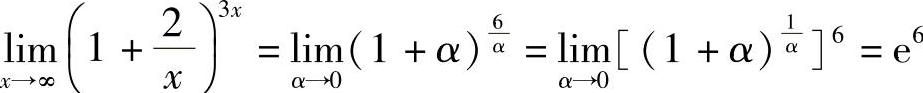
或.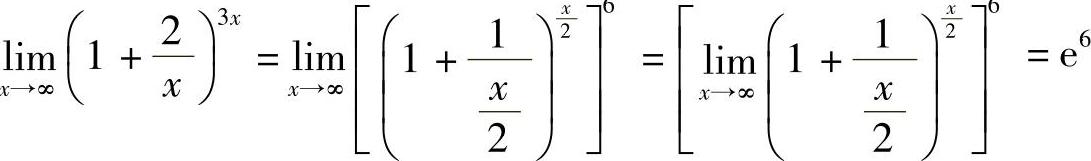

例8 求.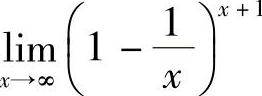

解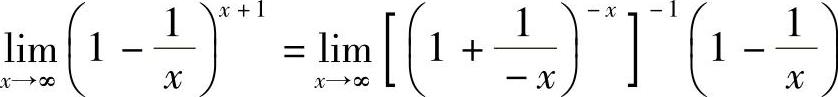

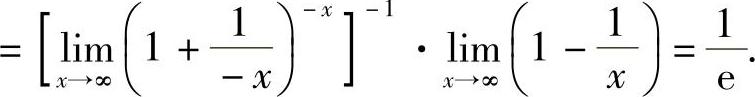
例9 求.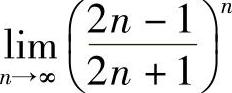

解