高阶导数

第三节 高阶导数

一、高阶导数

一般地，若函数y=f（x）的导数y′=f′（x）仍然可导，这个导数就称为原来函数y=f（x）的二阶导数，记作y″，f″（x）或.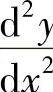

类似地，若y″=f″（x）的导数存在，称为y=f（x）的三阶导数，记作y‴，f‴（x）或.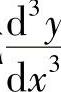

一般地，如果y=f（x）的（n-1）阶导数y（n-1）=f（n-1）（x）的导数存在，其导数就称为y=f（x）的n阶导数，记作y（n），f（n）（x）或.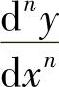

二阶和二阶以上的导数统称为高阶导数.

例1 求n次多项式y=a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n的各阶导数.

解 y′=na₀x^n-1+（n-1）a₁x^n-2+…+a_n-1

y″=n（n-1）a₀x^n-2+（n-1）（n-2）a₁x^n-3+…+2a_n-2

继续求导下去，易知

y（n）=n！a₀它是一个常数，则

y（n+1）=y（n+2）=…=0.

例2 求y=e^x的各阶导数.

解 由（e^x）′=e^x，易知，对任何n，有（e^x）（n）=e^x.

例3 求y=sinx的各阶导数.

解 ，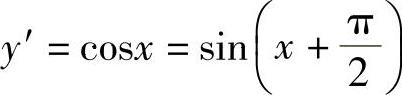

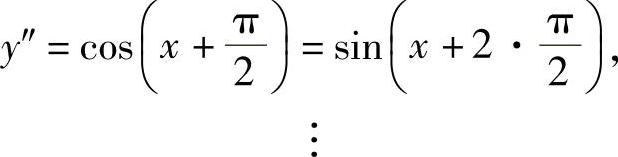
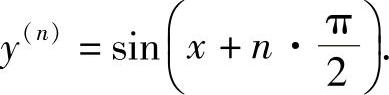
同理可得，.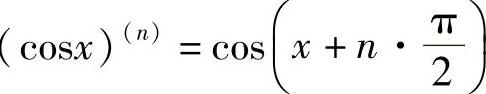

类似于一阶导数的运算法则，高阶导数有如下公式：

1）（u±v）（n）=u（n）±v（n）；2）（Cu）（n）=Cu（n）（C为常数）.

二、隐函数及参数方程所确定的函数的高阶导数

例4 由参数方程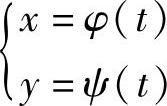确定y为x的函数，若x=φ（t）与y=ψ（t）都是二阶可导的，且φ′（t）≠0，求y对x的二阶导数.

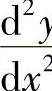解 .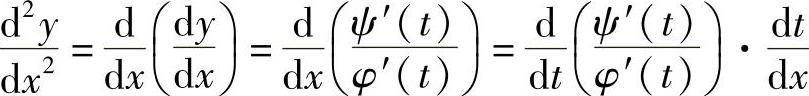

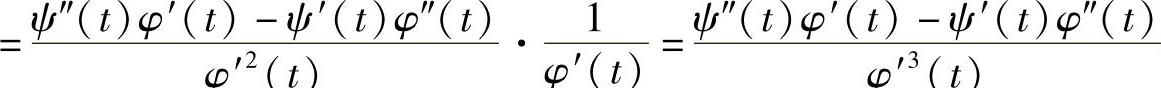例5 求由方程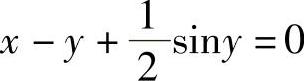所确定的隐函数y的二阶导数.

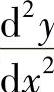解 应用隐函数的求导方法，得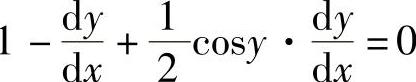，于是.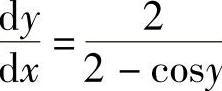

上式两边再对x求导得