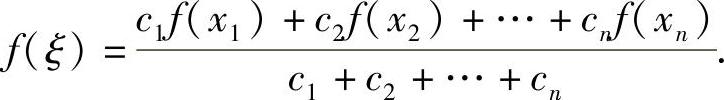函数的连续性
现实生活中，很多变量的变化是连续不断的，比如气温的变化、植物的生长、物体受热时面积的变化等，都是连续的变化.这种现象在数学上用函数的连续性来反映和研究.
一、连续函数的概念
定义1.21 在函数y=f（x）的定义域中，设自变量x由x0变到x1，差Δx=x1-x0叫做自变量x的增量（改变量），相应的函数值的差Δy=f（x1）-f（x0）=f（x0+Δx）-f（x0）叫做函数y=f（x）的增量（见图1-13）.
其中，Δx、Δy是完整的记号，它们可正、可负也可为0.
气温是时间的函数，当时间变化不大时，气温的变化也不大.同样道理，时间变化不大时，植物的生长、物体受热时面积的变化也不大.从这个角度，就可以刻画函数的连续性.
定义1.22 设函数f（x）在x0的某一邻域内有定义，如果当自变量x在点x0处的增量Δx趋于0时，相应的函数增量Δy也趋于0，即
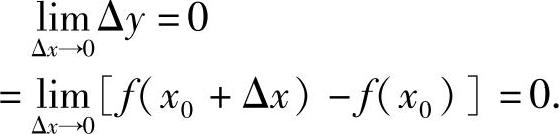
则称函数y=f（x）在点x0连续（见图1-14、图1-15）.
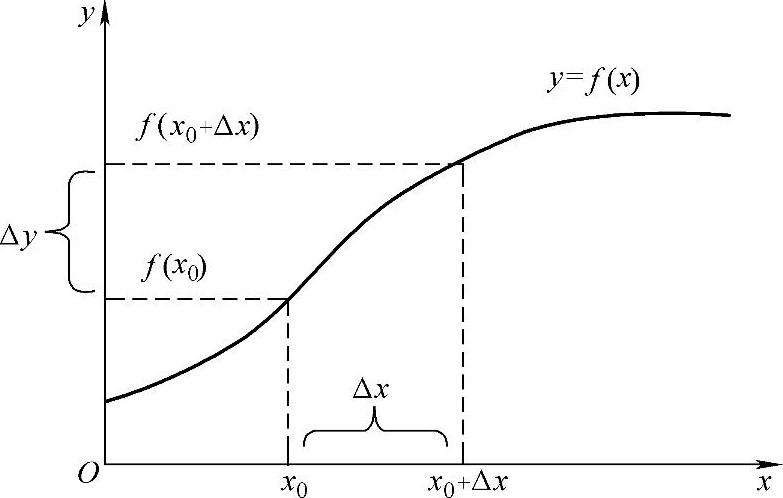
图1-13
在定义1.22中，若令x=x0+Δx，即Δx=x-x0，从而Δx→0等价于x→x0.又Δy=f（x0+Δx）-f（x0）=f（x）-f（x0），从而由连续定义有
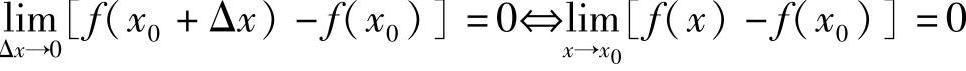
即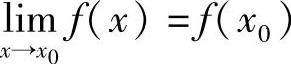
.
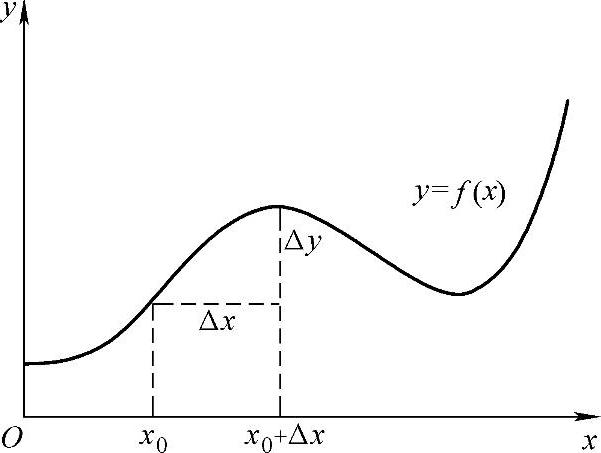
图1-14
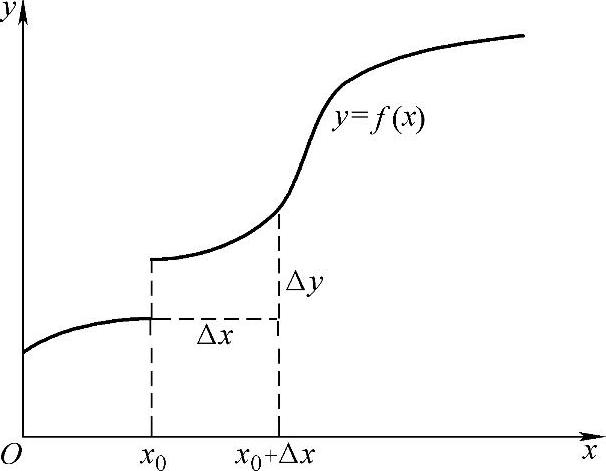
图1-15
定义1.23 设函数y=f（x）在x0的某一邻域内有定义，如果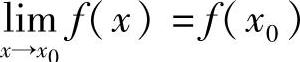
，则称函数y=f（x）在点x0连续.
例1 证明函数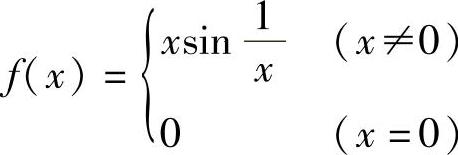
在x=0处连续.
证 因为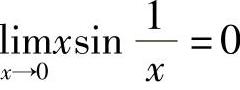
，且f（0）=0，所以
.
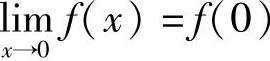由定义可知，函数f（x）在x=0处连续.
根据左、右极限的定义，类似地可以得到左、右连续的定义.
定义1.24 设函数y=f（x）在点x0及其左邻域（或右邻域）内有定义，若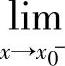
f（x）=f（x0）（或
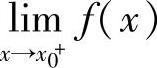=f（x0）），则称函数f（x）在点x0左连续（或右连续）.
显然，函数y=f（x）在点x0处连续的充要条件是函数y=f（x）在点x0处既左连续又右连续.
例2 讨论函数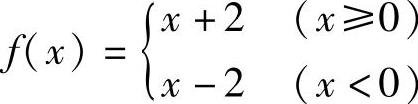
在x=0处的连续性.
解 因为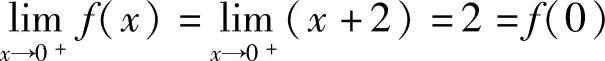
，
.
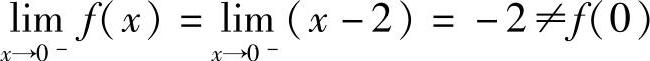所以，函数f（x）在x=0处右连续但不左连续，从而函数f（x）在x=0处不连续.
定义1.25 如果函数f（x）在开区间（a，b）内每一点都连续，则称函数f（x）在区间（a，b）内连续；如果函数f（x）在（a，b）内连续，同时在a点右连续，在b点左连续，则称函数f（x）在闭区间[a，b]上连续.
例如，由极限的运算法则可知，多项式函数f（x）=a0xn+a1xn-1+…+an和有理分式函数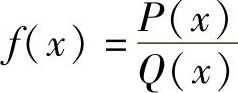
（其中，P（x），Q（x）均为多项式，且Q（x0）≠0）在实数集R内连续.
例3 证明f（x）=sinx在R内连续.
证 任取x0∈R，自变量在x0处获得增量为Δx，令x=x0+Δx.由不等式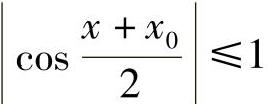
与
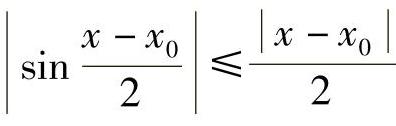
得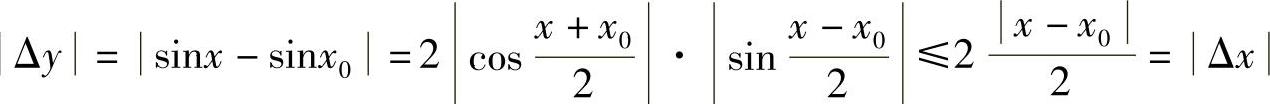
故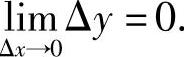
所以正弦函数sinx在x0连续.由x0的任意性，sinx在R内连续.
二、函数的间断点
从连续的定义可知，f（x）在点x0连续必须满足三个条件：
1）f（x）在点x0有确切的函数值f（x0）；
2）当x→x0时，f（x）有确定的极限；
3）这个极限值就等于f（x0）.
定义1.26 如果函数y=f（x）在点x0处不满足连续性条件，则称函数f（x）在点x0间断（或不连续）.点x0称为函数f（x）的间断点（或不连续点）.
显然，f（x）在点x0不满足连续性定义的条件有三种情况：
1）函数f（x）在点x0无定义；2）函数f（x）在点x0有定义，但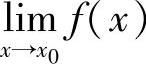
不存在；
3）函数f（x）在点x0有定义，且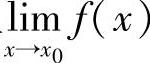
存在，但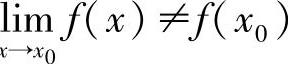
.
对间断点，可按其产生间断的不同原因进行分类.
定义1.27 若f（x）在点x0的左、右极限都存在，但不都等于f（x0），则称点x0是函数f（x）的第一类间断点；
若f（x）在x0的左、右极限至少有一个不存在，则称点x0为f（x）的第二类间断点.
若f（x）在x0的左、右极限存在且相等，但不等于f（x0），或f（x0）无意义，称点x0为f（x）的可去间断点.
例4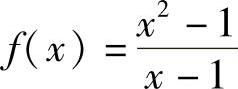 
，讨论f（x）在x=1点处的间断情况.
解 因为
，但f（x）在x=1点无意义，故在x=1处f（x）间断.
若补充定义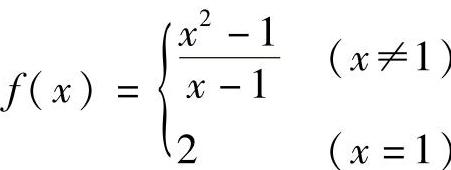
，则f（x）在x=1处连续，x=1是f（x）的可去间断点（见图1-16）.
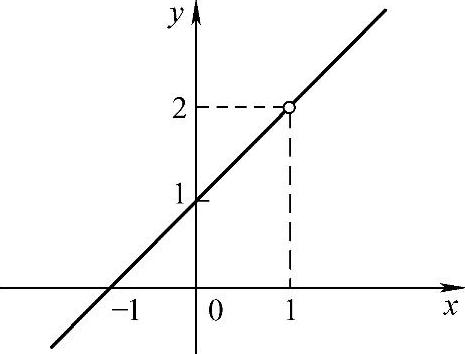
图1-16
例5 设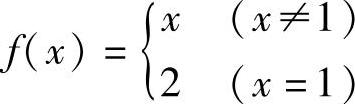
，讨论f（x）在点x=1处的间断情况.
解 因为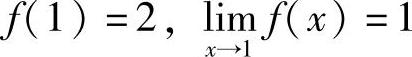
，所以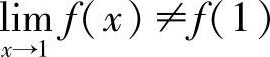
故x=1是f（x）的可去间断点（见图1-17）.
若改变f（x）在x=1处的定义使得f（1）=1，则f（x）在x=1处连续.
若f（x）在x0的左、右极限存在但不相等，则称点x0为f（x）的跳跃间断点.
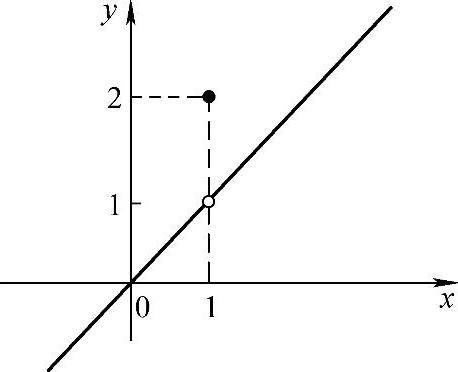
图1-17
例6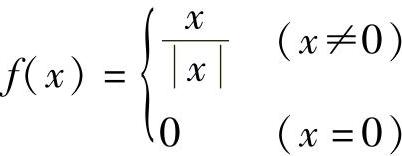 
，讨论f（x）在点x=1处的间断情况.(https://www.daowen.com)
解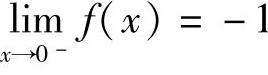 
，
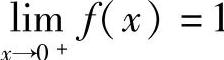，所以x=0是跳跃间断点（见图1-18）.
可去间断点和跳跃间断点都属于第一类间断点.
若f（x）在x0的左、右极限至少有一个是无穷大（∞），则称点x0为f（x）的无穷间断点.
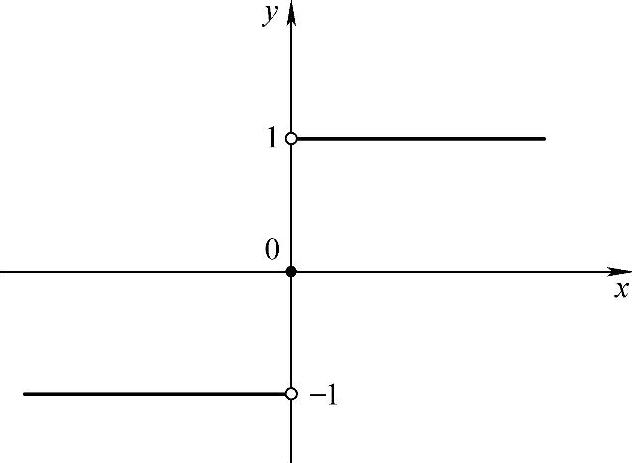
图1-18
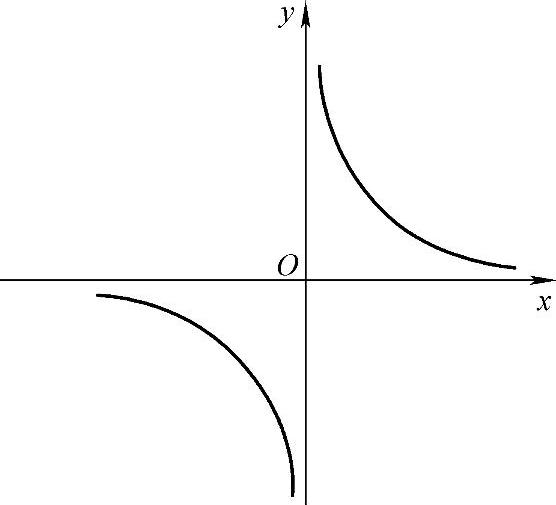
图1-19
例7 设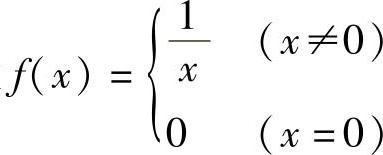
，讨论f（x）在点x=0处的间断情况.
解 函数在点x=0左、右极限都不存在，且都是∞，故x=0是该函数的无穷间断点（见图1-19）.
若f（x）在x0的左、右极限至少有一个是振荡的，则称点x0为f（x）的振荡间断点.
例8 设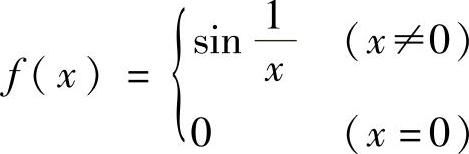
，讨论f（x）在点x=0处的间断情况.
解 函数在点x=0的左、右极限都不存在，且都是振荡的，所以x=0是该函数的振荡间断点（见图1-20）.
无穷间断点和振荡间断点都属于第二类间断点.
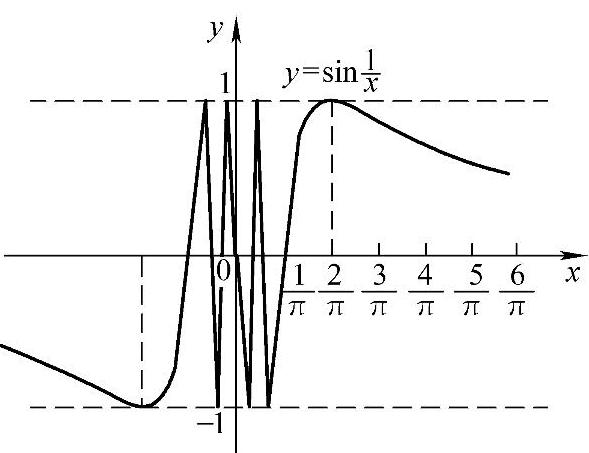
图1-20
三、连续函数的运算性质
定理1.17 若函数f（x）与g（x）都在点x0连续，则函数f±g、f·g、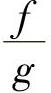
（当g（x0）≠0时）在x0也连续.
此定理可由函数在某点连续的定义和极限的四则运算法则证明，留与读者.
定理1.18 连续函数的复合函数是连续的.
证 设函数u=φ（x）在x0连续，且u0=φ（x0），而函数y=f（u）在u0连续，即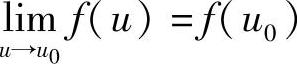
.则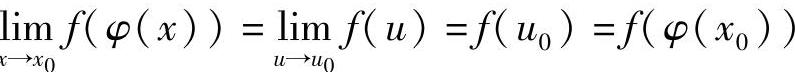
.
故复合函数y=f（φ（x））在点x0连续.
同样可以证明，基本初等函数在其定义区间内是连续的.进而可以证明一切初等函数在其定义域内都是连续的.这样，利用函数的连续性就可以直接代值来求函数的极限.
例9 求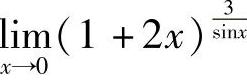
.
解 利用函数连续性及等价无穷小代换，得
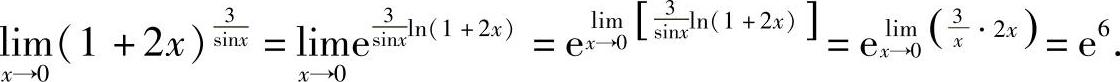
例10 求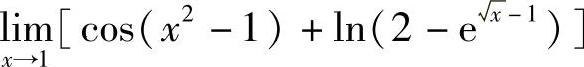
.
解 利用函数连续性，得
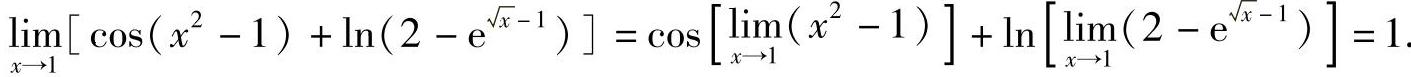
四、闭区间上连续函数的性质
定理1.19 （有界性定理）若函数f（x）在闭区间[a，b]上连续，则它在[a，b]上有界.即存在K＞0，对于任意给定的x∈[a，b]，有|f（x）|≤K.
一般来说，开区间上的连续函数不一定有界.例如，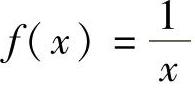
在（0，1）上连续，但它无界.
定理1.20 （最值定理）若函数f（x）在闭区间[a，b]上连续，则f（x）在[a，b]上必有最小值和最大值.即在[a，b]上至少有一点ξ1，使f（ξ1）是f（x）在[a，b]上的最小值；又至少有一点ξ2，使f（ξ2）是f（x）在[a，b]上的最大值（见图1-21），即f（ξ1）≤f（x）≤f（ξ2）.
如图1-21所示，函数f（x）在闭区间[a，b]上连续，f（ξ1）是f（x）在[a，b]上的最小值，f（ξ2）是最大值.达到最小值和最大值的点有可能是闭区间的端点，并且这样的点未必是唯一的.
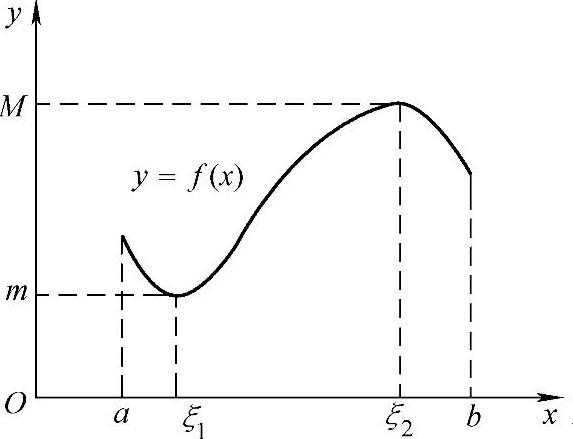
图1-21
开区间内连续的函数不一定有此性质.如函数f（x）=tanx在区间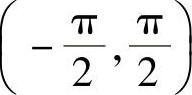
内连续，但
，
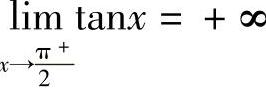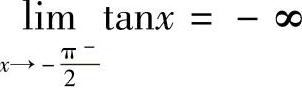，所以f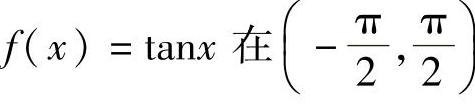
内取不到最值.
同样地，若函数在闭区间上有间断点，也不一定有此性质.如函数
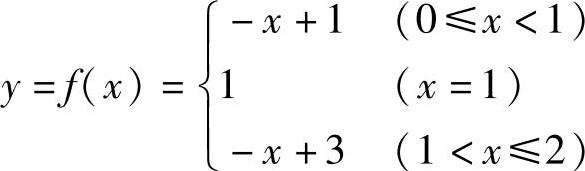
在闭区间[0，2]上有一间断点x=1，函数f（x）虽然在闭区间上有界，但它取不到最大值和最小值（见图1-22）.
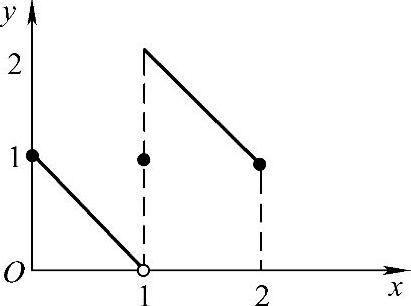
图1-22
定理1.21 （零点定理）若函数f（x）在闭区间[a，b]上连续，且f（a）与f（b）异号，则在（a，b）内至少存在一点ξ，使得f（ξ）=0.这里的ξ称为函数的零点.
其几何意义如图1-23所示，在闭区间[a，b]上定义的连续曲线y=f（x）在两个端点a与b的图像分别在x轴的两侧，则此连续曲线与x轴至少有一个交点，交点的横坐标即ξ.
定理1.21也可表述如下：若f（x）是闭区间[a，b]上的连续函数，且f（a）与f（b）异号，则方程f（x）=0在（a，b）内至少有一个根.
例11 判断方程x3-6x+2=0的根的位置.
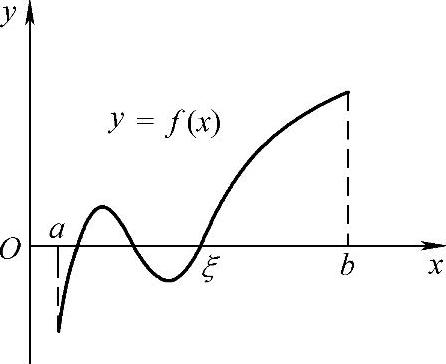
图1-23
解 设f（x）=x3-6x+2，则f（x）在（-∞，+∞）连续.
f（-3）=-7＜0，f（-2）=6＞0，f（-1）=7＞0，f（0）=2＞0，f（1）=-3＜0，f（2）=-2＜0，f（3）=11＞0.
根据零点定理，方程在（-3，-2）、（0，1）和（2，3）内各至少有一个根.又因为该方程为三次方程，至多有三个根，因此在区间（-3，-2）、（0，1）和（2，3）内，方程x3-6x+2=0各有一个根.
定理1.22 （介值定理）若函数f（x）在闭区间[a，b]上连续，M与m分别是f（x）在[a，b]上的最大值和最小值，c是M与m间的任意实数（即m≤c≤M），则在[a，b]上至少存在一点ξ，使得f（ξ）=c（见图1-24）.
证 若m=M，则函数f（x）在[a，b]上是常数，定理显然成立.
若m<M，则在闭区间[a，b]上必存在两点x1和x2，使得f（x1）=M，f（x2）=m，不妨设x1＜x2.
作辅助函数φ（x）=f（x）-c，则φ（x）在[a，b]上连续，且φ（x1）=f（x1）-c＞0，φ（x2）=f（x2）-c＜0.
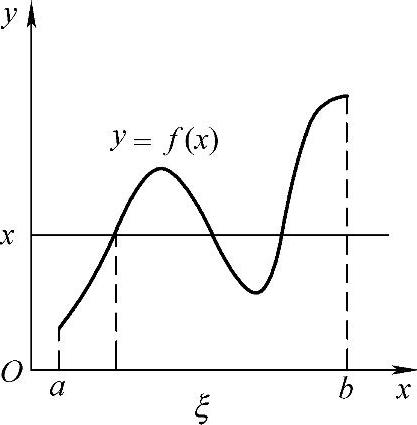
图1-24
由零点定理，在区间（x1，x2）内至少存在一点ξ，使得φ（ξ）=f（ξ）-c=0，即f（ξ）=c（a＜ξ＜b）.
例12 设f（x）在[a，b]上连续，且a＜x1＜x2＜…＜xn＜b，c1，c2，…，cn为任意正实数，则必存在ξ∈[a，b]，使得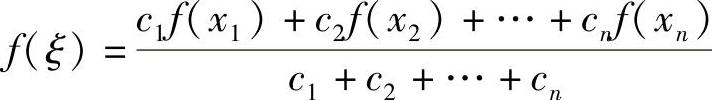
.
解 因为f（x）在[a，b]上连续，则在[a，b]上必存在最小值m和最大值M，从而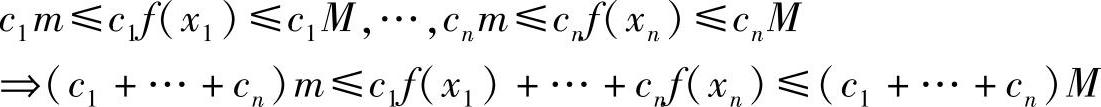
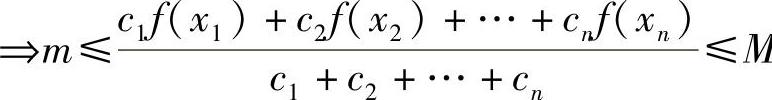.由介值定理，必存在ξ∈[a，b]，使得
