函数的极限
从上一节可知,数列是特殊的极限,极限的实质就是自变量变化时,函数值的变化趋势,那么一般函数的极限又如何呢?
一、当x→∞时,函数f(x)的极限
1.x→+∞时
设函数f定义在[a,+∞)上,类似于数列情形,研究当自变量x趋于+∞时,对应的函数值也能否无限地接近于某个定数A.例如,对于函数
如图1-5所示,当x无限增大时,函数值无限地接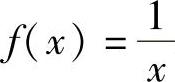 .
.
如图1-5所示,当x无限增大时,函数值无限地接近于0.
图1-5
函数f(x)(x→+∞)的极限定义与数列{xn}的极限定义很相似.这是因为它们的自变量的变化趋势相同(x→+∞与n→+∞).
定义1.13 设函数f(x)在区间(a,+∞)有定义,A是常数.若对于任意给定的正数ε>0,总存在X>0,当x>X时,有|f(x)-A|<ε,则称函数f(x)当x→+∞时以A为极限,表示为
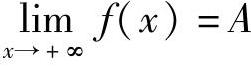 或f(x)→A(当x→+∞).
或f(x)→A(当x→+∞).
在定义中正数X的作用与数列极限定义中的N相似,表明x充分大的程度;但这里所考虑的是比X大的所有实数x,而不仅仅是正整数N.因此,当x趋于正无穷大时函数f(x)以A为极限意味着:A的任意小邻域内必含有f(x)在+∞的某邻域内的全部函数值.
几何意义
几何意义如图1-6所示.
对于任意给定的ε>0,在坐标平面上作两条平行于x轴的直线y=A+ε与y=A-ε,围成以直线y=A为中心线、宽为2ε的带形区域;定义中的“当x>X时,有|f(x)-A|<ε”表示:在直线x=X的右方,曲线y=f(x)全部落在这个带形区域之内.如果正数ε取的再小一点,即当带形区域更窄时,那么直线x=X一般要往右平移;但无论带形区域如何窄,总存在这样的正数X,使得曲线y=f(x)在直线x=X的右边部分全部落在这更窄的带形区域内.
与定义1.13相仿,得到
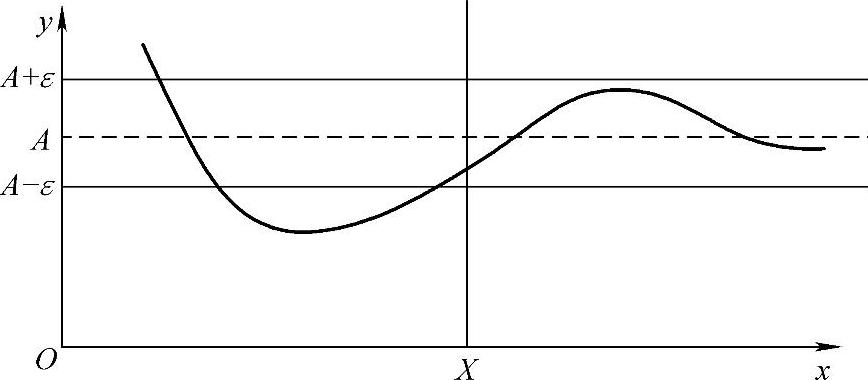
图1-6
2.x→-∞时
定义1.14设函数f(x)在区间(-∞,a)有定义,A是常数,若对于任意给定的ε>0,存在X>0,当x<-X时,有|f(x)-A|<ε,则称函数f(x)当x→-∞时以A为极限,表示为
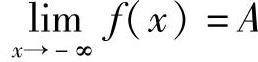 或f(x)→A(当x→-∞).
或f(x)→A(当x→-∞).
3.x→∞时
定义1.15 设函数f(x)在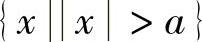 有定义,A是常数,若对于任意给定的ε>0,存在X>0,当x满足|x|>X时,有|f(x)-A|<ε,则称函数f(x)当x→∞时以A为极限,表示为
有定义,A是常数,若对于任意给定的ε>0,存在X>0,当x满足|x|>X时,有|f(x)-A|<ε,则称函数f(x)当x→∞时以A为极限,表示为
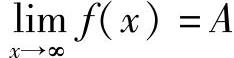 或f(x)→A(当x→-∞).
或f(x)→A(当x→-∞).
例1 证明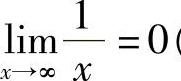 (见图1-7).
(见图1-7).
证 对于任意给定的ε>0,取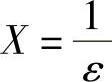 ,则
,则
当|x|>X时有
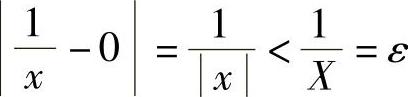
所以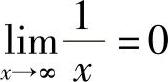 .
.
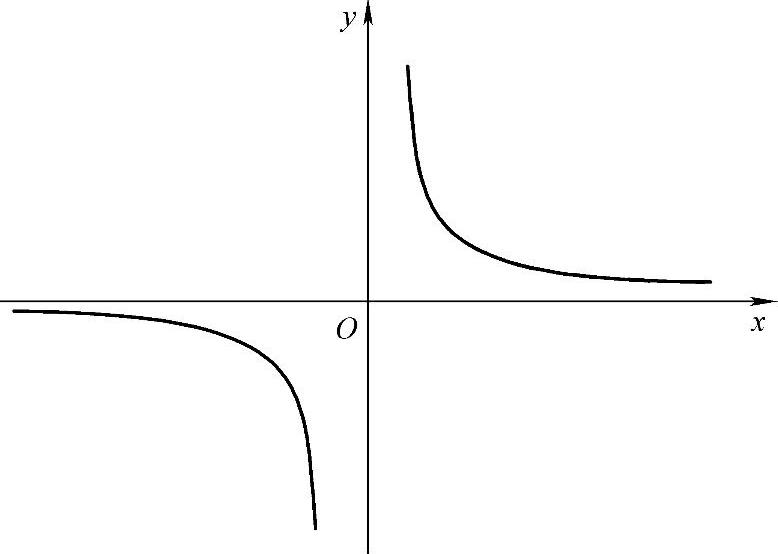
图1-7
例2 证明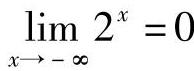 .
.
证 对于任意的ε>0,要使|2x-0|=2x<ε成立,只要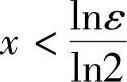 就可以了(这里不妨设ε<1),取
就可以了(这里不妨设ε<1),取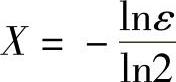 ,于是对于任意的ε>0,存在
,于是对于任意的ε>0,存在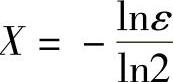 ,当x<-X时,有|2x-0|<ε,即
,当x<-X时,有|2x-0|<ε,即
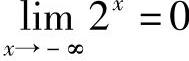
例3 证明(1)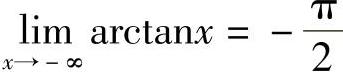 ;(2)xlim
;(2)xlim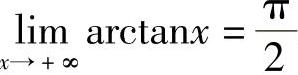 .
.
证 (1)对于任意给定的ε>0,由于

等价于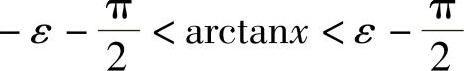 ,而此不等式的左半部分对任何x都成立,所以只要考察其右半部分x的变化范围.
,而此不等式的左半部分对任何x都成立,所以只要考察其右半部分x的变化范围.
为此,不妨设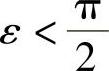 ,则有
,则有
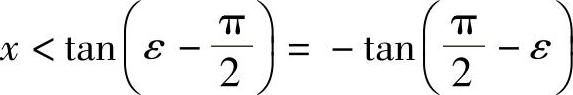
故对任意给定的正数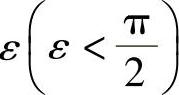 ,只须取
,只须取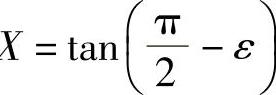 ,则当x<-X时便有式(1-1)成立.这就证明了(1),类似地可证(2).
,则当x<-X时便有式(1-1)成立.这就证明了(1),类似地可证(2).
综合(1)、(2)由定义可知,当x→∞时函数arctanx不存在极限.
二、当x→x0时,函数f(x)的极限
考察函数f(x)=2x+1.当x趋于2时,可以看到它所对应的函数值就趋于5(见图1-8).
考察函数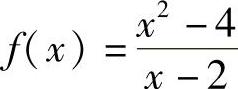 .当x≠2时,f(x)=x+2,由此可见,当x不等于2而趋于2时,对应的函数值f(x)就趋于4(见图1-9).
.当x≠2时,f(x)=x+2,由此可见,当x不等于2而趋于2时,对应的函数值f(x)就趋于4(见图1-9).
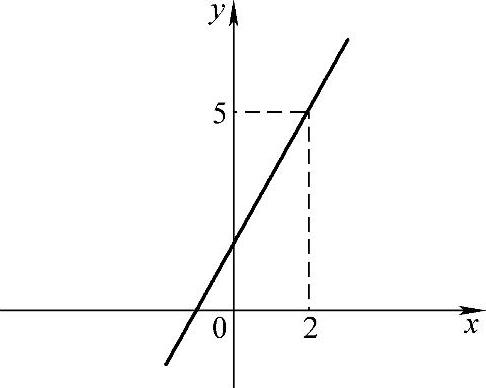
图1-8
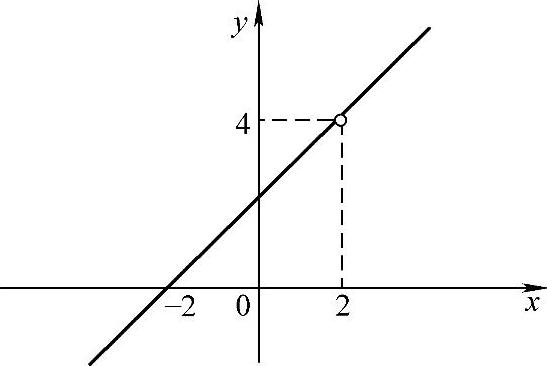
图1-9
不难看出,上述两个例子和上段中当x→∞时极限存在的情形相似,而这里是“当x趋于x0(但不等于x0)时,对应的函数值f(x)就趋于某一确定的数A”.
定义1.16 设函数f(x)在x0的某个去心邻域内有定义,A是常数,若对于任意给定的正数ε>0,总存在正数δ>0,使得x满足不等式|0<x-x0|<δ时,有
|f(x)-A|<ε
则称函数f(x)当x→x0时以A为极限,表示为
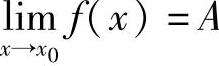 或f(x)→A(当x→+∞).
或f(x)→A(当x→+∞).
在此极限定义中,“0<|x-x0|<δ”指出x≠x0,这说明函数f(x)在x0的极限与它在x0处的定义和取值无关.x0既可以不在函数f(x)的定义域内;又可以在函数f(x)的定义域内,但这时函数f(x)在x0的极限与f(x)在x0的函数值f(x0)可以没有任何联系.
几何意义
“ε-δ”定义表明,任意做一条以直线y=A为中心线,宽为2ε的横带(无论怎样窄),必存在一条以x=x0为中心,宽为2δ的直带,使直带内的函数图像全部落在横带内(见图1-10).
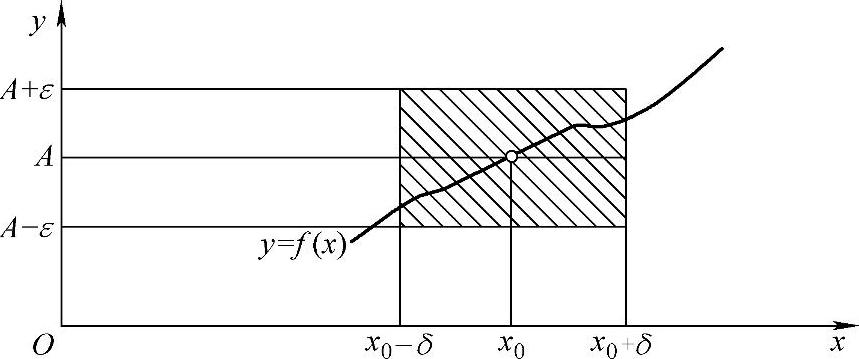
图1-10
例4 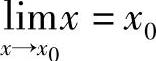 .
.
证 由于|f(x)-A|=|x-x0|,因此对于任意给定的正数ε,可取正数δ=ε,当0<|x-x0|<δ时,不等式|f(x)-A|=|x-x0|<ε成立.
所以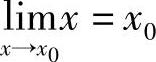 .(https://www.daowen.com)
.(https://www.daowen.com)
例5 设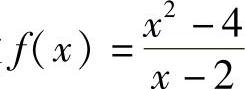 ,证明
,证明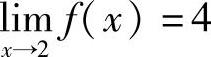 .
.
证 由于当x≠2时,|f(x)-4|=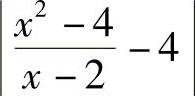 =x-2
=x-2
,故对任意给定的ε>0,只要取δ=ε,则当0<|x-2|<δ时有|f(x)-4|<ε.这就证明了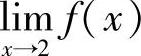 =4.
=4.
例6 证明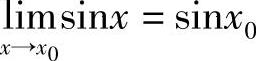 .
.
证 先建立一个不等式,即当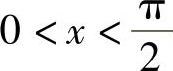 时有
时有
sinx<x<tanx (1-2)
事实上,在如图1-11所示的单位圆(半径为1)内,当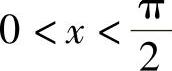 时,sinx=CD,
时,sinx=CD,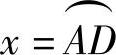 ,tanx=AB,所以
,tanx=AB,所以
S△OAD<S扇形OAD<S△OAB,
即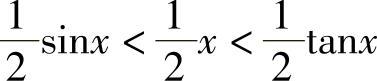 ,由此立得式(1-2).
,由此立得式(1-2).
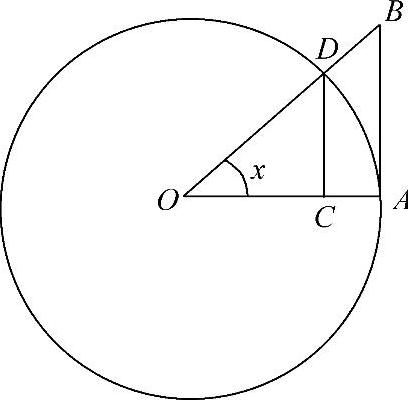
图1-11
又因为当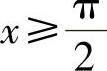 时,有sinx≤1<x,故对一切x>0都有sinx<x;
时,有sinx≤1<x,故对一切x>0都有sinx<x;
当x<0时,由sin(-x)<-x得-sinx<-x.综上所述,又得到不等式
|sinx|<|x|,(x∈R) (1-3)
由此,从式(1-3)得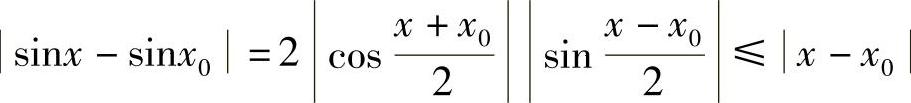 .对于任意给定的ε>0,只要取δ=ε,则当0<|x-x0|<δ时,就有|sinx-sinx0|<ε.所以
.对于任意给定的ε>0,只要取δ=ε,则当0<|x-x0|<δ时,就有|sinx-sinx0|<ε.所以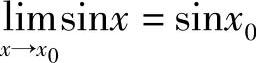 .
.
单侧极限 有些函数在其定义域上某些点的左侧与右侧解析式不同(如分段函数定义域上的某些点),或函数在某些点仅在其一侧有定义(如在定义区间端点处),这时函数在那些点上的极限只能单侧地给出定义,称之为单侧极限.
例如,函数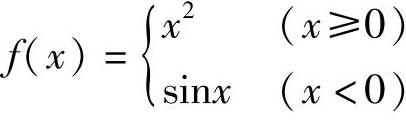
当x>0而趋于0时,应按f(x)=x2来考察函数值的变化趋势;当x<0而趋于0时,应按f(x)=sinx来考察.又如函数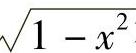 在其定义区间[-1,1]端点x=±1处的极限,也只能在点x=-1的右侧和点x=1的左侧来分别讨论.,
在其定义区间[-1,1]端点x=±1处的极限,也只能在点x=-1的右侧和点x=1的左侧来分别讨论.,
定义1.17 设函数f(x)在x0的左邻域(或右邻域)有定义,A是常数.若对于任意给定的ε>0,存在δ>0,当x满足x0-δ<x<x0(或x0<x<x0+δ)时,有
|f(x)-A|<ε则称A是函数f(x)在x0的左极限(或右极限).记作
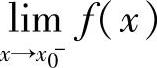 =A或f(x0-0)=A,
=A或f(x0-0)=A,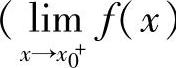 =A或f(x0+0)=A).
=A或f(x0+0)=A).
左极限与右极限统称为单侧极限.它们与极限的关系,有下述定理.
定理1.5 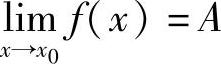 的充要条件是
的充要条件是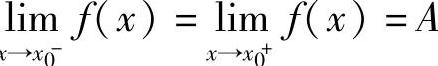 .类似有
.类似有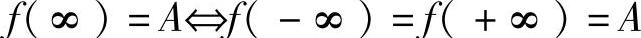 .
.
例7 设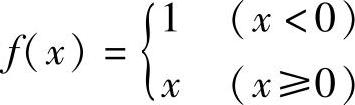 ,研究当x趋于0时,f(x)的极限是否存在.
,研究当x趋于0时,f(x)的极限是否存在.
解 当x<0时,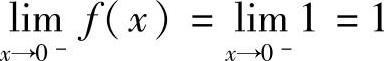 ,而当x>0时,
,而当x>0时,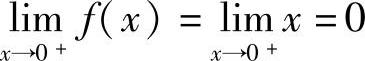 .
.
左、右极限都存在但不相等,所以,由定理1.5可知当x→0时,f(x)不存在极限(见图1-12).
例8 研究当x→0时,f(x)=x的极限.
解 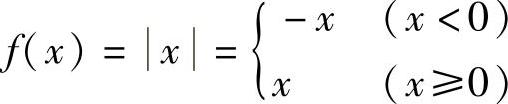 .
.
因为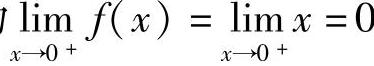 ,
,
所以,由定理1.5可得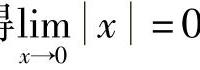 .
.
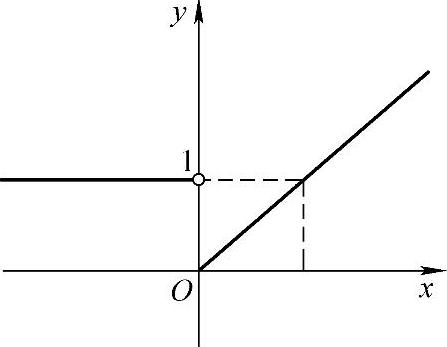
图1-12
三、函数极限的性质
在此节中,引入了下述六种类型的函数极限:
(1)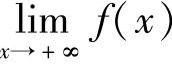 ;(2)
;(2)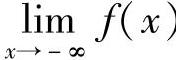 ;(3)
;(3)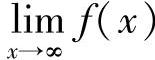 ;(4)
;(4)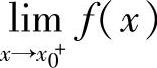 ;(5)
;(5)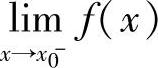 ;(6)
;(6)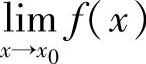 .
.
它们具有与数列极限相类似的一些性质,以后都以第(6)种类型的极限为代表来叙述并证明这些性质.至于其他类型极限的性质及其证明,只要相应的做些修改即可.
1.极限唯一性
定理1.6 若极限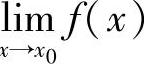 存在,则此极限是唯一的.
存在,则此极限是唯一的.
证 设A、B都是f当x→x0时的极限,则对任意给定的ε>0,分别存在正数δ1与δ2,使得当0<|x-x0|<δ1时,有

当0<|x-x0|<δ2时,有
|f(x)-B|<ε (1-5)
取δ=min(δ1,δ2),则当0<|x-x0|<δ时,式(1-4)与式(1-5)同时成立,故有
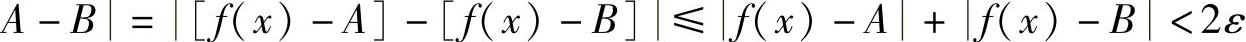
由ε的任意性得A=B.这就证明了极限是唯一的.
2.局部有界性
定理1.7 若极限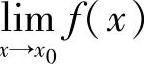 存在,则f在x0某去心邻域
存在,则f在x0某去心邻域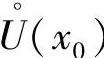 内有界.
内有界.
证 设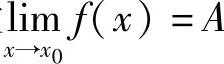 .取ε=1,则存在δ>0,使得对一切
.取ε=1,则存在δ>0,使得对一切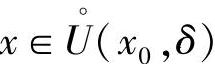 有
有
|f(x)-A|<1
即|f(x)|≤|f(x)-A+A|<|A|+1.
这就证明了f在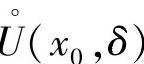 内有界.
内有界.
3.局部保号性
定理1.8 若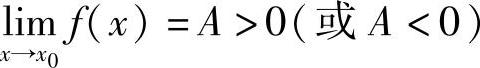 ,则对任何正数r<A(或r<-A),存在
,则对任何正数r<A(或r<-A),存在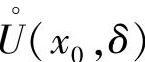 ,使得对一切
,使得对一切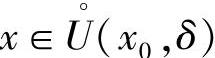 ,有
,有
f(x)>r>0(或f(x)<-r<0)
证 设A>0,对任意r∈(0,A),取ε=A-r,则存在δ>0,使得对一切 (x0,δ),有f(x)>A-ε=r,这就证得结论.对于A<0的情形可类似地证明.
(x0,δ),有f(x)>A-ε=r,这就证得结论.对于A<0的情形可类似地证明.
推论1.2 (保不等式性)设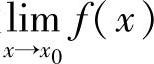 与
与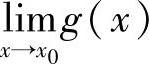 都存在,且在某邻域
都存在,且在某邻域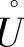 (x0,δ′)内有f(x)≤g(x),则
(x0,δ′)内有f(x)≤g(x),则

证 设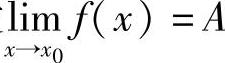 ,
,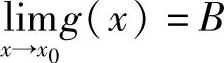 ,则对任意给定的ε>0,分别存在正数δ1与δ2,使得当0<x-x0<δ1时有
,则对任意给定的ε>0,分别存在正数δ1与δ2,使得当0<x-x0<δ1时有
A-ε<f(x) (1-7)
当0<|x-x0|<δ2时有
g(x)<B+ε (1-8)
令δ=min(δ′,δ1,δ2),则当0<|x-x0|<δ时,不等式f(x)≤g(x)与式(1-7)、式(1-8)同时成立,于是有A-ε<f(x)≤g(x)<B+ε,从而A<B+2ε.由ε的任意性得A≤B,即式(1-6)成立.
