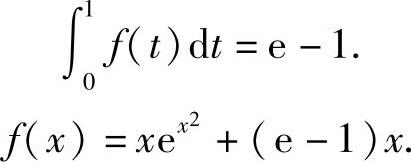微积分基本定理
众所周知，原函数的概念与作为积分和极限的定积分的概念是从两个完全不同的角度引进的，那么它们之间有什么关系呢？本节由引例出发，探讨这两个概念之间的关系，并通过这个关系得出利用原函数计算定积分的公式，即牛顿—莱布尼茨公式.
一、引例
讨论作直线运动的物体的路程函数s（t）与速度函数v（t）之间的关系，一方面，物体从t=a到t=b这段时间所经过的路程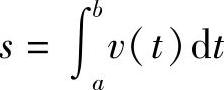
，另一方面
s=s（b）-s（a），
所以
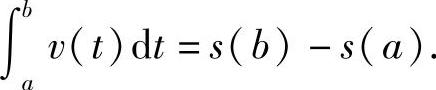
说明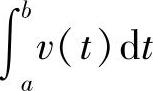
等于v（t）的原函数在区间[a，b]上的增量.
从上节例2的计算结果
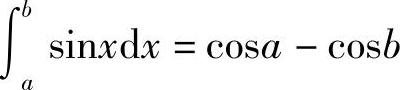
中也可以得到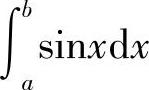
等于sinx的原函数在区间[a，b]上的增量.
为得出一般性的结论，接下来讨论变上限的积分及其重要性质.
二、积分上限函数
定义5.2 设函数f（x）在区间[a，b]上连续，且x为[a，b]上任意一点，则f（x）在区间[a，x]上也连续，定积分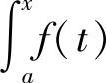
dt存在.于是，对于任意的x∈[a，b]，有唯一确定的
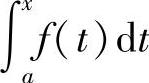与之对应，所以在[a，b]上定义了一个函数，称之为函数f（x）在区间[a，b]上的积分上限的函数，记作Φ（x）（见图5-4），
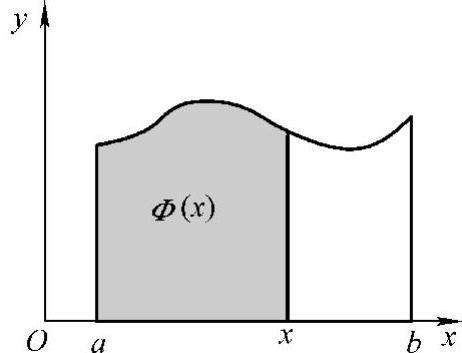
图5-4
即
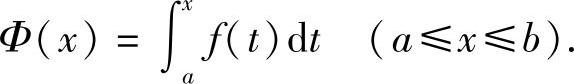
关于积分上限函数的性质，有如下定理.
定理5.4 如果函数f（x）在区间[a，b]上连续，则积分上限的函数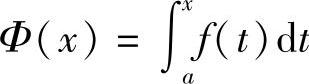
在[a，b]上可导，并且它的导数是
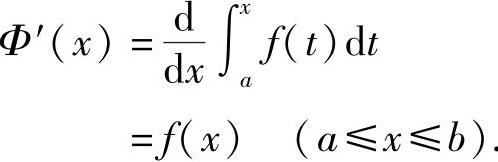
证 设自变量x有增量Δx，使x+Δx∈（a，b），则函数Φ（x）具有增量
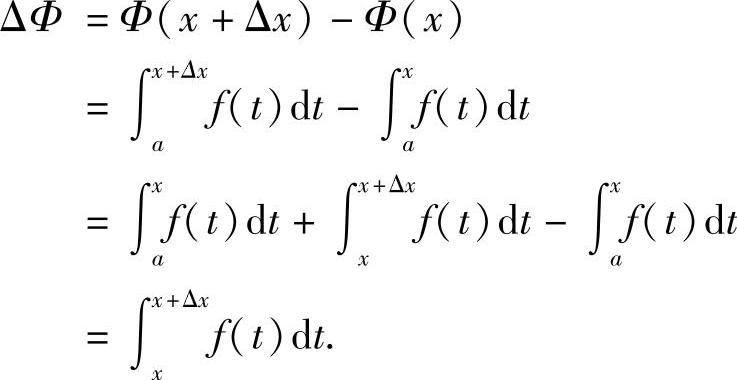
再利用积分中值定理，则有
ΔΦ=f（ξ）Δx，
ξ介于x与x+Δx之间于是，有
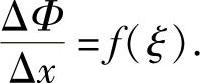
由于f（x）在[a，b]上连续，且当Δx→0时，ξ→x，有
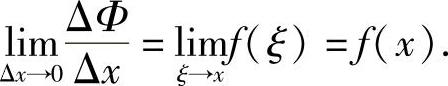
若x=a，取Δx＞0，则同理可证Φ+′（a）=f（a）；若x=b，取Δx＜0，则同理可证Φ-′（b）=f（b）.
推论5.3（原函数存在定理） 若函数f（x）在区间[a，b]上连续，则函数
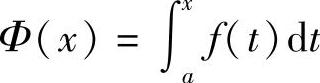
就是f（x）在区间[a，b]上的一个原函数.
推论5.4 设f（x）在[a，b]上连续，u（x），v（x）在[a，b]上可导且
a≤u（x），v（x）≤b，x∈[a，b]，
则
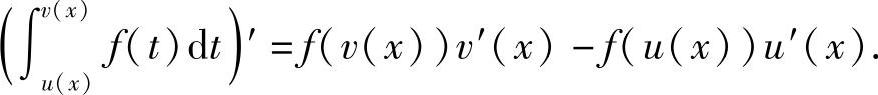
例1 求下列函数的导数：
3）Φ（x）=∫x0f（t）（x-t）dt.
解 1）Φ′（x）=
.
2）Φ′（x）=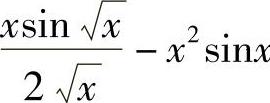
.
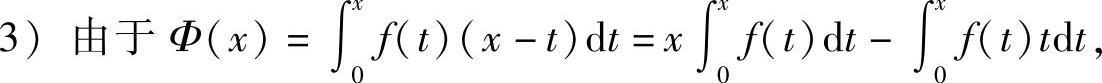
所以
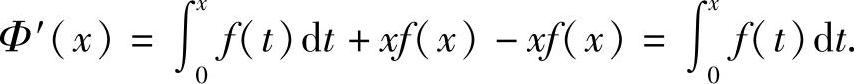
例2 求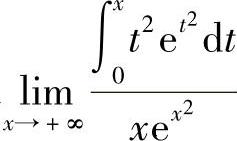
.(https://www.daowen.com)
解 当x>1时，有
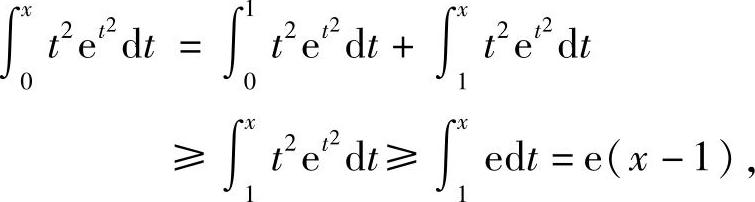
因此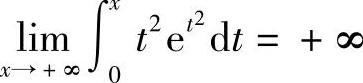
，由洛必达法则，得
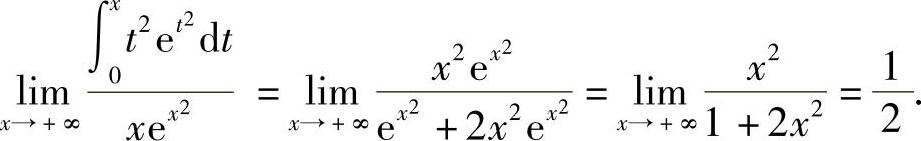
例3 设函数f（x）在区间[a，b]上连续，在（a，b）内可导，且f′（x）≤0，证明
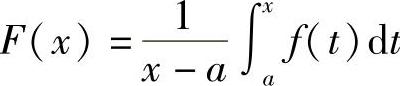
在（a，b）内单调递减.
证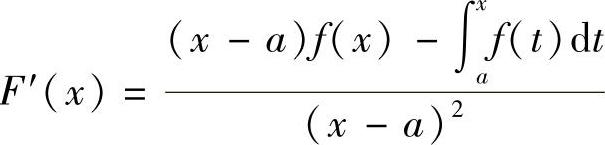 
，因为f（x）在区间[a，b]上连续，由积分中值定理可知存在一点ξ∈（a，x），使得
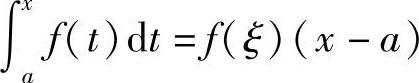
即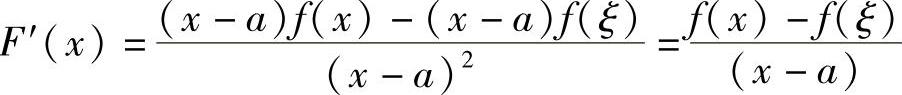
又由f′（x）≤0可知，f（x）在（a，b）内单调递减，
所以
f（x）≤f（ξ）.
从而有F′（x）≤0，即F（x）在（a，b）内单调递减.三、牛顿—莱布尼茨公式
定理5.5 如果函数F（x）是连续函数f（x）在区间[a，b]上的一个原函数，则
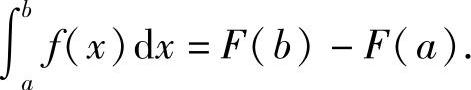
证 已知F（x）是f（x）的一个原函数，积分上限的函数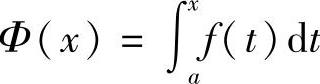
也是f（x）的一个原函数，于是这两个原函数之差F（x）-Φ（x）在[a，b]上必定是某一常数C，即
F（x）-Φ（x）=C（a≤x≤b）.
在上式中，令x=a，则
F（a）-Φ（a）=C.
又
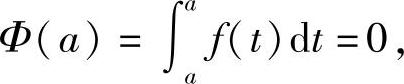
因此C=F（a），因而
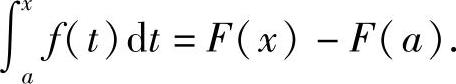
在上式中令x=b，即得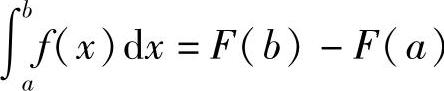
.
有时也写成
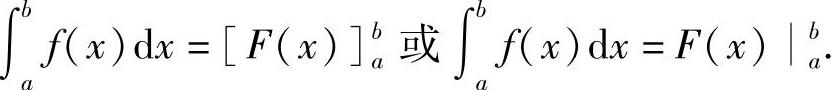
例4 计算定积分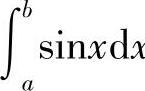
.
解
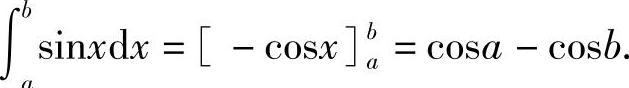
例5 计算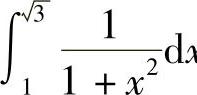
.
解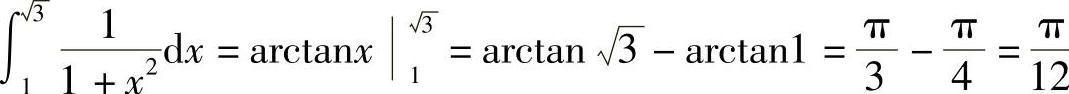 
.
例6 计算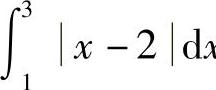
.
解 要去掉绝对值符号，必须分区间积分，显然点x=2为区间的分界点，
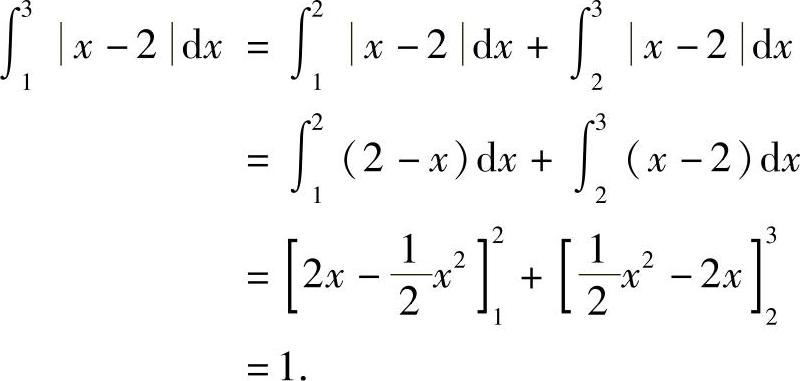
例7 计算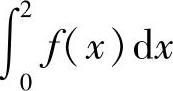
，其中，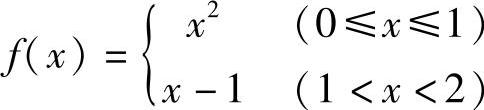
.
解
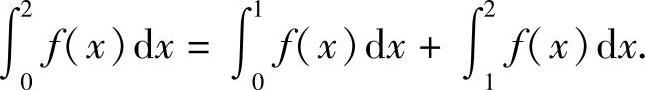
于是
例8 设函数f（x）在区间[0，1]上连续，且满足
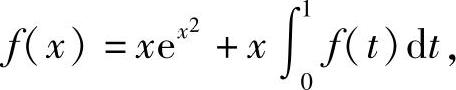
求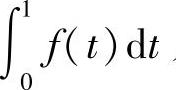
及f（x）.
解
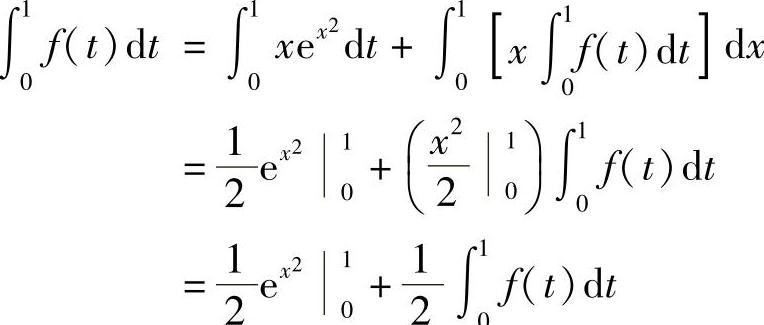
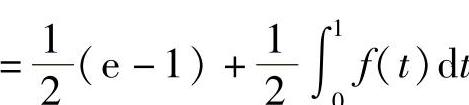,所以
