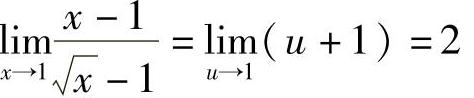极限的运算法则
一、四则运算法则
定理1.9 若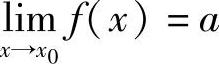 ,
,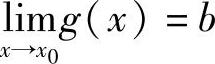 ,则1)
,则1)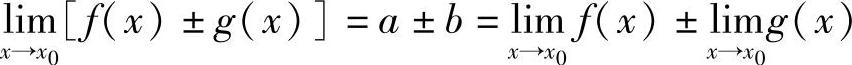 ;2)
;2)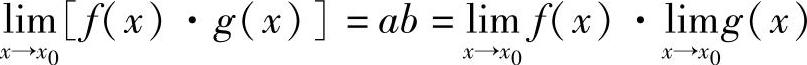 ;3)当b≠0时,
;3)当b≠0时,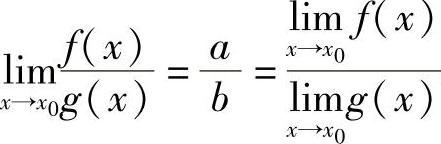 .
.
证 只证2).
因为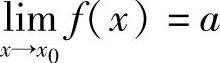 ,存在δ0>0,当0<|x-x0|<δ0时,|f(x)|≤M.
,存在δ0>0,当0<|x-x0|<δ0时,|f(x)|≤M.
对于任意给定的ε>0,存在δ1>0,当0<|x-x0|<δ1时,有f(x)-a<ε成立;
对于任意给定的ε>0,存在δ2>0,当0<|x-x0|<δ2时,有g(x)-b<ε成立;
取δ=min{δ0,δ1,δ2},则当0<|x-x0|<δ时,有
|f(x)·g(x)|-ab=|f(x)·g(x)-f(x)b+f(x)b-ab|≤|f(x)|·|g(x)-b|+|b||f(x)-a|<Mε+|b|ε=(M+|b|)ε
即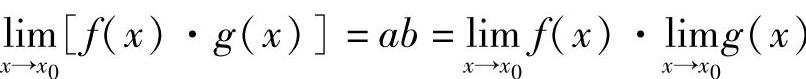 .定理的1)、2)可推广到有限多个函数的和或积的情形.作为2)的特殊情形,有
.定理的1)、2)可推广到有限多个函数的和或积的情形.作为2)的特殊情形,有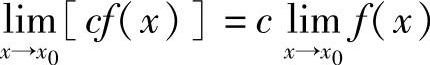 (c为常数),
(c为常数),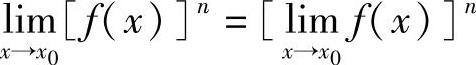 .
.
例1 求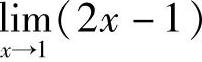 .
.
解 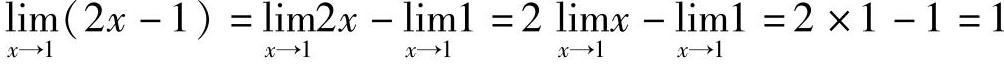 .
.
例2 求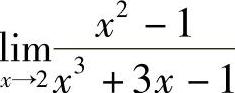 .
.
解 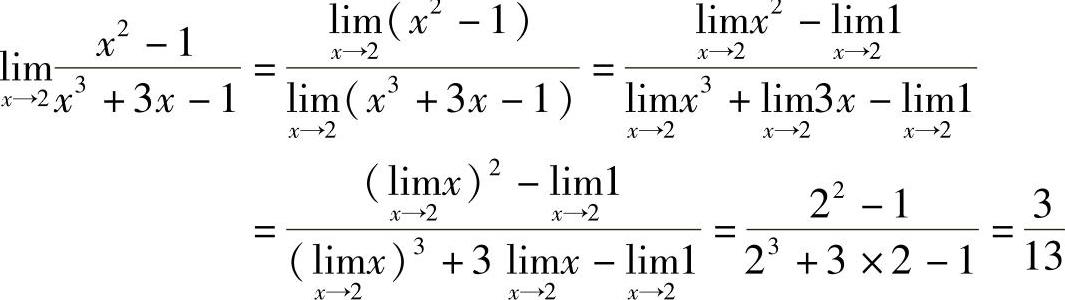 .
.
从例1和例2可以看出,对于有理整函数(多项式)或有理分式函数(分母不为零),求其极限时,只要把自变量x的极限值代入函数就可以了.
对于多项式函数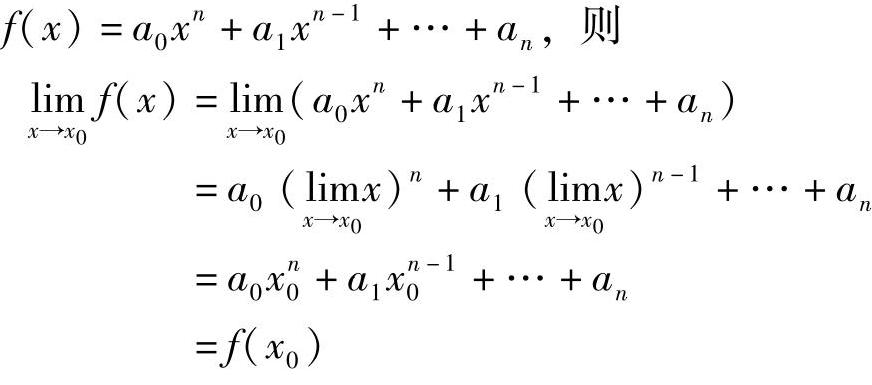
对于有理分式函数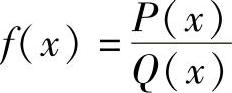 ,其中,P(x)和Q(x)均为多项式,且Q(x0)≠0.
,其中,P(x)和Q(x)均为多项式,且Q(x0)≠0.
则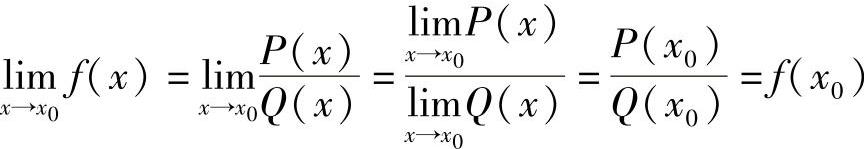 .
.
例3 求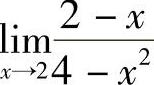 .
.
解 当x→2时,x≠2,x-2≠0.所以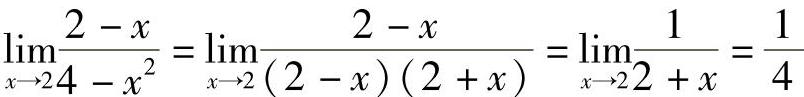 .
.
例4 求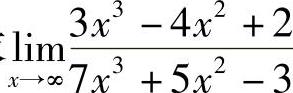 .
.
解 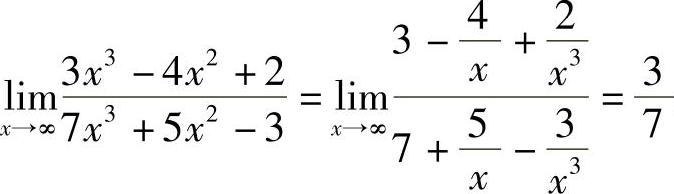 .
.
例5 求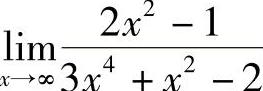 .
.
解 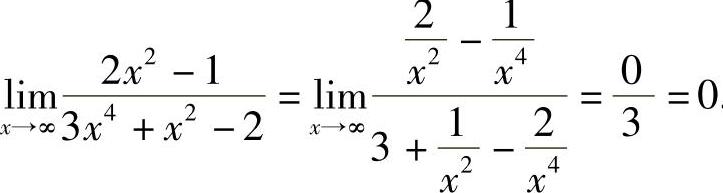 .
.
若Q(x0)=0,则不满足定理条件,不能用上述结论,需采用其他手段.
例6 求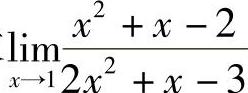 .
.
解 当x→1时,分子、分母均趋于0,因为x≠1,约去公因子(x-1),所以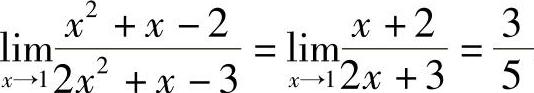 .(https://www.daowen.com)
.(https://www.daowen.com)
例7 求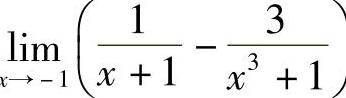 .
.
解 当x→-1时,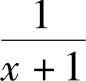 和
和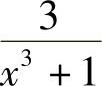 的极限不存在,故不能直接用定理1.9的结论,但当x≠-1时,
的极限不存在,故不能直接用定理1.9的结论,但当x≠-1时,
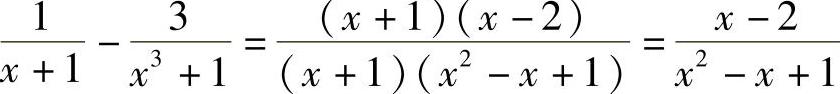
所以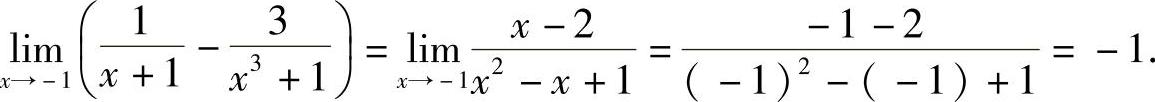
例8 求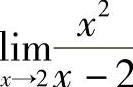 .
.
解 当x→2时,(x-2)→0,故不能直接用定理1.9的结论,由于x2→4,可以考虑: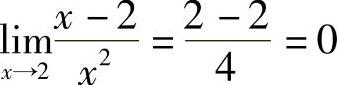 ,由此可知
,由此可知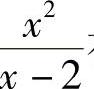 在x→2时,函数值无限增大,把它记为
在x→2时,函数值无限增大,把它记为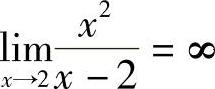 .
.
例9 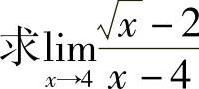 .
.
解 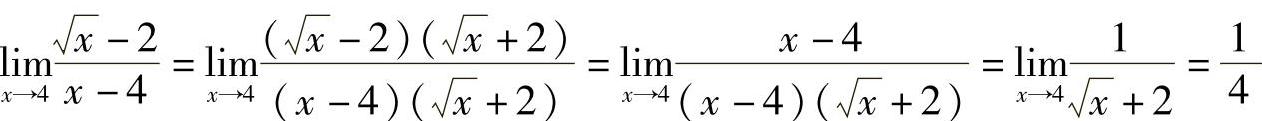 .
.
例10 设a0≠0,b0≠0,m、n为自然数,则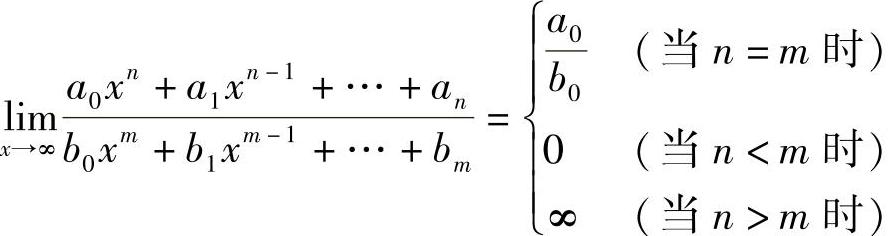
证 当x→∞时,分子、分母极限均不存在,故不能用定理1.9的结论,先变形:.
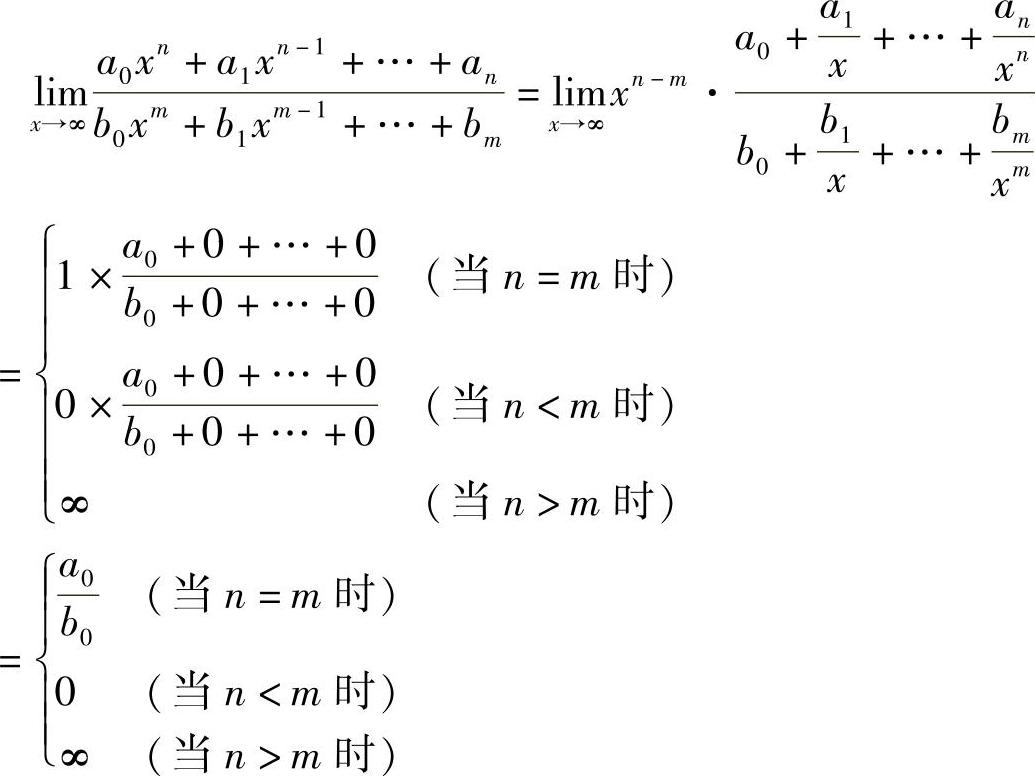
例11 求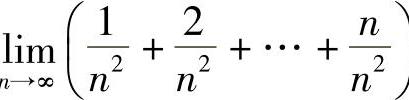 .
.
解 当n→∞时,这是无穷多项相加,故不能直接用定理1.9的结论,先变形: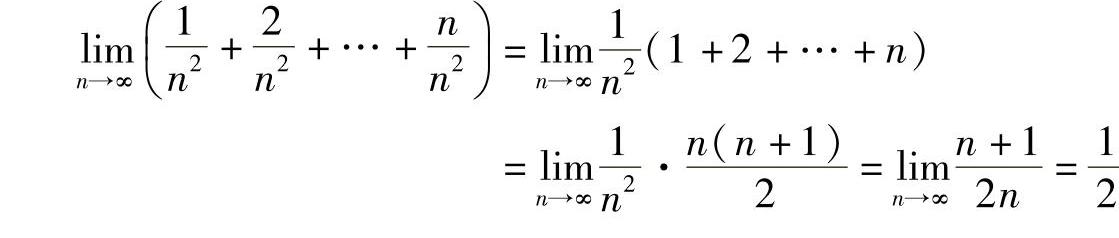 .二、复合函数的极限运算法则
.二、复合函数的极限运算法则
定理1.10 设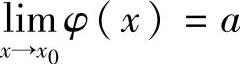 ,且当x满足0<|x-x0|<δ1时,φ(x)≠a,又
,且当x满足0<|x-x0|<δ1时,φ(x)≠a,又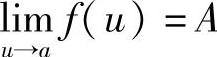 ,则有
,则有
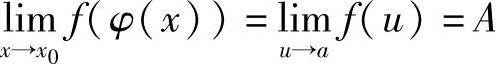
证 由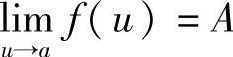 ,对于任意给定的ε>0,存在η>0,当0<u-a<η时,有
,对于任意给定的ε>0,存在η>0,当0<u-a<η时,有
|f(u)-A|<ε
又因为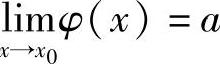 ,则对上述η>0,存在δ2>0,使得当0<|x-x0|<δ2时,有
,则对上述η>0,存在δ2>0,使得当0<|x-x0|<δ2时,有
|φ(x)-a|<η
取δ=min{δ1,δ2},则当0<|x-x0|<δ时,有
0<|φ(x)-a|=|u-a|<η
故|f(φ(x))-A|=|f(u)-A|<ε
结论成立.
若定理中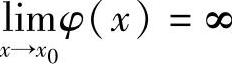 ,类似可证
,类似可证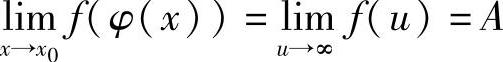 .
.
例12 求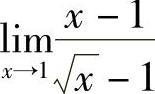 .
.
解 令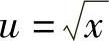 ,则
,则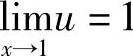 ,从而
,从而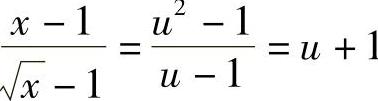 1,故
1,故