数列的极限

第二节 数列的极限

一、数列

通俗地讲，数列就是将一系列的数排成一列（排）.

定义1.11 数列是定义在自然数集上的函数，记为x_n=f（n）n=1，2，3，…

数列的对应值可以按下标从小到大排成一列：x₁，x₂，…，x_n，…，有时也简记为{x_n}或数列x_n.数列中的每一个数称为数列的项，第n项x_n称为一般项或通项.

例1 “一尺之棰，日截其半，万世不竭.”——《庄子·天下篇》

这句话说明，长一尺的棒子，每天截去一半，无限制地进行下去，那么剩下部分的长构成一个数列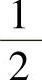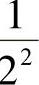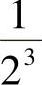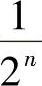：，，，…，，…，通项为.

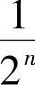例2 2.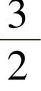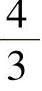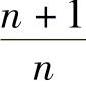，，…；，…；1，3，5，…，2n-1，…；l，-1，1，…，（-1）^n-1，…；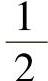

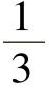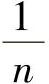1，，，…；，…；1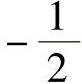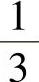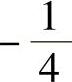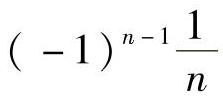，，，，…；a，a，a，…，a,…都是数列.

在数轴上，数列的每项都相应有点与之对应.如果在数轴上依次描出点x_n的位置，能否发现点的位置的变化趋势呢？显然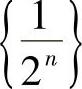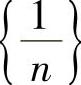，，是无限接近于0的；{2n-1}是无限增大的；{（-1）n-1}的项是在1与-1之间跳动的，不接近于某一常数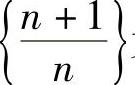；无限接近于常数1.

对于数列来说，最重要的是研究其在变化过程中无限接近某一常数的那种渐趋稳定的状态，这就是常说的数列的极限问题.

二、数列的极限

1.数学描述

若数列{x_n}的极限为a，则意味着当n→∞时，即n无限增大时，x_n无限接近于a，在数学上用距离x_n-a来度量x_n接近a的程度.因为n越大，x_n越接近于a，所以n越大，|x_n-a|越小，所以对任意小的正数ε，存在一个正整数N，当n＞N时，使得|x_n-a|可以小于指定的正数ε.

比如，考察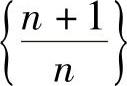的情况.不难发现随着n的增大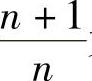，无限地接近于1，即当n充分大时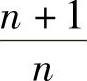，与1可以任意地接近，即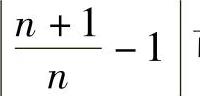可以任意地小，换言之，’ ’

当n充分大时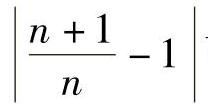，可以小于预先给定的无论多么小的正数ε.

假如取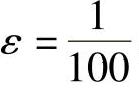，由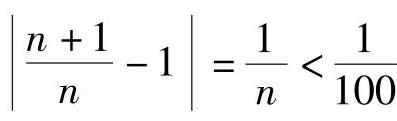，所以n＞100，即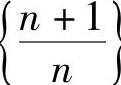}从第101项开始，以后的项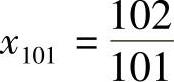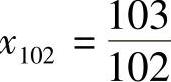，，…都满足不等式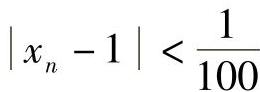，或者说，当n＞100时，有.

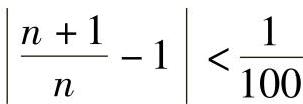同理，若取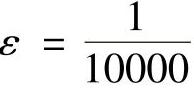，由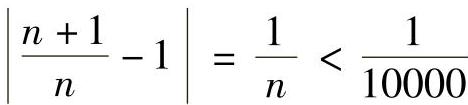，所以n＞10000，即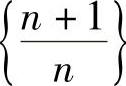从第10001项开始，以后的项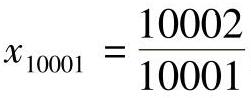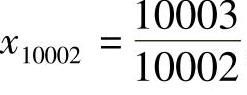，，…都满足不等式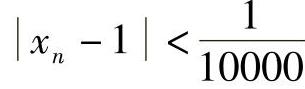，或者说，当n＞10000时，有.

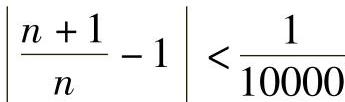一般地，不论给定的正数ε多么小，总存在一个正整数N，当n＞N时，有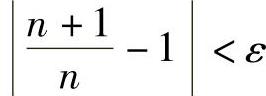.这就充分体现了当n越来越大时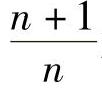，无限接近1这一事实.这个数1称为当n→∞时，数列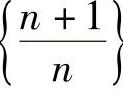的极限.

2.数列极限的定义

定义1.12 设{x_n}是一个数列，a是常数.若对于任意的正数ε（不论ε多么小），总存在一个正整数N，使得当n＞N时，不等式|x_n-a|＜ε恒成立，则称常数a为数列x_n的极限，或称数列x_n收敛于a，记为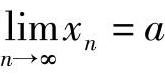或x_n→a（n→∞）.

这时说数列是收敛的，否则称数列是发散的.

例3 证明数列2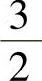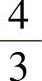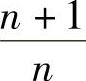，，，…，，…收敛于1.

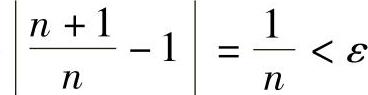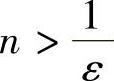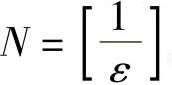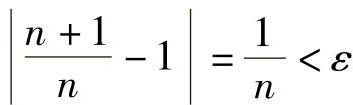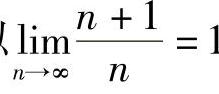证 对于任意ε＞0，要使得成立，只需，所以取，当n＞N时，有，所以1.

这里的N是随ε的变小而变大的，是取决于ε的函数.解题中，只要说明存在一个N，使得当n＞N时，有x_n-a＜ε就行了，而不必求最小的那个N.

例4 证明.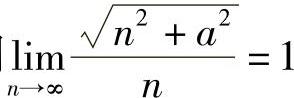

证 对于任意ε＞0，因为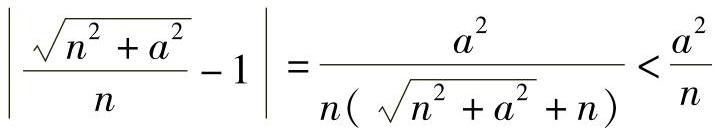

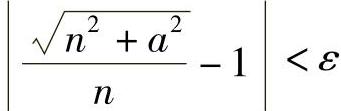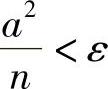所以要使得，只要就行了.

即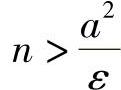

所以取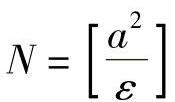，当n＞N时，因为有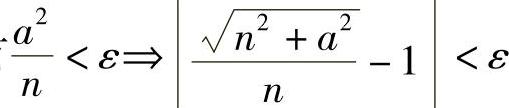，所以.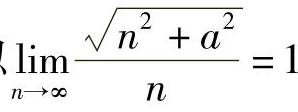

有时找N比较困难，这时可把|x_n-a|适当地变形或放大.

例5 设|q|＜1，试证明数列1，q，q²，…，q^n-1，…的极限为0.

证 若q=0，结论是显然的.

现设0＜|q|＜1，对于任意ε>0（ε越小越好，不妨设ε＜1），要使得|q|^n-1_-0＜ε，即q^n-1＜ε，只须在不等式两边取对数后，使得（n-1）ln|q|＜lnε成立就行了.因为0＜q＜1，所以ln|q|＜0，所以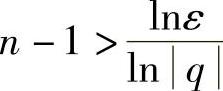，即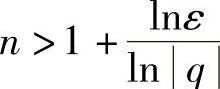.(https://www.daowen.com)

取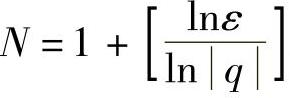，则当n＞N时，有q^n-1-0＜ε成立.

即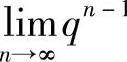=0（q＜1）

3.数列极限的几何意义

由不等式|x_n-a|＜ε等价于a-ε＜x_n＜a+ε.可得到数列极限的几何意义：任意一个邻域U（a，ε），数列中总存在某一项x_N，在此项后面的所有项x_N+1，x_N+2，…，它们在数轴上对应的点，都位于邻域U（a，ε）中（见图1-4）.因为ε＞0可以任意小，所以数列中各项所对应的点x_n都无限聚集在点a附近.

图1-4

三、收敛数列的性质

1.极限唯一性

定理1.2 若数列{x_n}收敛，则它只有一个极限.

证 设a和b为x_n的任意两个极限，下面证明a=b.

由极限的定义，对于任意给定的ε>0，必分别存在自然数N₁，N₂.

当n＞N₁时，有|x_n-a|<ε （1）

当n＞N₂时，有|x_n-b|<ε （2）

令N=max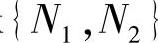，当n＞N时，（1）、（2）两式同时成立.

现考察a-b=（|x_n-b|）-（|x_n-a|）≤|x_n-b|+|x_n-a|＜ε+ε=2ε.

由于a、b均为常数，ε为任意小的正数，所以有a=b，所以x_n的极限只能有一个.

例6 证明数列x_n=（-1）n+1是发散的.

证 反证法：

假设x_n收敛，由极限的唯一性，设.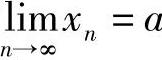

由定义，取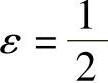，则存在自然数N，当n＞N时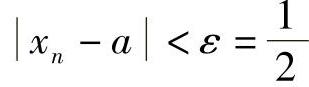，，即

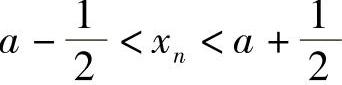
但因为x_n交替取值1与-1，而这两个数不可能同时落在长度为1的开区间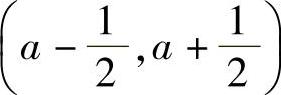内，所以矛盾，故数列x_n=（-1）n+1发散.

2.有界性

定理1.3 若数列{x_n}收敛，那么它一定有界.即存在M＞0，对于任意给定的n都有|x_n|≤M.

证 设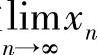=a，由定义取ε=1，存在自然数N，当n＞N时，|x_n-a|＜ε=1，所以当n＞N时，|x_n|≤|x_n-a|+|a|＜1+a，令M=max{|x₁|，|x₂|，…，|x_N|，1+|a|}，显然对一切n都有|x_n|≤M成立.

但是，本定理的逆定理并不成立，即“有界未必收敛”.如数列x_n=（-1）n+1有界，但不收敛.

3.保号性

定理1.4 若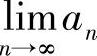=a，且a＞0，则对任意给定的r∈（0，a），存在正整数N，当n＞N时有a_n＞r＞0；若

当n>N时有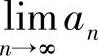=a＜0，则对任意给定的r∈（a，0），存在正整数N，当n＞N时有a_n＜r＜0.

证 第一种情况下，设

时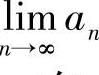=a＞0，取ε=a-r＞0，则存在正整数N，当n＞N时，|a_n-a|＜ε=a-r，有a-（a-r）＜a_n，即a_n＞r＞0.

其余情况，可以类似地证明.

推论1.1 若使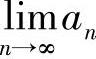=a≠0，则对任意给定的0＜r＜|a|，存在正整数N，当n＞N时，使得|a_n|＞r.