定积分的换元积分法与分部积分法
用牛顿—莱布尼茨公式计算定积分时,需要求出被积函数的原函数,由于用换元积分法和分部积分法可以求出一些函数的原函数,因此,在一定条件下,可以用换元积分法和分部积分法来计算定积分.下面讨论定积分的这两种计算方法.
一、定积分的换元积分法
定理5.6 若函数f(x)在区间[a,b]上连续,函数x=φ(t)在区间[α,β]上具有连续的导数,当t在区间[α,β]上变化时,x=φ(t)的值在[a,b]上变化,且φ(α)=a,φ(β)=b,则
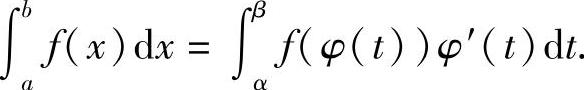
证 设F(x)是f(x)在[a,b]上的一个原函数,则
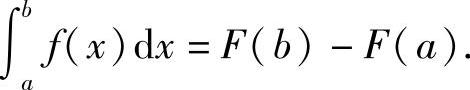
再设Φ(t)=F(φ(t)),对Φ(t)求导,得
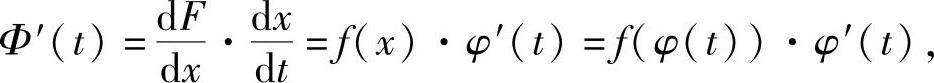
即,Φ(t)是f(φ(t))φ′(t)的一个原函数,因此有
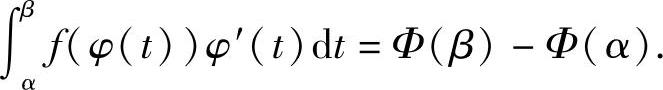
又由Φ(t)=F(φ(t)),φ(α)=a,φ(β)=b,可知
Φ(β)-Φ(α)=F(φ(β))-F(φ(α))=F(b)-F(a),所以
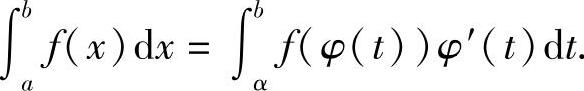
应用换元公式计算定积分应注意两点:1)用x=φ(t)把原来变量x代换成新变量t时,积分限也要换成相应于新变量t的积分限;2)求出f(φ(t))φ′(t)的一个原函数Φ(t)后,不必像计算不定积分那样再把Φ(t)变成原来变量x的函数,而只要把新变量t的上、下限分别代入Φ(t)中然后相减即可.
例1 计算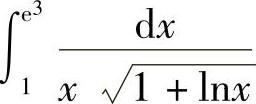 .
.
解 令t=lnx,则x=et,dx=et dt,于是
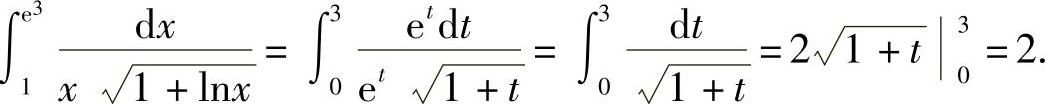
在例1中,如果不明显地写出新变量,那么定积分的上、下限就不要变更.现在用另一种记法计算如下:
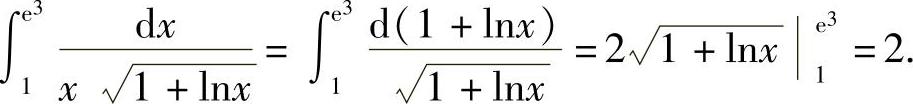
例2 计算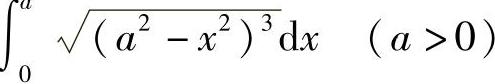 .
.
解 令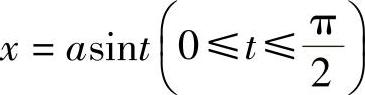 ,则dx=acostdt,当x=0时,t=0;当x=a时,
,则dx=acostdt,当x=0时,t=0;当x=a时,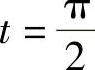 ;于是
;于是
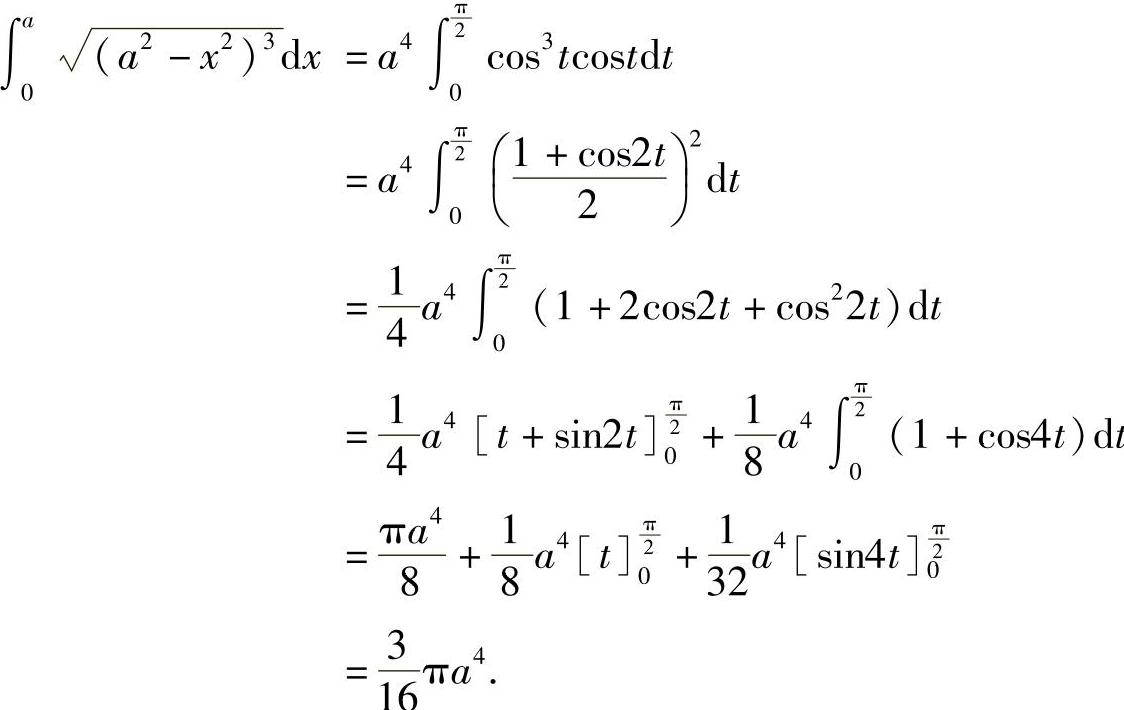
例3 计算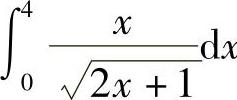 .
.
解 令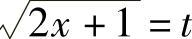 ,则
,则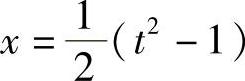 ,dx=tdt,当x=0时,t=1;当x=4时,t=3,于是
,dx=tdt,当x=0时,t=1;当x=4时,t=3,于是
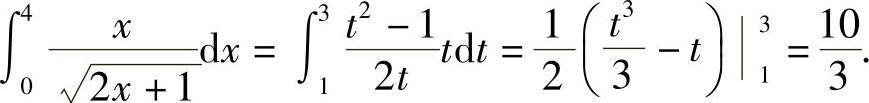
例4 设函数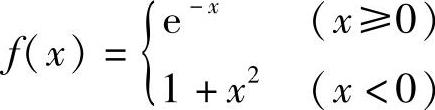 ,求
,求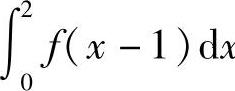 x.
x.
解 令x-1=t,则dx=dt,且当x=0时,t=-1;当x=2时,t=1,于是
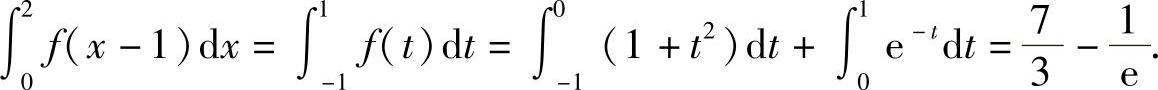
例5 设函数f(x)在[-a,a]上连续,则
1)若f(x)是偶函数,则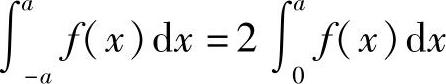 ;2)若f(x)是奇函数,则
;2)若f(x)是奇函数,则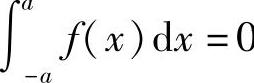 0.
0.
并由此计算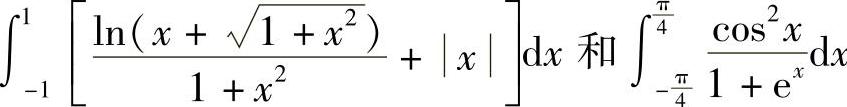 .
.
证 因为
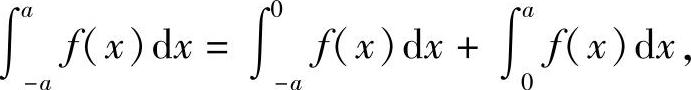
在上式右端第一项中,令x=-t,则有
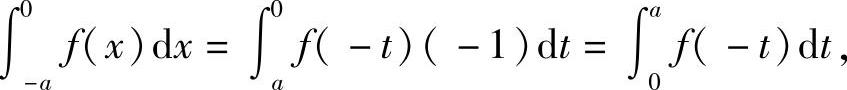
所以
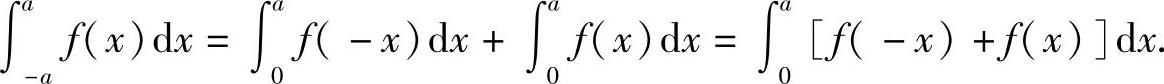
1)当f(x)为偶函数时,f(-x)=f(x),则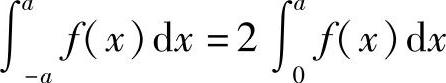 ;2)当f(x)为奇函数时,即f(-x)=-f(x),则
;2)当f(x)为奇函数时,即f(-x)=-f(x),则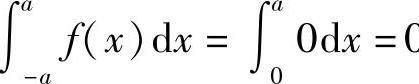 0.
0.
在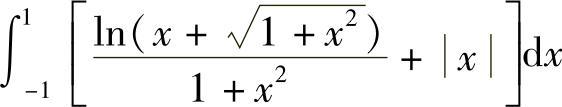 中,因为
中,因为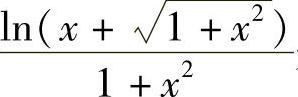 是在[-1,1]上连续的奇函数,x是在[-1,1]上连续的偶函数,所以
是在[-1,1]上连续的奇函数,x是在[-1,1]上连续的偶函数,所以
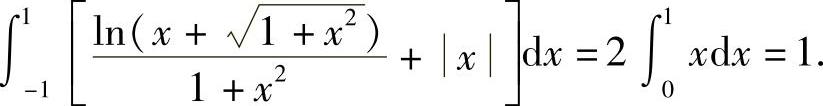
在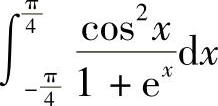 中,由于被积函数的原函数不易求出,但积分区间对称,函数又在该区间上连续,则
中,由于被积函数的原函数不易求出,但积分区间对称,函数又在该区间上连续,则
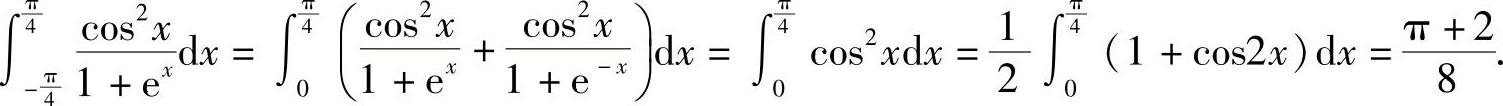
例6 若f(x)在[0,1]上连续,证明: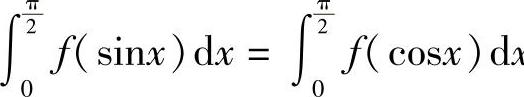 .(https://www.daowen.com)
.(https://www.daowen.com)
证 设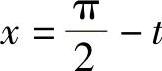 ,则
,则
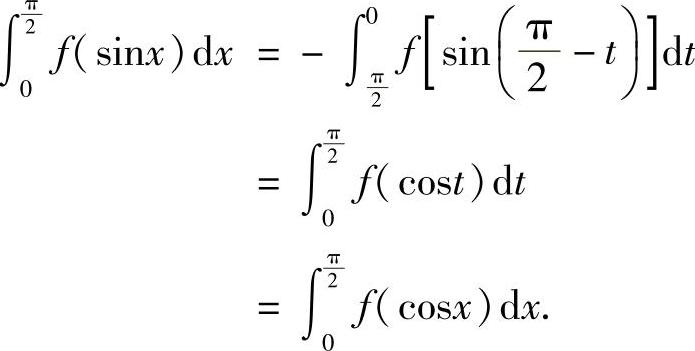
例7 若f(x)在[0,1]上连续,证明: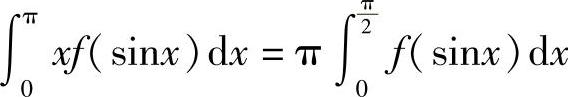 ,并由此计算
,并由此计算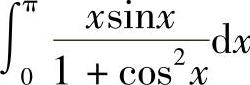 .
.
证 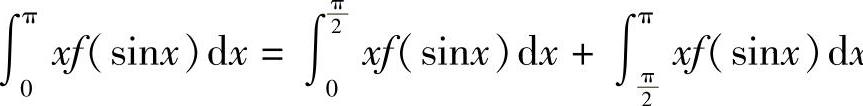 .在上式右端第二项中,设π-x=t,则-dx=dt,
.在上式右端第二项中,设π-x=t,则-dx=dt,
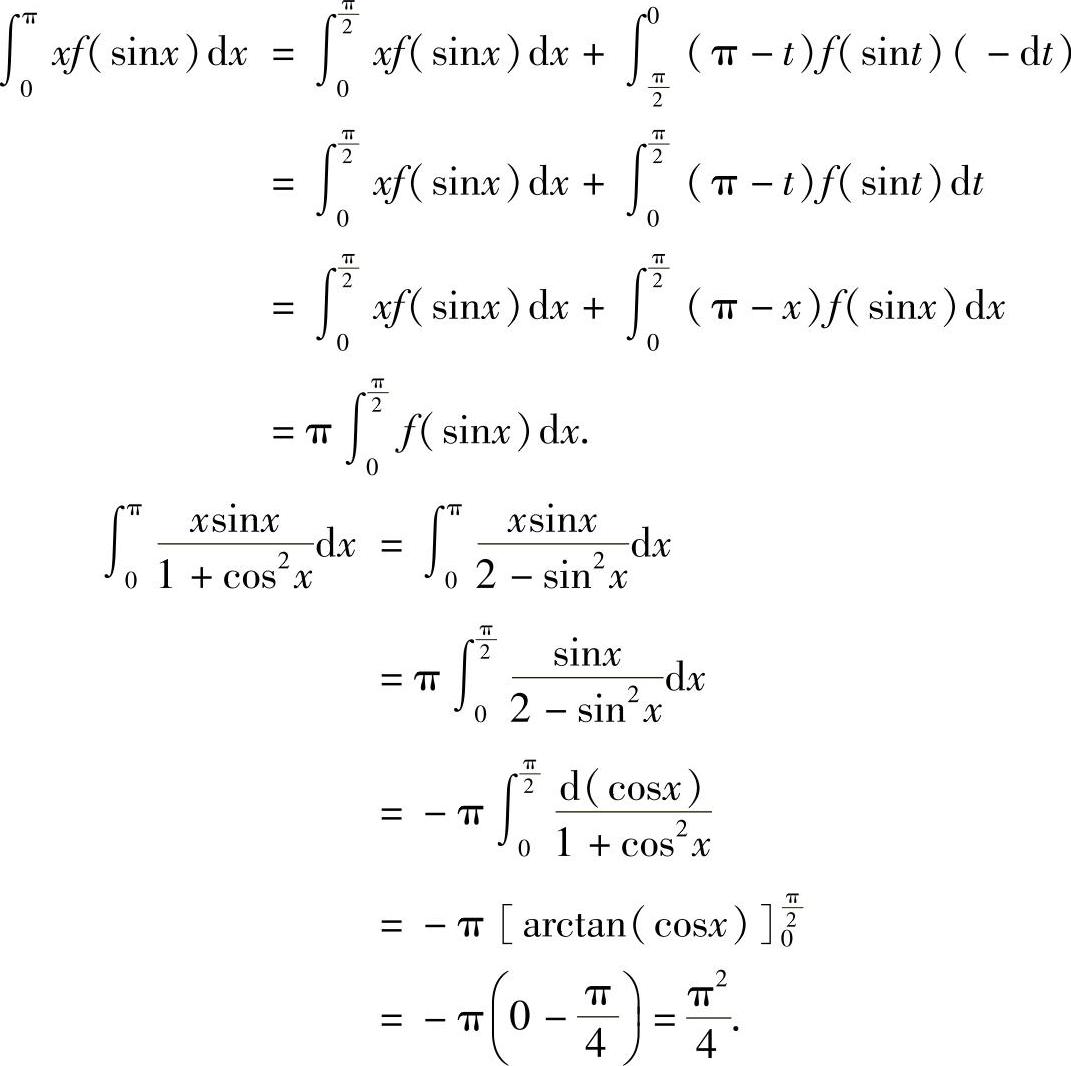
例8 设f(x)是以T(T>0)为周期的周期函数,则对任意常数a,证明:

证
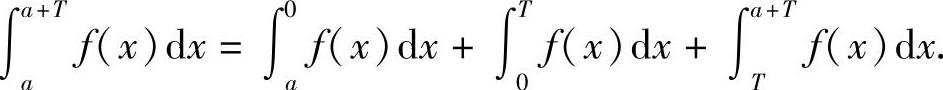
在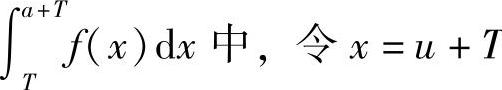 T,则
T,则
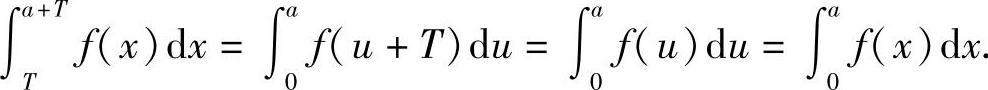
由于
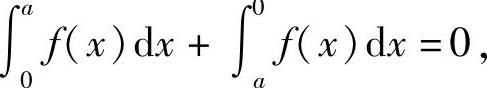
所以
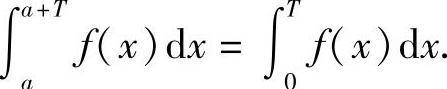
因为sinx是以π为周期的周期函数,所以
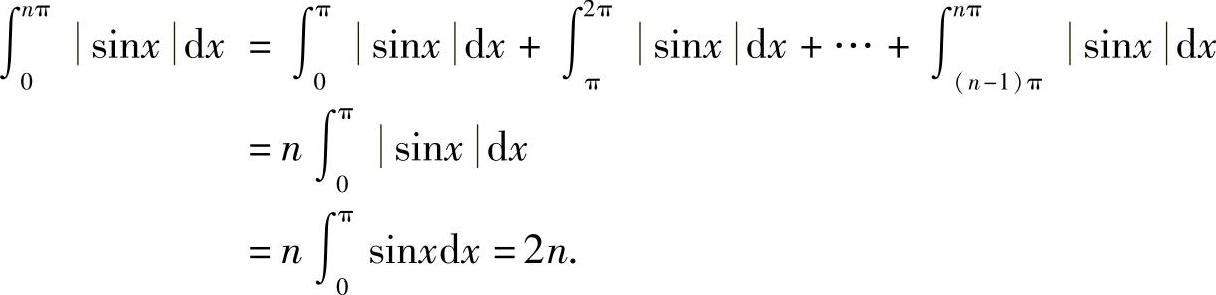
二、定积分的分部积分法
与不定积分的分部积分法类似,有下面的定理.
定理5.7 设u(x)与v(x)在区间[a,b]上连续可导,则有下面的分部积分公式成立
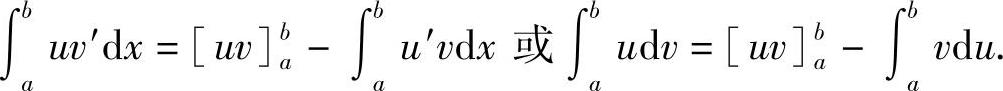
例9 计算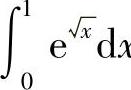 .
.
解 令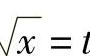 ,则x=t2,dx=2tdt,于是
,则x=t2,dx=2tdt,于是
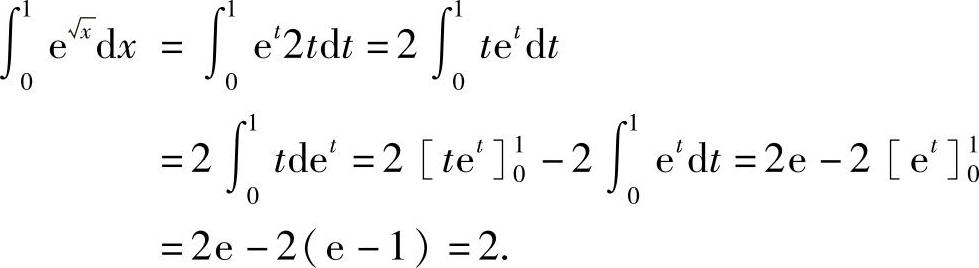
例10 计算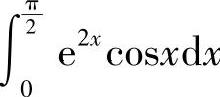 .
.
解 设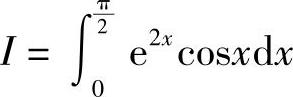 ,则
,则
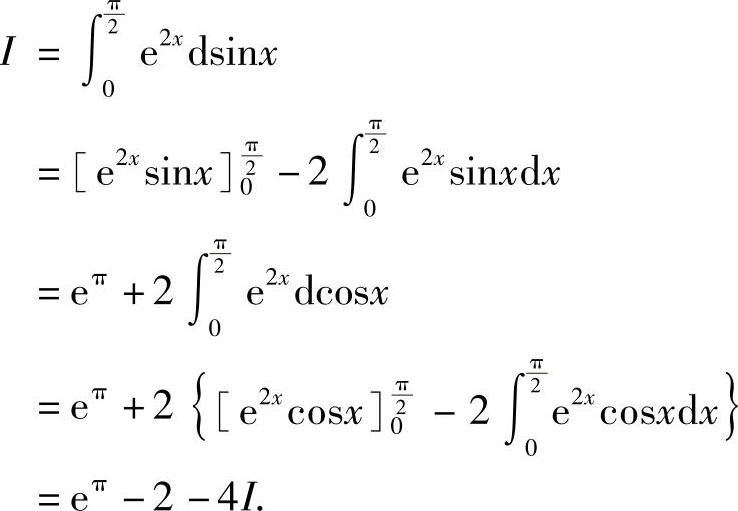
移项,解得
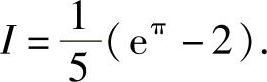
例11 求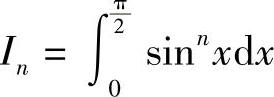 ,其中,n为非负整数.
,其中,n为非负整数.
解 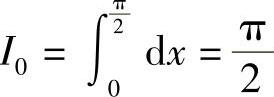 ,
, .当n≥2时,
.当n≥2时,
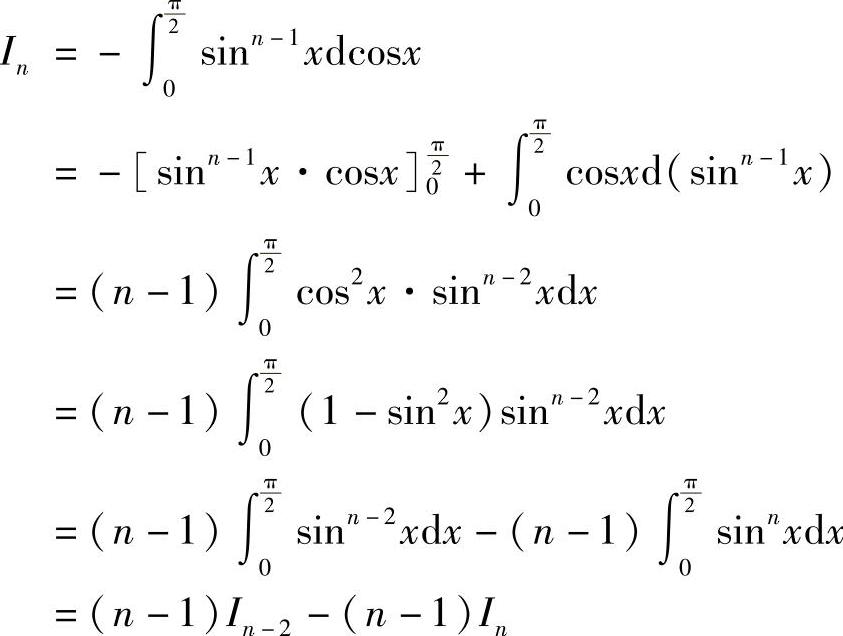
移项,得到In的递推公式
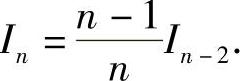
1)当n为偶数时,设n=2m,有
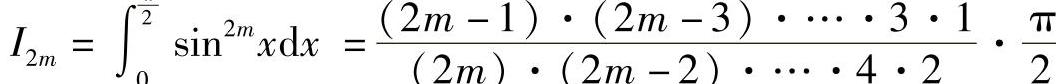
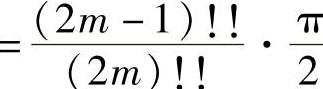 ;
;
2)当n为奇数时,设n=2m+1,有
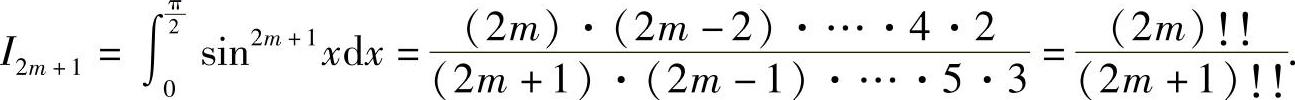
注:以后计算时可直接使用该公式,比如
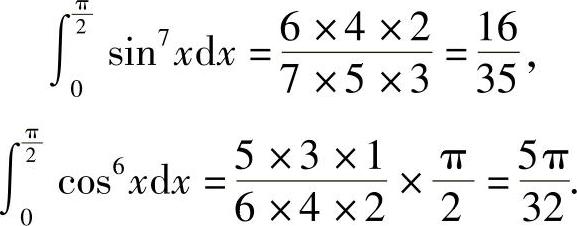
例12 设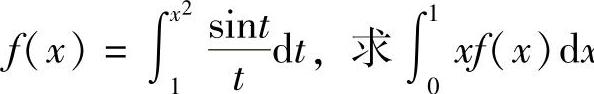 .
.
解