微分方程的基本概念
2026年01月14日
第一节 微分方程的基本概念
引例
例1 已知曲线上任一点的切线斜率等于该点横坐标的两倍,试建立其方程.
解 所求曲线应满足方程
例2 质量为m的物体只受重力的作用自由下落,试建立其路程s与时间t的关系.
解 把物体降落的铅垂线取作s轴,其指向朝下(朝向地心).设物体在t时刻的位置为s=s(t),加速度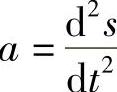 .
.
由牛顿第二定律F=ma,得

这是由著名科学家伽利略研究发现的,自由落体的重力加速度为常数g.
例3 某商品在t时刻的售价为P,社会对该商品的需求量和供给量分别是P的函数Q(P)、S(P),则在t时刻的价格P(t)对于时间t的变化率可以认为与该商品在同一时刻的超额需求量Q(t)-P(t)成正比(设比例系数为k),即有关系式(https://www.daowen.com)
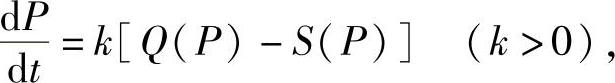
这就是商品的价格调整模型.
定义6.1 含有未知函数的导数(或微分)的方程称为微分方程.
微分方程中出现的未知函数的最高阶导数的阶数,叫做微分方程的阶.如方程(6-1)是一阶微分方程,方程(6-2)是二阶微分方程.
定义6.2 如果把某个函数代入微分方程,能使该方程成为恒等式,则称此函数为微分方程的解,即满足微分方程的函数叫做微分方程的解.
例如,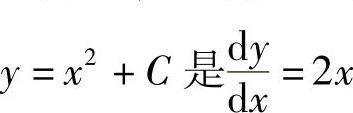 的解;
的解;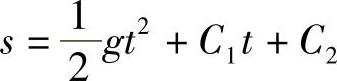 是
是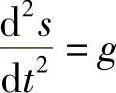 g的解.
g的解.
若微分方程解中所包含独立的任意常数的个数与对应的微分方程的阶数相同,这样的解称为微分方程的通解.
通过附加条件确定通解中的任意常数而得到的解称为微分方程的特解,这种附加条件称为初始条件.
例如,设方程未知函数为y=y(x),如果微分方程是一阶的,通常用来确定任意常数的条件是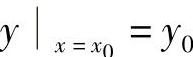 .其中,x0和y0是给定的数值;如果微分方程是二阶的,通常用来确定任意常数的条件是
.其中,x0和y0是给定的数值;如果微分方程是二阶的,通常用来确定任意常数的条件是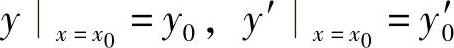 .
.
其中,x0、y0、y0′都是给定的数值.
