第一节  导数

第一节 导数

一、引例

1.做变速直线运动物体的速度

设物体沿横轴运动，路程s是时间t的函数s=f（t）.

如果物体的运动是匀速的，当时间由t₁改变到t₂时，在这一段时间里的平均速度定义为.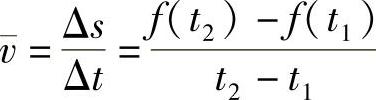

如果物体的运动是变速的，可以用它在每一时刻t₀的瞬时速度v（t₀）来更好地反映物体运动的状况.

当时间由t₀改变到t₀+Δt时，以平均速度v作为瞬时速度v（t₀）的近似值.显然Δt越接近0，平均速度v就越接近v（t₀），v在Δt趋于0时的极限就是物体在时刻t₀的瞬时速度的准确值，如下：

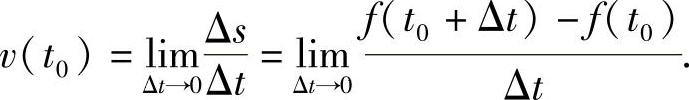
2.曲线的切线

设函数y=f（x）的图形如图2-1所示，过曲线y=f（x）上的一点P₀（x₀，y₀），作这条曲线的切线.在曲线上另取一点P（x₀+Δ_x，y₀+Δy），过这两点可以作一条割线P₀P，倾斜角为φ.

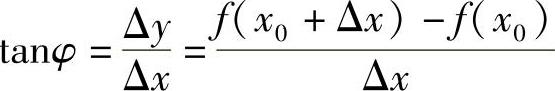
当Δx→0时，点P₀趋于P，割线P₀P的极限位置就是曲线过点P₀的切线P₀T，此时φ的极限为切线的倾斜角α，切线斜率为

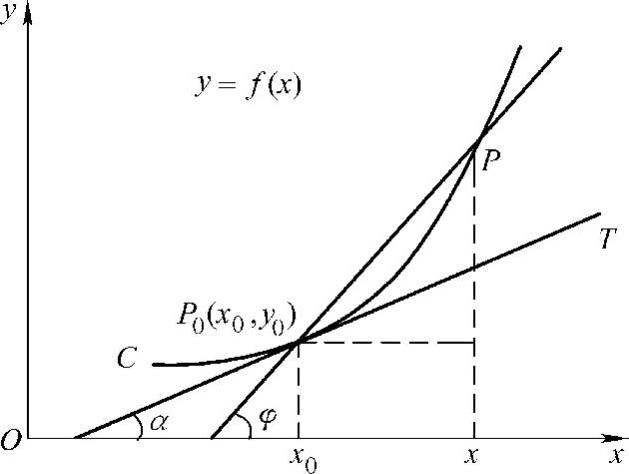
图2-1

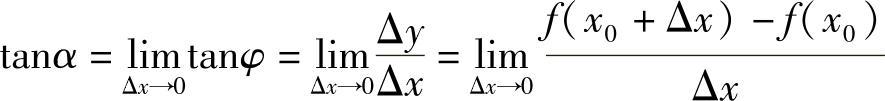
以上两个例子，具体含义不同，但是抽象的极限表达式却是一致的，称这种特殊的极限为函数的导数.

二、导数的概念

1.导数定义

定义2.1 设函数y=f（x）在点x₀的某个邻域内有定义，当自变量x在点x₀处取得增量Δx（Δx≠0）时，函数f（x）相应地取得增量Δy=f（x₀+Δx）-f（x₀）.如果极限

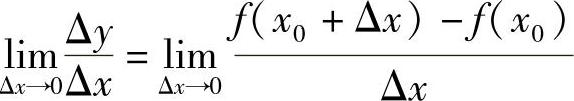
存在，则称函数f（x）在点x₀处可导，此极限称为函数f（x）在点x₀处的导数（或微商），记为f′（x₀）或.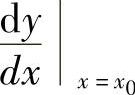

反之，若此极限不存在，则称函数f（x）在点x₀处不可导.

由此定义可知，第一个引例中的瞬时速度是路程s对时间t的导数，即

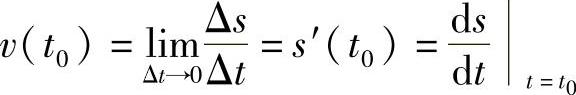
第2个引例中的切线斜率就是函数y对自变量x的导数，即

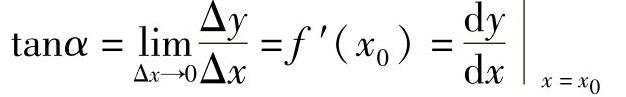
导数定义有时候也可以写成其他形式，如

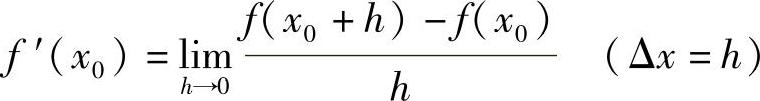
或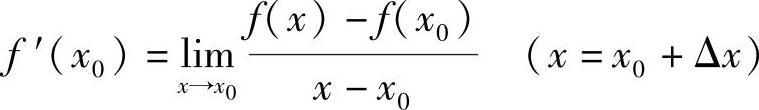

若函数f（x）在区间I可导，则对任意x∈I，都对应着一个导数值f′（x），则f′（x）也是区间I上的函数，称为函数f（x）在区间I上的导函数，简称为导数，记为f′（x），y′或.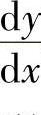

例1 求函数f（x）=C（C为常数）的导数.

解 .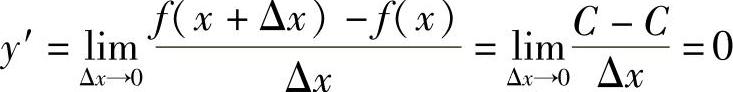

例2 求函数f（x）=xⁿ（n∈N+）在点x=a处的导数.

解 .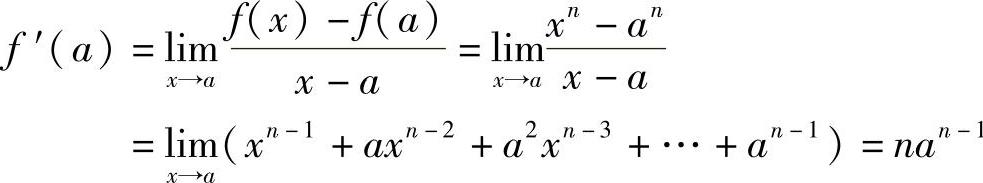

例3 求函数f（x）=x（x＞0）的导数.

解 由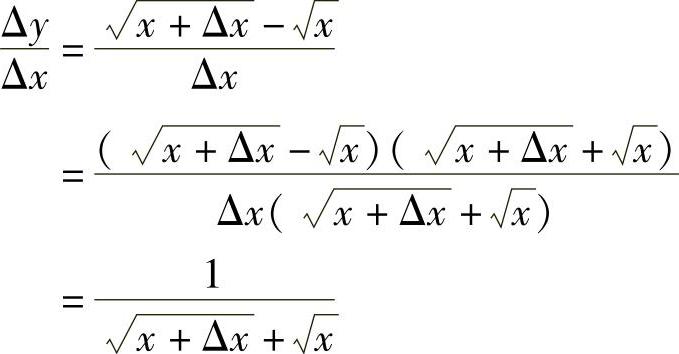

有.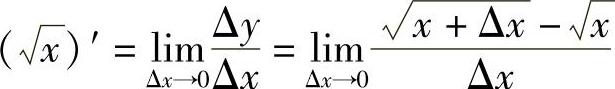

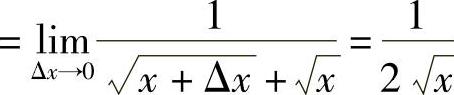可以证明，对任意的实数α，有（x^α）′=αx^α-1.

例4 求正弦函数f（x）=sinx的导数.

解 由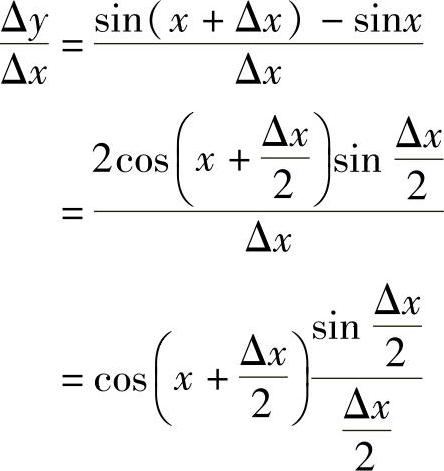

有.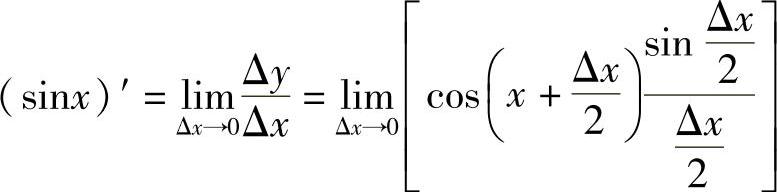

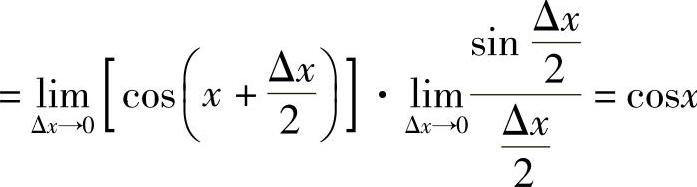同理，余弦函数cosx在定义域R内也可导，且

（cosx）′=-sinx.

例5 求对数函数f（x）=log_ax（a＞0，且a≠1，x＞0）在x的导数.

解 由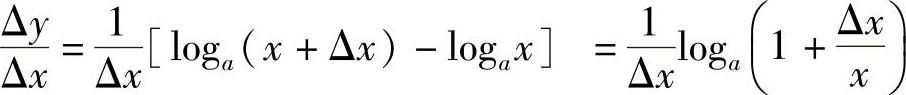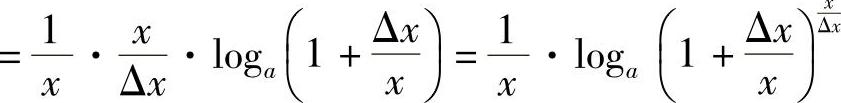(https://www.daowen.com)

有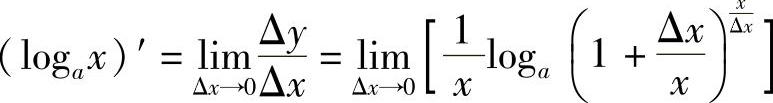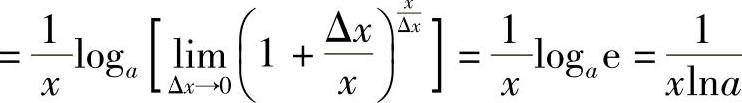，特别地，当a=e时，.

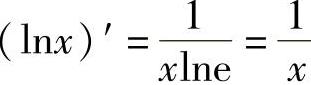2.导数的几何意义

由第二个引例可知，导数的几何意义（见图2-1）是：若曲线的方程是y=f（x），则曲线在点P₀（x₀，y₀）处的切线斜率就是f（x）在点x₀处的导数f′（x₀）.

由此可得曲线在点x₀处切线的点斜式方程为

y-y₀=f′（x₀）（x-x₀）.

法线方程为

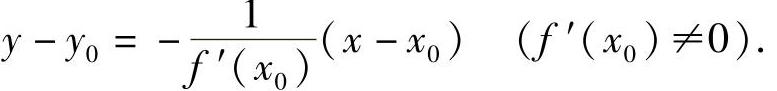
例6 求曲线y=x³在点P（x₀，y₀）处的切线与法线方程.

解 由于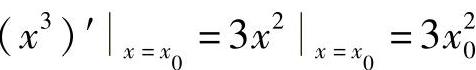，所以y=x³在P（x₀，y₀）处的切线方程为y-y₀=3x²₀（x-x₀）

当x₀≠0时，法线方程为

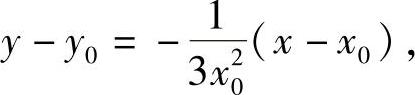
当x₀=0时，法线方程为x=0.

3.左、右导数

定义2.2 设函数y=f（x）在点x₀的某邻域内有定义，若左极限

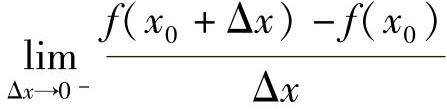
存在，则称函数f（x）在x₀左可导，并称此极限为函数f（x）在点x₀处的左导数，记作f_-′（x₀），即

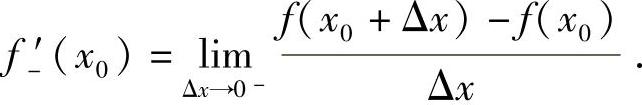
类似地，可以定义函数f（x）在点x₀的右可导及右导数

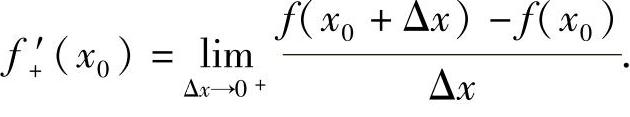
左、右导数统称为单侧导数.

若f（x）在（a，b）内处处可导，且在点x=a处右可导，在点x=b处左可导，就称f（x）在[a，b]上可导.

由极限存在的充要条件，可得

定理2.1 函数f（x）在点x₀处可导的充要条件是f（x）在x₀的左、右导数都存在且相等.

例7 讨论f（x）=x在点x=0处的连续性和可导性.

解 由题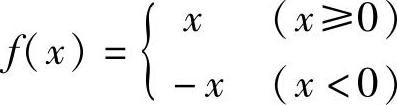，的图像如图2-2所示，因为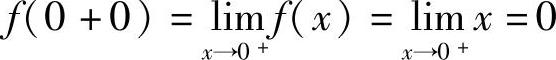

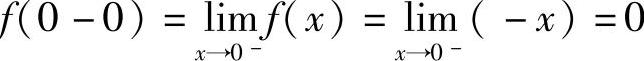
所以f（x）=|x|在点x=0连续；又因为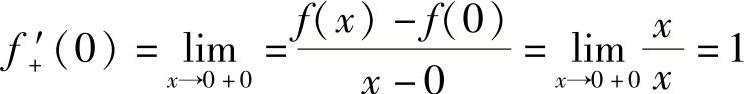

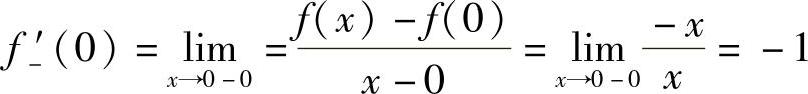
左、右导数不相等，所以在点x=0 f（x）=|x|不可导.

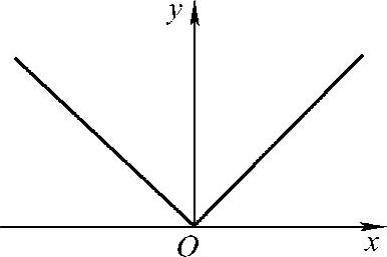
图2-2

三、可导与连续

定理2.2 若函数f（x）在x₀可导，则函数f（x）在x₀连续.

证 设在点x₀处自变量的增量是Δx，相应地函数的增量是

Δy=f（x₀+Δx）-f（x₀）

由.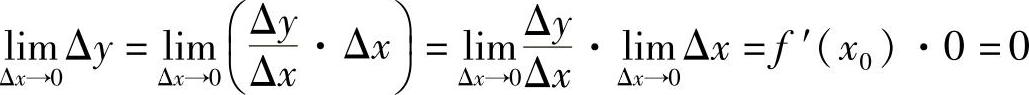

则函数f（x）在点x₀处连续.

本定理的逆命题不成立，例7就是一个反例.

例8 求常数a、b，使得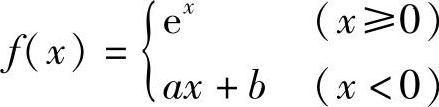在点x=0可导.

解 如果f（x）在点x=0可导，则该函数必在此点连续，故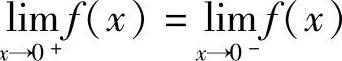=f（0），所以e⁰=a·0+b，则b=1.

如果f（x）在点x=0可导，则此点处的左、右导数必然存在且相等，

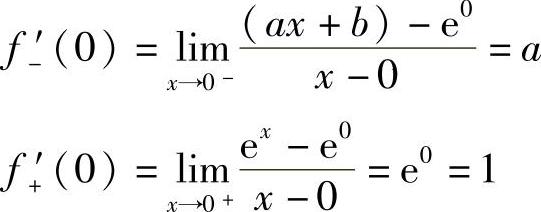
所以由f_-′（0）=f₊′（0），得a=1，此时f（x）在x=0点可导.

综上所述，所求常数为a=b=1.